|
|
7.2.1.4 ideal related functions (plural)
dim
- Gelfand-Kirillov dimension of basering modulo the ideal of leading terms (see dim (plural))
eliminate
- elimination of variables (see eliminate (plural))
intersect
- ideal intersection (see intersect (plural))
kbase
- vector space basis of basering modulo the leading ideal
(see kbase (plural))
lead
- leading terms of a set of generators (see lead)
lift
- lift-matrix (see lift (plural))
liftstd
- left Groebner basis and transformation matrix computation (see liftstd (plural))
maxideal
- generators of a power of the maximal ideal at 0 (see maxideal)
modulo
- represents
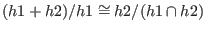 (see modulo (plural)) (see modulo (plural))
mres
- minimal free resolution of an ideal and a minimal set
of generators of the given ideal
(see mres (plural))
ncols
- number of columns (see ncols)
nres
- computes a free resolution of an ideal resp. module M which is
minimized from the second free module on (see nres (plural))
oppose
- creates an opposite ideal of a given ideal from the given ring into a basering (see oppose)
preimage
- preimage under a ring map (see preimage (plural))
quotient
- ideal quotient (see quotient (plural))
reduce
- left normal form with respect to a left Groebner basis (see reduce (plural))
simplify
- simplify a set of polynomials (see simplify)
size
- number of non-zero generators (see size)
slimgb
- left Groebner basis computation with slim technique (see slimgb (plural))
std
- left Groebner basis computation (see std (plural))
subst
- substitute a ring variable (see subst (plural))
syz
- computation of the first syzygy module (see syz (plural))
twostd
- two-sided Groebner basis computation (see twostd)
vdim
- vector space dimension of basering modulo the leading ideal (see vdim (plural))
|