|
|
7.5 Graded commutative algebras (SCA)
This section describes basic mathematical notions, definition, and a little bit the implementation of
the experimental non-commutative kernel extension SCA of SINGULAR
which improves performance of many algorithms in graded commutative algebras.
In order to improve performance of SINGULAR in specific non-commutative algebras
one can extend the internal implementation for them in a virtual-method-overloading-like manner.
At the moment graded commutative algebras (SCA) and in particular exterior algebras are implemented this way.
Note that grade commutative algebras require no special user actions apart from
defining an appropriate non-commutative GR-algebra in SINGULAR.
Upon doing that, the supper-commutative structure will be automatically detected and
special multiplication will be used.
Moreover, in most SCA-aware (e.g. std) algorithms special internal improvements will be used
(otherwise standard generic non-commutative implementations will be used).
All considered algebras are assumed to be associative
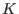 -algebras for some ground field -algebras for some ground field
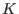 . .
- Definition
Polynomial graded commutative algebras are factors of tensor products of commutative algebras
with an exterior algebra over a ground field
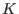 . .
These algebras can be naturally endowed with a
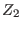 -grading, where anti-commutative algebra generators
have degree -grading, where anti-commutative algebra generators
have degree
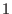 and commutative algebra generators (and naturally scalars) have degree and commutative algebra generators (and naturally scalars) have degree
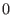 .
In this particular case they may be considered as super-commutative algebras. .
In this particular case they may be considered as super-commutative algebras.
- GR-algebra representation
A graded commutative algebra with
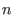 commutative and commutative and
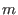 anti-commutative algebra generators can be represented
as factors of the following GR-algebra by some two-sided ideal: anti-commutative algebra generators can be represented
as factors of the following GR-algebra by some two-sided ideal:
- Distinctive features
Graded commutative algebras have zero divisors iff
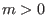 : :
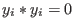 . .
Unlike other non-commutative algebras one may use any monomial ordering
where only the non-commutative variables are required to be global.
In particular, commutative variables are allowed to be local.
This means that one can work in tensor products of any commutative ring with an exterior algebra.
- Example of defining graded commutative algebras in SINGULAR
Given a commutative polynomial ring
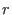 , super-commutative structure on it can be introduced as follows: , super-commutative structure on it can be introduced as follows:
| | LIB "nctools.lib";
ring r = 0,(a, b, x,y,z, Q, W),(lp(2), dp(3), Dp(2));
// Let us make variables x = var(3), ..., z = var(5) to be anti-commutative
// and add additionally a quotient ideal:
def S = superCommutative(3, 5, ideal(a*W + b*Q*x + z) ); setring S; S;
==> // coefficients: QQ
==> // number of vars : 7
==> // block 1 : ordering lp
==> // : names a b
==> // block 2 : ordering dp
==> // : names x y z
==> // block 3 : ordering Dp
==> // : names Q W
==> // block 4 : ordering C
==> // noncommutative relations:
==> // yx=-xy
==> // zx=-xz
==> // zy=-yz
==> // quotient ring from ideal
==> _[1]=xz
==> _[2]=bxyQ-yz
==> _[3]=aW+bxQ+z
==> _[4]=z2
==> _[5]=y2
==> _[6]=x2
ideal I = a*x*y + z*Q + b, y*Q + a; I;
==> I[1]=axy+b+zQ
==> I[2]=a+yQ
std(I); // Groebner basis is used here since > is global
==> _[1]=yQW-z
==> _[2]=yz
==> _[3]=b+zQ
==> _[4]=a+yQ
kill r;
// Let's do the same but this time with some local commutative variables:
ring r = 0,(a, b, x,y,z, Q, W),(dp(1), ds(1), lp(3), ds(2));
def S = superCommutative(3, 5, ideal(a*W + b*Q*x + z) ); setring S; S;
==> // ** redefining S (def S = superCommutative(3, 5, ideal(a*W + b*Q*x + z)\
); setring S; S;)
==> // coefficients: QQ
==> // number of vars : 7
==> // block 1 : ordering lp
==> // : names a
==> // block 2 : ordering ds
==> // : names b
==> // block 3 : ordering lp
==> // : names x y z
==> // block 4 : ordering ds
==> // : names Q W
==> // block 5 : ordering C
==> // noncommutative relations:
==> // yx=-xy
==> // zx=-xz
==> // zy=-yz
==> // quotient ring from ideal
==> _[1]=xz
==> _[2]=yz-bxyQ
==> _[3]=aW+z+bxQ
==> _[4]=x2
==> _[5]=y2
==> _[6]=z2
ideal I = a*x*y + z*Q + b, y*Q + a; I;
==> I[1]=axy+zQ+b
==> I[2]=a+yQ
std(I);
==> _[1]=yQW-z-bxQ
==> _[2]=zQ+b
==> _[3]=bx
==> _[4]=by
==> _[5]=bz
==> _[6]=b2
==> _[7]=a+yQ
|
See example of superCommutative from the library nctools.lib.
Reference: Ph.D thesis by Oleksandr Motsak (2010).
|