|
|
A.4.3 Polar curves
The polar curve of a hypersurface given by a polynomial
![$f\in k[x_1,\ldots,x_n,t]$](sing_399.png) with respect to with respect to
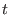 (we may consider (we may consider
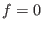 as a family of
hypersurfaces parametrized by as a family of
hypersurfaces parametrized by
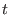 ) is defined as the Zariski
closure of ) is defined as the Zariski
closure of
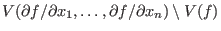 if this happens to be a curve. Some authors consider if this happens to be a curve. Some authors consider
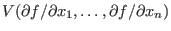 itself as polar curve. itself as polar curve.
We may consider projective hypersurfaces
(in 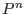 ),affine hypersurfaces
(in ),affine hypersurfaces
(in 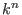 )or germs of hypersurfaces
(in )or germs of hypersurfaces
(in 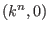 ),getting in this way
projective, affine or local polar curves. ),getting in this way
projective, affine or local polar curves.
Now let us compute this for a family of curves. We need the library
elim.lib for saturation and sing.lib for the singular
locus.
| | LIB "elim.lib";
LIB "sing.lib";
// Affine polar curve:
ring R = 0,(x,z,t),dp; // global ordering dp
poly f = z5+xz3+x2-tz6;
dim_slocus(f); // dimension of singular locus
==> 1
ideal j = diff(f,x),diff(f,z);
dim(std(j)); // dim V(j)
==> 1
dim(std(j+ideal(f))); // V(j,f) also 1-dimensional
==> 1
// j defines a curve, but to get the polar curve we must remove the
// branches contained in f=0 (they exist since dim V(j,f) = 1). This
// gives the polar curve set theoretically. But for the structure we
// may take either j:f or j:f^k for k sufficiently large. The first is
// just the ideal quotient, the second the iterated ideal quotient
// or saturation. In our case both coincide.
ideal q = quotient(j,ideal(f)); // ideal quotient
ideal qsat = sat(j,f)[1]; // saturation, proc from elim.lib
ideal sq = std(q);
dim(sq);
==> 1
// 1-dimensional, hence q defines the affine polar curve
//
// to check that q and qsat are the same, we show both inclusions, i.e.,
// both reductions must give the 0-ideal
size(reduce(qsat,sq));
==> 0
size(reduce(q,std(qsat)));
==> 0
qsat;
==> qsat[1]=12zt+3z-10
==> qsat[2]=5z2+12xt+3x
==> qsat[3]=144xt2+72xt+9x+50z
// We see that the affine polar curve does not pass through the origin,
// hence we expect the local polar "curve" to be empty
// ------------------------------------------------
// Local polar curve:
ring r = 0,(x,z,t),ds; // local ordering ds
poly f = z5+xz3+x2-tz6;
ideal j = diff(f,x),diff(f,z);
dim(std(j)); // V(j) 1-dimensional
==> 1
dim(std(j+ideal(f))); // V(j,f) also 1-dimensional
==> 1
ideal q = quotient(j,ideal(f)); // ideal quotient
q;
==> q[1]=1
// The local polar "curve" is empty, i.e., V(j) is contained in V(f)
// ------------------------------------------------
// Projective polar curve: (we need "sing.lib" and "elim.lib")
ring P = 0,(x,z,t,y),dp; // global ordering dp
poly f = z5y+xz3y2+x2y4-tz6;
// but consider t as parameter
dim_slocus(f); // projective 1-dimensional singular locus
==> 2
ideal j = diff(f,x),diff(f,z);
dim(std(j)); // V(j), projective 1-dimensional
==> 2
dim(std(j+ideal(f))); // V(j,f) also projective 1-dimensional
==> 2
ideal q = quotient(j,ideal(f));
ideal qsat = sat(j,f)[1]; // saturation, proc from elim.lib
dim(std(qsat));
==> 2
// projective 1-dimensional, hence q and/or qsat define the projective
// polar curve. In this case, q and qsat are not the same, we needed
// 2 quotients.
// Let us check both reductions:
size(reduce(qsat,std(q)));
==> 4
size(reduce(q,std(qsat)));
==> 0
// Hence q is contained in qsat but not conversely
q;
==> q[1]=12zty+3zy-10y2
==> q[2]=60z2t-36xty-9xy-50zy
==> q[3]=12xty2+5z2y+3xy2
==> q[4]=z3y+2xy3
qsat;
==> qsat[1]=12zt+3z-10y
==> qsat[2]=12xty+5z2+3xy
==> qsat[3]=144xt2+72xt+9x+50z
==> qsat[4]=z3+2xy2
//
// Now consider again the affine polar curve,
// homogenize it with respect to y (deg t=0) and compare:
// affine polar curve:
ideal qa = 12zt+3z-10,5z2+12xt+3x,-144xt2-72xt-9x-50z;
// homogenized:
ideal qh = 12zt+3z-10y,5z2+12xyt+3xy,-144xt2-72xt-9x-50z;
size(reduce(qh,std(qsat)));
==> 0
size(reduce(qsat,std(qh)));
==> 0
// both ideals coincide
|
|