|
|
C.5 Gauss-Manin connection
Let
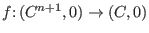 be a complex isolated hypersurface singularity given by a polynomial with algebraic coefficients which we also denote by be a complex isolated hypersurface singularity given by a polynomial with algebraic coefficients which we also denote by 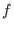 .
Let .
Let
![$O=C[x_0,\ldots,x_n]_{(x_0,\ldots,x_n)}$](sing_602.png) be the local ring at the origin and be the local ring at the origin and 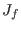 the Jacobian ideal of the Jacobian ideal of 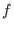 . .
A Milnor representative of 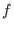 defines a differentiable fibre bundle over the punctured disc with fibres of homotopy type of defines a differentiable fibre bundle over the punctured disc with fibres of homotopy type of 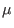 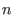 -spheres.
The -spheres.
The 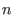 -th cohomology bundle is a flat vector bundle of dimension -th cohomology bundle is a flat vector bundle of dimension 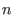 and carries a natural flat connection with covariant derivative and carries a natural flat connection with covariant derivative 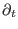 .
The monodromy operator is the action of a positively oriented generator of the fundamental group of the punctured disc on the Milnor fibre.
Sections in the cohomology bundle of moderate growth at .
The monodromy operator is the action of a positively oriented generator of the fundamental group of the punctured disc on the Milnor fibre.
Sections in the cohomology bundle of moderate growth at 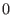 form a regular form a regular
![$D=C\{t\}[\partial_t]$](sing_606.png) -module -module 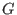 , the Gauss-Manin connection. , the Gauss-Manin connection.
By integrating along flat multivalued families of cycles, one can consider fibrewise global holomorphic differential forms as elements of 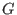 .
This factors through an inclusion of the Brieskorn lattice .
This factors through an inclusion of the Brieskorn lattice
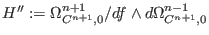 in in 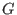 . .
The 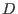 -module structure defines the V-filtration -module structure defines the V-filtration 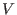 on on 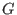 by by
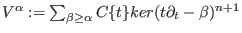 .
The Brieskorn lattice defines the Hodge filtration .
The Brieskorn lattice defines the Hodge filtration 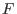 on on 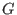 by by
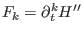 which comes from the mixed Hodge structure on the Milnor fibre.
Note that which comes from the mixed Hodge structure on the Milnor fibre.
Note that 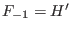 . .
The induced V-filtration on the Brieskorn lattice determines the singularity spectrum  by by
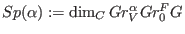 .
The spectrum consists of .
The spectrum consists of 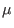 rational numbers rational numbers
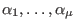 such that such that
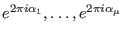 are the eigenvalues of the monodromy.
These spectral numbers lie in the open interval are the eigenvalues of the monodromy.
These spectral numbers lie in the open interval 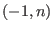 , symmetric about the midpoint , symmetric about the midpoint 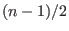 . .
The spectrum is constant under 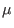 -constant deformations and has the following semicontinuity property:
The number of spectral numbers in an interval -constant deformations and has the following semicontinuity property:
The number of spectral numbers in an interval ![$(a,a+1]$](sing_618.png) of all singularities of a small deformation of of all singularities of a small deformation of 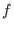 is greater than or equal to that of f in this interval.
For semiquasihomogeneous singularities, this also holds for intervals of the form is greater than or equal to that of f in this interval.
For semiquasihomogeneous singularities, this also holds for intervals of the form 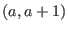 . .
Two given isolated singularities 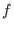 and and 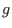 determine two spectra and from these spectra we get an integer.
This integer is the maximal positive integer determine two spectra and from these spectra we get an integer.
This integer is the maximal positive integer 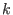 such that the semicontinuity holds for the spectrum of such that the semicontinuity holds for the spectrum of 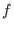 and and 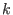 times the spectrum of times the spectrum of 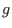 .
These numbers give bounds for the maximal number of isolated singularities of a specific type on a hypersurface .
These numbers give bounds for the maximal number of isolated singularities of a specific type on a hypersurface 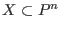 of degree of degree 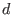 :
such a hypersurface has a smooth hyperplane section, and the complement is a small deformation of a cone over this hyperplane section.
The cone itself being a :
such a hypersurface has a smooth hyperplane section, and the complement is a small deformation of a cone over this hyperplane section.
The cone itself being a 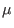 -constant deformation of -constant deformation of
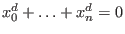 , the singularities are bounded by the spectrum of , the singularities are bounded by the spectrum of
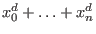 . .
Using the library gmssing.lib one can compute the monodromy, the V-fitration on 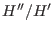 , and the spectrum. , and the spectrum.
Let us consider as an example
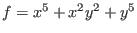 .
First, we compute a matrix .
First, we compute a matrix
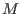 such that such that
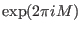 is a monodromy matrix of is a monodromy matrix of
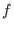 and the Jordan normal form of and the Jordan normal form of
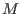 : :
| | LIB "mondromy.lib";
ring R=0,(x,y),ds;
poly f=x5+x2y2+y5;
matrix M=monodromyB(f);
print(M);
==> 11/10,0, 0, 0, 0, 0,-1/4,0, 0, 0, 0,
==> 0, 13/10,0, 0, 0, 0,0, 15/8,0, 0, 0,
==> 0, 0, 13/10,0, 0, 0,0, 0, 15/8,0, 0,
==> 0, 0, 0, 11/10,-1/4,0,0, 0, 0, 0, 0,
==> 0, 0, 0, 0, 9/10,0,0, 0, 0, 0, 0,
==> 0, 0, 0, 0, 0, 1,0, 0, 0, 0, 3/5,
==> 0, 0, 0, 0, 0, 0,9/10,0, 0, 0, 0,
==> 0, 0, 0, 0, 0, 0,0, 7/10,0, 0, 0,
==> 0, 0, 0, 0, 0, 0,0, 0, 7/10,0, 0,
==> 0, 0, 0, 0, 0, 0,0, 0, 0, 1, -2/5,
==> 0, 0, 0, 0, 0, 0,0, 0, 0, 5/8,0
|
Now, we compute the V-fitration on
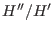 and the spectrum: and the spectrum:
| | LIB "gmssing.lib";
ring R=0,(x,y),ds;
poly f=x5+x2y2+y5;
list l=vfilt(f);
print(l[1]); // spectral numbers
==> -1/2,
==> -3/10,
==> -1/10,
==> 0,
==> 1/10,
==> 3/10,
==> 1/2
print(l[2]); // corresponding multiplicities
==> 1,
==> 2,
==> 2,
==> 1,
==> 2,
==> 2,
==> 1
print(l[3]); // vector space of i-th graded part
==> [1]:
==> _[1]=gen(11)
==> [2]:
==> _[1]=gen(10)
==> _[2]=gen(6)
==> [3]:
==> _[1]=gen(9)
==> _[2]=gen(4)
==> [4]:
==> _[1]=gen(5)
==> [5]:
==> _[1]=gen(3)
==> _[2]=gen(8)
==> [6]:
==> _[1]=gen(2)
==> _[2]=gen(7)
==> [7]:
==> _[1]=gen(1)
print(l[4]); // monomial vector space basis of H''/s*H''
==> y5,
==> y4,
==> y3,
==> y2,
==> xy,
==> y,
==> x4,
==> x3,
==> x2,
==> x,
==> 1
print(l[5]); // standard basis of Jacobian ideal
==> 2x2y+5y4,
==> 5x5-5y5,
==> 2xy2+5x4,
==> 10y6+25x3y4
|
Here l[1] contains the spectral numbers, l[2] the corresponding multiplicities, l[3] a
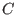 -basis of the V-filtration on -basis of the V-filtration on
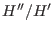 in terms of the monomial basis of in terms of the monomial basis of
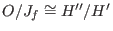 in in l[4] (seperated by degree).
If the principal part of 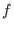 is is 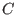 -nondegenerate, one can compute the spectrum using the library spectrum.lib.
In this case, the V-filtration on -nondegenerate, one can compute the spectrum using the library spectrum.lib.
In this case, the V-filtration on 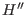 coincides with the Newton-filtration on coincides with the Newton-filtration on 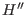 which allows to compute the spectrum more efficiently. which allows to compute the spectrum more efficiently.
Let us calculate one specific example, the maximal number
of triple points of type
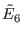 on a surface on a surface 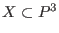 of degree seven.
This calculation can be done over the rationals.
We choose a local ordering on of degree seven.
This calculation can be done over the rationals.
We choose a local ordering on
![$Q[x,y,z]$](sing_37.png) . Here we take the
negative degree lexicographical ordering, in SINGULAR denoted by . Here we take the
negative degree lexicographical ordering, in SINGULAR denoted by ds:
| | ring r=0,(x,y,z),ds;
LIB "spectrum.lib";
poly f=x^7+y^7+z^7;
list s1=spectrumnd( f );
s1;
==> [1]:
==> _[1]=-4/7
==> _[2]=-3/7
==> _[3]=-2/7
==> _[4]=-1/7
==> _[5]=0
==> _[6]=1/7
==> _[7]=2/7
==> _[8]=3/7
==> _[9]=4/7
==> _[10]=5/7
==> _[11]=6/7
==> _[12]=1
==> _[13]=8/7
==> _[14]=9/7
==> _[15]=10/7
==> _[16]=11/7
==> [2]:
==> 1,3,6,10,15,21,25,27,27,25,21,15,10,6,3,1
|
The command spectrumnd(f) computes the spectrum of
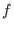 and
returns a list with six entries:
The Milnor number and
returns a list with six entries:
The Milnor number
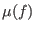 , the geometric genus , the geometric genus 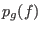 and the number of different spectrum numbers.
The other three entries are of type and the number of different spectrum numbers.
The other three entries are of type intvec.
They contain the numerators, denominators and
multiplicities of the spectrum numbers. So
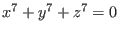 has Milnor number 216 and geometrical
genus 35. Its spectrum consists of the 16 different rationals has Milnor number 216 and geometrical
genus 35. Its spectrum consists of the 16 different rationals
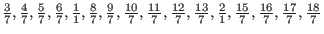
appearing with multiplicities
1,3,6,10,15,21,25,27,27,25,21,15,10,6,3,1.
The singularities of type 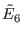 form a form a
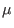 -constant one parameter family given by -constant one parameter family given by
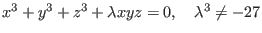 .Therefore they have all the same spectrum, which we compute
for .Therefore they have all the same spectrum, which we compute
for
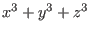 . .
| | poly g=x^3+y^3+z^3;
list s2=spectrumnd(g);
s2;
==> [1]:
==> 8
==> [2]:
==> 1
==> [3]:
==> 4
==> [4]:
==> 1,4,5,2
==> [5]:
==> 1,3,3,1
==> [6]:
==> 1,3,3,1
|
Evaluating semicontinuity is very easy:
This tells us that there are at most 18 singularities of type
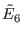 on a septic in on a septic in 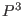 . But . But 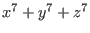 is semiquasihomogeneous (sqh), so we can also apply the stronger
form of semicontinuity: is semiquasihomogeneous (sqh), so we can also apply the stronger
form of semicontinuity:
| | semicontsqh(s1,s2);
==> 17
|
So in fact a septic has at most 17 triple points of type
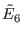 . .
Note that spectrumnd(f) works only if
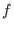 has a nondegenerate
principal part. In fact has a nondegenerate
principal part. In fact spectrumnd will detect a degenerate
principal part in many cases and print out an error message.
However if it is known in advance that
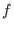 has nondegenerate
principal part, then the spectrum may be computed much faster
using has nondegenerate
principal part, then the spectrum may be computed much faster
using spectrumnd(f,1).
|