|
|
7.3.21 preimage (plural)
Syntax:
preimage ( ring_name, map_name, ideal_name )
preimage ( ring_name, ideal_expression, ideal_name )
Type:
- ideal
Purpose:
- returns the preimage of an ideal under a given map.
The second argument has to be a map from the basering to the given ring
(or an ideal defining such a map),
and the ideal has to be an ideal in the given ring.
Note:
- To compute the kernel of a map, the preimage of zero has to be determined.
Hence there is no special command for computing the kernel of a map in
PLURAL.
Remark:
- In the non-commutative case, it is implemented only for maps
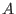 -> ->
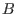 , where , where
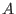 is a commutative ring. is a commutative ring.
Example:
| | LIB "ncalg.lib";
ring R = 0,a,dp;
def Usl2 = makeUsl2();
setring Usl2;
poly C = 4*e*f+h^2-2*h;
// C is a central element of U(sl2)
ideal I = e^3, f^3, h^3-4*h;
ideal Z = 0; // zero
ideal J = twostd(I); // two-sided GB
ideal K = std(I); // left GB
map Phi = R,C; // phi maps a (in R) to C (in U(sl2))
setring R;
ideal PreJ = preimage(Usl2,Phi,J);
// the central character of J
PreJ;
==> PreJ[1]=a2-8a
factorize(PreJ[1],1);
==> _[1]=a
==> _[2]=a-8
// hence, there are two simple characters for J
ideal PreK = preimage(Usl2,Phi,K);
// the central character of K
PreK;
==> PreK[1]=a3-32a2+192a
factorize(PreK[1],1);
==> _[1]=a
==> _[2]=a-24
==> _[3]=a-8
// hence, there are three simple characters for K
preimage(Usl2, Phi, Z); // kernel pf phi
==> _[1]=0
|
See
ideal (plural);
map (plural);
ring (plural).
|