7.9.4 Letterplace correspondence
The name letteplace has been inspired by the work of Rota and, independently, Feynman.
Already Feynman and Rota encoded
the monomials (words) of the free algebra
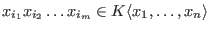 via the double-indexed letterplace
(that is encoding the letter (= variable) and its place in the word) monomials
via the double-indexed letterplace
(that is encoding the letter (= variable) and its place in the word) monomials
![$x(i_1 \vert 1) x(i_2 \vert 2) \dots x(i_m \vert m) \in K[X\times N]$](sing_388.png) , where , where
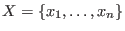 and
and 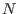 is the semigroup of natural numbers, starting with 1 as the first possible place.
Note, that the letterplace algebra is the semigroup of natural numbers, starting with 1 as the first possible place.
Note, that the letterplace algebra ![$K[X \times N]$](sing_391.png) is an infinitely generated commutative polynomial is an infinitely generated commutative polynomial 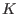 -algebra.
Since -algebra.
Since
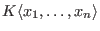 is not Noetherian, it is common to perform the computations with
its ideals and modules up to a given degree bound. is not Noetherian, it is common to perform the computations with
its ideals and modules up to a given degree bound.
Subject to the given degree (length) bound 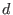 , the truncated letterplace algebra , the truncated letterplace algebra
![$K[X\times (1, ..., d)]$](sing_393.png) is finitely generated commutative polynomial is finitely generated commutative polynomial 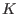 -algebra. -algebra.
In [LL09] a natural shifting on letterplace polynomials was introduced and used.
Indeed, there is 1-to-1 correspondence between two-sided ideals
of a free algebra and so-called letterplace ideals in the letterplace algebra,
see [LL09], [LL13], [LSS13] and [L14] for details.
Note, that first this correspondence was established for graded ideals.
All the computations take place in the letterplace algebra.
A letterplace monomial of length
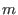 is a monomial of a letterplace algebra,
such that its is a monomial of a letterplace algebra,
such that its
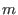 places are exactly 1,2,..., places are exactly 1,2,...,
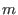 .
In particular, such monomials are multilinear with respect to places (i.e.
no place, smaller than the length is omitted or filled more than with one letter).
A letterplace polynomial is an element of the .
In particular, such monomials are multilinear with respect to places (i.e.
no place, smaller than the length is omitted or filled more than with one letter).
A letterplace polynomial is an element of the
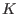 -vector space,
spanned by letterplace monomials. A letterplace ideal is generated by letterplace
polynomials subject to two kind of operations: -vector space,
spanned by letterplace monomials. A letterplace ideal is generated by letterplace
polynomials subject to two kind of operations:
the
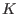 -algebra operations of the letterplace algebra and simultaneous shifting of places by any natural number -algebra operations of the letterplace algebra and simultaneous shifting of places by any natural number 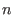 . .
|