|
|
5.1.85 luinverse
Syntax:
luinverse ( matrix_expression )
Type:
- matrix
Syntax:
luinverse ( matrix_expression, matrix_expression, matrix_expression )
Type:
- matrix
Purpose:
- Computes the inverse of a matrix A, if A is invertible.
The matrix A must be given either directly, or by its LU-decomposition.
In the latter case, three matrices P, L, and U are expected, in this order,
which satisfy
- P * A = L * U,
- P is an (m x m) permutation matrix, i.e., its rows/columns form the
standard basis of K^m,
- L is an (m x m) matrix in lower triangular form with all diagonal
entries equal to 1, and
- U is an (m x m) matrix in upper row echelon form.
Then, the inverse of A exists if and only if U is invertible, and one has
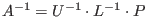 ,since P is self-inverse. ,since P is self-inverse.
In the case of A being given directly, luinverse first computes its
LU-decomposition, and then proceeds as in the case when P, L, and U are
provided.
list L=luinverse(A); fills the list L with either one entry = 0
(signaling that A is not invertible), or with the two entries
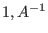 .Thus, in either case the user may first check the condition .Thus, in either case the user may first check the condition
L[1]==1 to find out whether A is invertible.
Note:
- The method will give a warning for any non-quadratic matrix A.
Example:
| | ring r=0,(x),dp;
matrix A[3][3]=1,2,3,1,1,1,2,2,1;
list L = luinverse(A);
if (L[1] == 1)
{
print(L[2]);
"----- next should be the (3 x 3)-unit matrix:";
print(A*L[2]);
}
==> -1,4, -1,
==> 1, -5,2,
==> 0, 2, -1
==> ----- next should be the (3 x 3)-unit matrix:
==> 1,0,0,
==> 0,1,0,
==> 0,0,1
|
See
ludecomp.
|