|
|
7.2.2.3 map (plural) operations
( )
- composition of maps. If, for example,
f and g are maps,
then f(g) is a map expression giving the composition
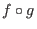 of f and g, provided the target ring of g is the basering of f.
- map_expression
[ int_expressions ]
- is a map entry (the image of the corresponding variable)
Example:
| | LIB "ncalg.lib";
def Usl2 = makeUsl2(); // this algebra is U(sl_2)
setring Usl2;
map F = Usl2, f, e, -h; // involutive endomorphism of U(sl_2)
F;
==> F[1]=f
==> F[2]=e
==> F[3]=-h
map G = F(F);
G;
==> G[1]=e
==> G[2]=f
==> G[3]=h
poly p = (f+e*h)^2 + 3*h-e;
p;
==> e2h2+2e2h+2efh-2ef+f2-h2-e+3h
F(p);
==> f2h2-2efh-2f2h+e2-2ef+h2-f-h
G(p);
==> e2h2+2e2h+2efh-2ef+f2-h2-e+3h
(G(p) == p); // G is the identity
==> 1
|
|
Online Manual
