|
|
7.7.2 Example of use of LETTERPLACE over Z
Consider the following paradigmatic example:
| | LIB "freegb.lib";
ring r = integer,(x,y),Dp;
ring R = freeAlgebra(r,5); // length bound is 5
ideal I = 2*x, 3*y;
I = twostd(I);
print(matrix(I)); // pretty prints the generators
==> 3*y,2*x,y*x,x*y
|
As we can see, over
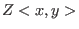 the ideal the ideal
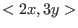 has
a finite Groebner basis and indeed has
a finite Groebner basis and indeed
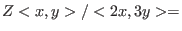
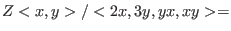
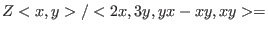
![$Z[x,y]/<2x,3y,xy>$](sing_1021.png) holds. holds.
Now, we analyze the same ideal in the ring with one more variable
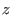 : :
| | LIB "freegb.lib";
ring r = integer,(x,y,z),Dp;
ring R = freeAlgebra(r,5,2); // length bound is 5
ideal I = 2*x, 3*y;
I = twostd(I);
print(matrix(I)); // pretty prints the generators
==> 3*y,2*x,y*x,x*y,y*z*x,x*z*y,y*z*z*x,x*z*z*y,y*z*z*z*x,x*z*z*z*y
|
Now we see, that this Groebner basis is potentially infinite and
the following argument delivers a proof. Namely,
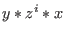 and and
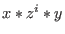 are present in the ideal for all are present in the ideal for all
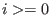 .
How can we do this? We wish to express .
How can we do this? We wish to express
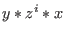 and and
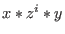 via the original generators: via the original generators:
| | LIB "freegb.lib";
ring r = integer,(x,y,z),Dp;
ring R = freeAlgebra(r,5,2); // length bound is 5, rank of the free bimodule is 2
ideal I = 2*x, 3*y;
matrix T1 = lift(I, ideal(y*z*x,x*z*y));
print(T1);
==> -y*z*ncgen(1),-ncgen(1)*z*y,
==> ncgen(2)*z*x, x*z*ncgen(2)
-y*z*I[1] + I[2]*z*x; // gives y*z*x
==> y*z*x
matrix T2 = lift(I, ideal(y*z^2*x,x*z^2*y));
print(T2);
==> -y*z*z*ncgen(1),-ncgen(1)*z*z*y,
==> ncgen(2)*z*z*x, x*z*z*ncgen(2)
-y*z^2*I[1] + I[2]*z^2*x; // gives y*z^2*x
==> y*z*z*x
|
The columns of matrices, returned by lift, encode the presentation of new
elements in terms of generators. From this we conjecture, that in particular
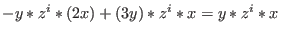 holds for all holds for all
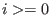
and indeed, confirm it via a routine computation by hands.
Comparing computations over Q with computations over Z.
In the next example, we first compute over
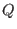 and a bit later
compare the result with computations over and a bit later
compare the result with computations over
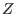 . .
| | LIB "freegb.lib"; // initialization of free algebras
ring r = 0,(z,y,x),Dp; // degree left lex ord on z>y>x
ring R = freeAlgebra(r,7); // length bound is 7
ideal I = y*x - 3*x*y - 3*z, z*x - 2*x*z +y, z*y-y*z-x;
option(redSB); option(redTail); // for minimal reduced GB
option(intStrategy); // avoid divisions by coefficients
ideal J = twostd(I); // compute a two-sided GB of I
J; // prints generators of J
==> J[1]=4*x*y+3*z
==> J[2]=3*x*z-y
==> J[3]=4*y*x-3*z
==> J[4]=2*y*y-3*x*x
==> J[5]=2*y*z+x
==> J[6]=3*z*x+y
==> J[7]=2*z*y-x
==> J[8]=3*z*z-2*x*x
==> J[9]=4*x*x*x+x
LIB "fpadim.lib"; // load the library for K-dimensions
lpMonomialBasis(7,0,J); // compute all monomials
==> _[1]=1
==> _[2]=z
==> _[3]=y
==> _[4]=x
==> _[5]=x*x
// of length up to 7 in Q<x,y,z>/J
|
As we see, we obtain a nice finite Groebner basis J.
Moreover, from the form of its leading monomials, we conjecture that
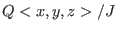 is finite dimensional is finite dimensional
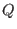 -vector space.
We check it with -vector space.
We check it with lpMonomialBasis and obtain an affirmative answer.
Now, for doing similar computations over
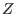 one needs to change
only the initialization of the ring, the rest stays the same one needs to change
only the initialization of the ring, the rest stays the same
| | LIB "freegb.lib"; // initialization of free algebras
ring r = integer,(z,y,x),Dp; // Z and deg left lex ord on z>y>x
ring R = freeAlgebra(r,7); // length bound is 7
ideal I = y*x - 3*x*y - 3*z, z*x - 2*x*z +y, z*y-y*z-x;
option(redSB); option(redTail); // for minimal reduced GB
option(intStrategy); // avoid divisions by coefficients
ideal J = twostd(I); // compute a two-sided GB of I
J; // prints generators of J
==> J[1]=12*x*y+9*z
==> J[2]=9*x*z-3*y
==> J[3]=y*x-3*x*y-3*z
==> J[4]=6*y*y-9*x*x
==> J[5]=6*y*z+3*x
==> J[6]=z*x-2*x*z+y
==> J[7]=z*y-y*z-x
==> J[8]=3*z*z+2*y*y-5*x*x
==> J[9]=6*x*x*x-3*y*z
==> J[10]=4*x*x*y+3*x*z
==> J[11]=3*x*x*z+3*x*y+3*z
==> J[12]=2*x*y*y+75*x*x*x+39*y*z+39*x
==> J[13]=3*x*y*z+3*y*y-3*x*x
==> J[14]=2*y*y*y+x*x*y+3*x*z
==> J[15]=2*x*x*x*x+y*y-x*x
==> J[16]=2*x*x*x*y+3*y*y*z+3*x*y+3*z
==> J[17]=x*x*y*z+x*y*y-x*x*x
==> J[18]=x*y*y*z-y*y*y+x*x*y
==> J[19]=x*x*x*x*x-y*y*y*z-x*y*y+x*x*x
==> J[20]=x*x*x*x*z+x*x*x*y+2*y*y*z+x*x*z+3*x*y+3*z
==> J[21]=x*y*y*y*z-y*y*y*y+x*x*x*x-y*y+x*x
==> J[22]=y*y*y*z*z-x*x*x*x*y
==> J[23]=x*y*y*y*y*z-y*y*y*y*y+x*x*y*y*y
==> J[24]=x*y*y*y*y*y*z-y*y*y*y*y*y+x*x*x*x*y*y+y*y*y*y+x*x*x*x+2*y*y-2*x*x
|
The output has plenty of elements in each degree (which is the same as length
because of the degree ordering), what hints at potentially infinite Groebner basis.
Indeed, one can show that for every
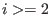 the ideal the ideal
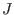 contains an element
with the leading monomial contains an element
with the leading monomial
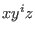 . .
|