7.9.4 Bimodules and syzygies and lifts
Let
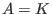
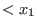 ,..., ,...,
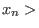 be the free algebra.
A free bimodule of rank be the free algebra.
A free bimodule of rank
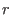 over over
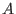 is is
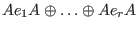 ,where ,where
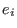 are the generators of the free bimodule. are the generators of the free bimodule.
NOTE: these
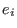 are freely non-commutative with respect to
elements of are freely non-commutative with respect to
elements of
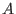 except constants from the ground field except constants from the ground field
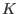 . .
The free bimodule of rank 1
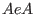 surjects onto the algebra surjects onto the algebra
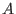 itself.
A two-sided ideal of the algebra itself.
A two-sided ideal of the algebra
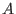 can be converted to a subbimodule of can be converted to a subbimodule of
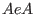 . .
The syzygy bimodule or even module of bisyzygies
of the given finitely generated subbimodule
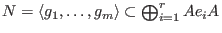 is the kernel of the natural homomorphism of is the kernel of the natural homomorphism of
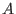 -bimodules -bimodules
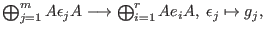 that is that is
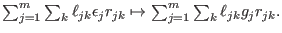
The syzygy bimodule is in general not finitely generated.
Therefore as a bimodule, both the set of generators of the
syzygy bimodule and its Groebner basis
are computed up to a specified length bound.
Given a subbimodule
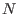 of a bimodule of a bimodule
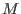 , the lift(ing) process
returns a matrix, which encodes the expression of generators , the lift(ing) process
returns a matrix, which encodes the expression of generators
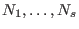 in terms of generators of
in terms of generators of
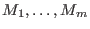 like this: like this:
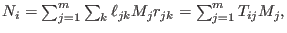
where T_ij are elements from the enveloping algebra
 encoded as elements of the free bimodule of rank encoded as elements of the free bimodule of rank
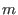 ,
namely by using the non-commutative generators of the
free bimodule which we call ,
namely by using the non-commutative generators of the
free bimodule which we call ncgen.
|