|
|
B.2.5 Module orderings
SINGULAR offers also orderings on the set of "monomials"
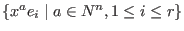 in Loc in Loc ![$K[x]^r$](sing_533.png) = Loc = Loc
![$K[x]e_1
+ \ldots +$](sing_534.png) Loc Loc ![$K[x]e_r$](sing_535.png) , where , where
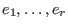 denote the canonical
generators of Loc denote the canonical
generators of Loc ![$K[x]^r$](sing_533.png) , the r-fold direct sum of Loc , the r-fold direct sum of Loc ![$K[x]$](sing_512.png) .
(The function gen(i) yields .
(The function gen(i) yields 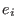 ). ).
We have two possibilities: either to give priority to the component of a
vector in
Loc ![$K[x]^r$](sing_533.png) or (which is the default in SINGULAR) to give priority
to the coefficients.
The orderings or (which is the default in SINGULAR) to give priority
to the coefficients.
The orderings (<,c) and (<,C) give priority to the
coefficients; whereas
(c,<) and (C,<) give priority to the components.
Let < be any of the monomial orderings of
Loc ![$K[x]$](sing_512.png) as above. as above.
- (<,C):
-
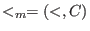 denotes the module ordering (giving priority to the coefficients): denotes the module ordering (giving priority to the coefficients):
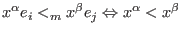 or ( or (
 and and 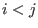 ). ).
Example:
| | ring r = 0, (x,y,z), ds;
// the same as ring r = 0, (x,y,z), (ds, C);
[x+y2,z3+xy];
==> x*gen(1)+xy*gen(2)+y2*gen(1)+z3*gen(2)
[x,x,x];
==> x*gen(3)+x*gen(2)+x*gen(1)
|
- (C,<):
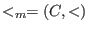 denotes the module ordering (giving priority to the component): denotes the module ordering (giving priority to the component):
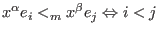 or ( or (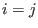 and and
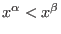 ). ).
Example:
| | ring r = 0, (x,y,z), (C,lp);
[x+y2,z3+xy];
==> xy*gen(2)+z3*gen(2)+x*gen(1)+y2*gen(1)
[x,x,x];
==> x*gen(3)+x*gen(2)+x*gen(1)
|
- (<,c):
-
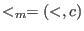 denotes the module ordering (giving priority to the coefficients): denotes the module ordering (giving priority to the coefficients):
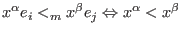 or ( or (
 and and 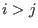 ). ).
Example:
| | ring r = 0, (x,y,z), (lp,c);
[x+y2,z3+xy];
==> xy*gen(2)+x*gen(1)+y2*gen(1)+z3*gen(2)
[x,x,x];
==> x*gen(1)+x*gen(2)+x*gen(3)
|
- (c,<):
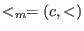 denotes the module ordering (giving priority to the component): denotes the module ordering (giving priority to the component):
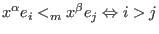 or ( or (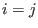 and and
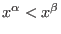 ). ).
Example:
| | ring r = 0, (x,y,z), (c,lp);
[x+y2,z3+xy];
==> [x+y2,xy+z3]
[x,x,x];
==> [x,x,x]
|
The output of a vector 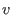 in in ![$K[x]^r$](sing_533.png) with components with components
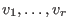 has the format has the format
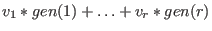 (up to permutation) unless the ordering starts with (up to permutation) unless the ordering starts with c.
In this case a vector is written as
![$[v_1, \ldots, v_r]$](sing_550.png) .In all cases SINGULAR can read input in both formats. .In all cases SINGULAR can read input in both formats.
|