|
|
C.1 Standard bases
Definition
Let
![$R = \hbox{Loc}_< K[\underline{x}]$](sing_584.png) and let and let 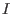 be a submodule of be a submodule of 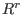 .
Note that for r=1 this means that .
Note that for r=1 this means that 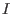 is an ideal in is an ideal in 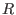 .
Denote by .
Denote by 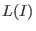 the submodule of the submodule of 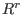 generated by the leading terms
of elements of generated by the leading terms
of elements of 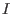 , i.e. by , i.e. by
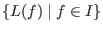 .
Then .
Then
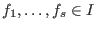 is called a standard basis of is called a standard basis of 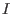 if
if
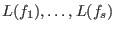 generate generate 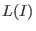 . .
A standard basis is minimal if
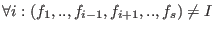 . .
A minimal standard basis is completely reduced if
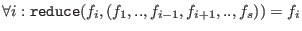
Properties
- normal form:
-
A function
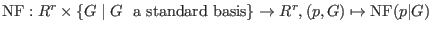 , is called a normal
form if for any , is called a normal
form if for any 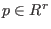 and any standard basis and any standard basis 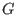 the following
holds: if the following
holds: if
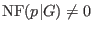 then then 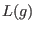 does not divide does not divide
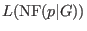 for all for all 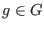 .
The function may also be applied to any generating set of an ideal:
the result is then not uniquely defined. .
The function may also be applied to any generating set of an ideal:
the result is then not uniquely defined.
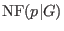 is called a normal form of is called a normal form of 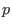 with
respect to with
respect to 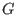 - ideal membership:
-
For a standard basis
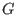 of of 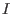 the following holds: the following holds:
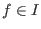 if and only if if and only if
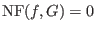 . . - Hilbert function:
- Let
![$I \subseteq K[\underline{x}]^r$](sing_598.png) be a homogeneous module, then the Hilbert function be a homogeneous module, then the Hilbert function
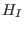 of of 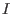 (see below)
and the Hilbert function (see below)
and the Hilbert function 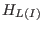 of the leading module of the leading module 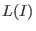 coincide, i.e.,
coincide, i.e.,
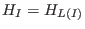 . .
|