|
|
7.3.16 nc_algebra
Syntax:
nc_algebra( matrix_expression C, matrix_expression D )
nc_algebra( number_expression n, matrix_expression D )
nc_algebra( matrix_expression C, poly_expression p )
nc_algebra( number_expression n, poly_expression p )
Type:
- ring
Purpose:
- Executed in the basering
r, say, in k variables
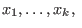 nc_algebra creates and returns the
non-commutative extension of r subject to relations
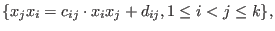 where
where 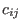 and and 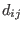 must be put into two strictly upper triangular matrices must be put into two strictly upper triangular matrices C with entries
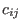 from the ground field of from the ground field of r
and D with (commutative) polynomial entries
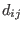 from from r. See all the details in G-algebras.
If
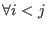 , , 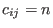 ,one can input the number ,one can input the number n instead of matrix C.
If
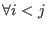 , , 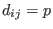 ,one can input the polynomial ,one can input the polynomial p instead of matrix D.
Note: The returned ring should be activated afterwards, using the command setring.
Remark:
- At present, PLURAL does not check the non-degeneracy conditions (see G-algebras) while setting an algebra.
Example:
| | LIB "nctools.lib";
// ------- first example: C, D are matrices --------
ring r1 = (0,Q),(x,y,z),Dp;
minpoly = rootofUnity(6);
matrix C[3][3];
matrix D[3][3];
C[1,2]=Q2; C[1,3]=1/Q2; C[2,3]=Q2;
D[1,2]=-Q*z; D[1,3]=1/Q*y; D[2,3]=-Q*x;
def S=nc_algebra(C,D);
// this algebra is a quantum deformation U'_q(so_3),
// where Q is a 6th root of unity
setring S;S;
==> // coefficients: QQ[Q]/(Q2-Q+1)
==> // number of vars : 3
==> // block 1 : ordering Dp
==> // : names x y z
==> // block 2 : ordering C
==> // noncommutative relations:
==> // yx=(Q-1)*xy+(-Q)*z
==> // zx=(-Q)*xz+(-Q+1)*y
==> // zy=(Q-1)*yz+(-Q)*x
kill r1,S;
// ----- second example: number n=1, D is a matrix
ring r2=0,(Xa,Xb,Xc,Ya,Yb,Yc,Ha,Hb),dp;
matrix d[8][8];
d[1,2]=-Xc; d[1,4]=-Ha; d[1,6]=Yb; d[1,7]=2*Xa;
d[1,8]=-Xa; d[2,5]=-Hb; d[2,6]=-Ya; d[2,7]=-Xb;
d[2,8]=2*Xb; d[3,4]=Xb; d[3,5]=-Xa; d[3,6]=-Ha-Hb;
d[3,7]=Xc; d[3,8]=Xc; d[4,5]=Yc; d[4,7]=-2*Ya;
d[4,8]=Ya; d[5,7]=Yb; d[5,8]=-2*Yb;
d[6,7]=-Yc; d[6,8]=-Yc;
def S=nc_algebra(1,d); // this algebra is U(sl_3)
setring S;S;
==> // coefficients: QQ
==> // number of vars : 8
==> // block 1 : ordering dp
==> // : names Xa Xb Xc Ya Yb Yc Ha Hb
==> // block 2 : ordering C
==> // noncommutative relations:
==> // XbXa=Xa*Xb-Xc
==> // YaXa=Xa*Ya-Ha
==> // YcXa=Xa*Yc+Yb
==> // HaXa=Xa*Ha+2*Xa
==> // HbXa=Xa*Hb-Xa
==> // YbXb=Xb*Yb-Hb
==> // YcXb=Xb*Yc-Ya
==> // HaXb=Xb*Ha-Xb
==> // HbXb=Xb*Hb+2*Xb
==> // YaXc=Xc*Ya+Xb
==> // YbXc=Xc*Yb-Xa
==> // YcXc=Xc*Yc-Ha-Hb
==> // HaXc=Xc*Ha+Xc
==> // HbXc=Xc*Hb+Xc
==> // YbYa=Ya*Yb+Yc
==> // HaYa=Ya*Ha-2*Ya
==> // HbYa=Ya*Hb+Ya
==> // HaYb=Yb*Ha+Yb
==> // HbYb=Yb*Hb-2*Yb
==> // HaYc=Yc*Ha-Yc
==> // HbYc=Yc*Hb-Yc
kill r2,S;
// ---- third example: C is a matrix, p=0 is a poly
ring r3=0,(a,b,c,d),lp;
matrix c[4][4];
c[1,2]=1; c[1,3]=3; c[1,4]=-2;
c[2,3]=-1; c[2,4]=-3; c[3,4]=1;
def S=nc_algebra(c,0); // it is a quasi--commutative algebra
setring S;S;
==> // coefficients: QQ
==> // number of vars : 4
==> // block 1 : ordering lp
==> // : names a b c d
==> // block 2 : ordering C
==> // noncommutative relations:
==> // ca=3ac
==> // da=-2ad
==> // cb=-bc
==> // db=-3bd
kill r3,S;
// -- fourth example : number n = -1, poly p = 3w
ring r4=0,(u,v,w),dp;
def S=nc_algebra(-1,3w);
setring S;S;
==> // coefficients: QQ
==> // number of vars : 3
==> // block 1 : ordering dp
==> // : names u v w
==> // block 2 : ordering C
==> // noncommutative relations:
==> // vu=-uv+3w
==> // wu=-uw+3w
==> // wv=-vw+3w
kill r4,S;
|
See also
ncalg_lib;
nctools_lib;
qmatrix_lib.
|