7.9.4 Bimodules and syzygies and lifts
Let
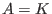
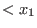 ,..., ,...,
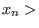 be the free algebra.
A free bimodule of rank be the free algebra.
A free bimodule of rank
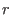 over over
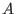 is is
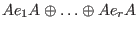 ,where ,where
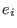 are the generators of the free bimodule. are the generators of the free bimodule.
NOTE: these
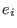 are freely non-commutative with respect to
elements of are freely non-commutative with respect to
elements of
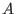 except constants from the ground field except constants from the ground field
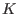 . .
The free bimodule of rank 1
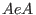 surjects onto the algebra surjects onto the algebra
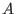 itself.
A two-sided ideal of the algebra itself.
A two-sided ideal of the algebra
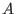 can be converted to a subbimodule of can be converted to a subbimodule of
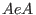 . .
The syzygy bimodule or even module of bisyzygies
of the given finitely generated subbimodule
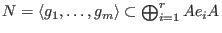 is the kernel of the natural homomorphism of is the kernel of the natural homomorphism of
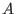 -bimodules -bimodules
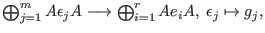 that is that is
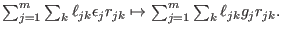
The syzygy bimodule is in general not finitely generated.
Therefore as a bimodule, both the set of generators of the
syzygy bimodule and its Groebner basis
are computed up to a specified length bound.
Given a subbimodule
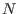 of a bimodule of a bimodule
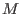 , the lift(ing) process
returns a matrix, which encodes the expression of generators , the lift(ing) process
returns a matrix, which encodes the expression of generators
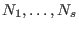
in terms of generators of
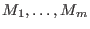 like this: like this:
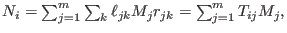
where
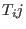 are elements from the enveloping algebra are elements from the enveloping algebra
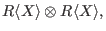 encoded as elements of the free bimodule of rank encoded as elements of the free bimodule of rank
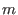 ,
namely by using the non-commutative generators of the
free bimodule which we call ,
namely by using the non-commutative generators of the
free bimodule which we call ncgen.
|