|
|
A.3.5 Handling graded modules
How to deal with graded modules in SINGULAR is best explained by
looking at an example:
| | ring R = 0, (w,x,y,z), dp;
module I = [-x,0,-z2,0,y2z], [0,-x,-yz,0,y3], [-w,0,0,yz,-z3],
[0,-w,0,y2,-yz2], [0,-1,-w,0,xz], [0,-w,0,y2,-yz2],
[x2,-y2,-wy2+xz2];
print(I);
==> -x, 0, -w, 0, 0, 0, x2,
==> 0, -x, 0, -w, -1,-w, -y2,
==> -z2,-yz,0, 0, -w,0, -wy2+xz2,
==> 0, 0, yz, y2, 0, y2, 0,
==> y2z,y3, -z3,-yz2,xz,-yz2,0
// (1) Check on degrees:
// =====================
attrib(I,"isHomog"); // attribute not set => empty output
==>
homog(I);
==> 1
attrib(I,"isHomog");
==> 2,2,1,1,0
print(betti(I,0),"betti"); // read degrees from Betti diagram
==> 0 1
==> ------------------
==> 0: 1 -
==> 1: 2 1
==> 2: 2 5
==> 3: - 1
==> ------------------
==> total: 5 7
==>
// (2) Shift degrees:
// ==================
def J=I;
intvec DV = 0,0,-1,-1,-2;
attrib(J,"isHomog",DV); // assign new weight vector
attrib(J,"isHomog");
==> 0,0,-1,-1,-2
print(betti(J,0),"betti");
==> 0 1
==> ------------------
==> -2: 1 -
==> -1: 2 1
==> 0: 2 5
==> 1: - 1
==> ------------------
==> total: 5 7
==>
intmat bettiI=betti(I,0); // degree corresponding to first non-zero row
// of Betti diagram is accessible via
// attribute "rowShift"
attrib(bettiI);
==> attr:rowShift, type int
intmat bettiJ=betti(J,0);
attrib(bettiJ);
==> attr:rowShift, type int
// (3) Graded free resolutions:
// ============================
resolution resJ = mres(J,0);
attrib(resJ);
==> attr:isHomog, type intvec
print(betti(resJ),"betti");
==> 0 1 2
==> ------------------------
==> -2: 1 - -
==> -1: 2 - -
==> 0: 1 4 -
==> 1: - - 1
==> ------------------------
==> total: 4 4 1
==>
attrib(betti(resJ));
==> attr:rowShift, type int
|
A check on degrees ((1), by using the homog command) shows that this
is a graded matrix. The homog command assigns an admissible weight
vector (here: 2,2,1,1,0) to the module I which is accessible via the
attribute "isHomog". Thus, we may think of I as a graded
submodule of the graded free
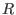 -module -module
We may also read the degrees from the Betti diagram as shown above.
The degree on the left of the first nonzero row of the Betti diagram is
accessible via the attribute "rowShift" of the betti matrix
(which is of type intmat):
(2) We may shift degrees by assigning another admissible degree vector.
Note that SINGULAR does not check whether the assigned degree
vector really is admissible. Moreover, note that all assigned
attributes are lost under a type conversion (e.g. from module to
matrix).
(3) These considerations may be applied when computing data from free resolutions (see Computation of Ext).
|
 Online Manual
Online Manual