|
|
A.3.11 Kernel of module homomorphisms
Let
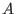 , ,
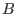 be two matrices of size be two matrices of size
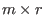 and and 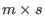 over the ring over the ring
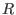 and consider the corresponding maps and consider the corresponding maps
We want to compute the kernel of the map
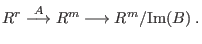 This can be done using the This can be done using the modulo command:
More precisely, the output of modulo(A,B) is a module
such that the given generating vectors span the kernel on the
right-hand side.
| | ring r=0,(x,y,z),(c,dp);
matrix A[2][2]=x,y,z,1;
matrix B[2][2]=x2,y2,z2,xz;
print(B);
==> x2,y2,
==> z2,xz
def C=modulo(A,B);
print(C); // matrix of generators for the kernel
==> yz2-x2, xyz-y2, x2z-xy, x3-y2z,
==> x2z-xz2,-x2z+y2z,xyz-yz2,0
print(A*matrix(C)); // should be in Im(B)
==> x2yz-x3,y3z-xy2, x3z+xy2z-y2z2-x2y,x4-xy2z,
==> yz3-xz2,xyz2-x2z,x2z2-yz2, x3z-y2z2
|
|