B.1 Representation of mathematical objects
SINGULAR distinguishes between objects which do not belong to a ring
and those which belong to a specific ring (see Rings and orderings).
We comment only on the latter ones.
Internally all ring-dependent objects are polynomials or structures built from
polynomials (and some additional information).
Note that SINGULAR stores (and hence prints) a polynomial automatically
w.r.t. the monomial ordering.
The definition of ideals and matrices, respectively, is straight forward:
The user gives a list of polynomials
which generate the ideal, resp. which are the entries of the matrix.
(The number of rows and columns need to be provided when creating the matrix.)
A vector in SINGULAR is always an element of a free module over the
basering. It is given as a list of polynomials in one of the following
formats
![$[f_1,...,f_n]$](sing_522.png) or or
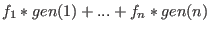 , where , where 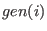 denotes the i-th canonical generator of a free module (with 1 at index i and
0 everywhere else).
Both forms are equivalent. A vector is internally represented in
the second form with the denotes the i-th canonical generator of a free module (with 1 at index i and
0 everywhere else).
Both forms are equivalent. A vector is internally represented in
the second form with the
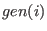 being "special" ring variables, ordered accordingly to the monomial ordering.
Therefore, the form being "special" ring variables, ordered accordingly to the monomial ordering.
Therefore, the form
![$[f_1,...,f_n]$](sing_522.png) serves as output only if the monomial ordering gives priority to the
component, i.e., is of the form serves as output only if the monomial ordering gives priority to the
component, i.e., is of the form (c,...) (see Module orderings). However, in any case the procedure show from the
library inout.lib displays the bracket format.
A vector
![$v=[f_1,...,f_n]$](sing_525.png) should always be considered as a column vector in a free module
of rank equal to
nrows( should always be considered as a column vector in a free module
of rank equal to
nrows(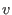 )where
nrows( )where
nrows(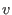 )is equal to the maximal index )is equal to the maximal index
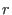 such that such that
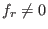 .This is due to the fact, that internally .This is due to the fact, that internally
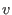 is a polynomial in a sparse representation, i.e., is a polynomial in a sparse representation, i.e.,
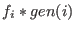 is not stored if is not stored if
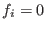 (for reasons of efficiency), hence the last 0-entries of (for reasons of efficiency), hence the last 0-entries of
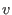 are lost.
Only more complex structures are able to keep the rank. are lost.
Only more complex structures are able to keep the rank.
A module
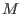 in SINGULAR is given by a list of vectors in SINGULAR is given by a list of vectors
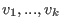 which generate the module as a submodule of the free module of rank
equal to
nrows( which generate the module as a submodule of the free module of rank
equal to
nrows(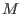 )which is the maximum of
nrows( )which is the maximum of
nrows(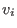 ). ).
If one wants to create a module with a larger rank than given by its
generators, one has to use the command attrib(M,"rank",r) (see
attrib, nrows) or to define a matrix first, then converting it
into a module. Modules in SINGULAR are almost the same as
matrices, they may be considered as sparse representations of matrices.
A module of a matrix is generated by the columns of the matrix and a
matrix of a module has as columns the generators of the module. These
conversions preserve the rank and the number of generators, resp. the
number of rows and columns.
By the above remarks it might appear that SINGULAR is only able to handle
submodules of a free module. However, this is not true. SINGULAR
can compute with any finitely generated module over the basering
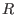 .Such a module, say .Such a module, say
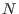 ,is not represented by its generators but by its
(generators and) relations. This means that ,is not represented by its generators but by its
(generators and) relations. This means that
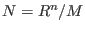 where where 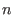 is the number of generators of is the number of generators of
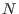 and and
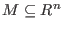 is the module of relations.
In other words, defining a module is the module of relations.
In other words, defining a module
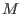 as a submodule of a free module as a submodule of a free module
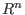 can also be considered as the definition of can also be considered as the definition of
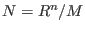 . .
Note that most functions, when applied to a module
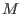 ,really deal with ,really deal with
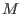 .However, there are some functions which deal with .However, there are some functions which deal with
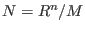 instead of instead of 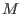 . .
For example, std(M) computes a standard basis of
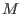 (and thus gives another representation of (and thus gives another representation of
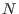 as as 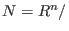 std( std(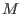 )).However, )).However, dim(M), resp. vdim(M), return
dim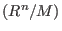 , resp. dim , resp. dim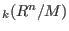 (if M is given by a standard basis). (if M is given by a standard basis).
The function syz(M) returns the first syzygy module of
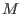 ,i.e., the module
of relations of the given generators of ,i.e., the module
of relations of the given generators of
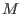 which is equal to the second syzygy module of which is equal to the second syzygy module of
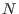 .Refer to the description of each function in
Functions to get information which module the function deals with. .Refer to the description of each function in
Functions to get information which module the function deals with.
The numbering in res and other commands for computing resolutions
refers to a resolution of
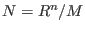 (see res; Syzygies and resolutions). (see res; Syzygies and resolutions).
It is possible to compute in any field which is a valid ground field in
SINGULAR. For doing so, one has to define a ring with the desired
ground field and at least one variable. The elements of the field are of
type number, but may also be considered as polynomials (of degree
0). Large computations should be faster if the elements of the field are
defined as numbers.
The above remarks do also apply to quotient rings. Polynomial data are
stored internally in the same manner, the only difference is that this
polynomial representation is in general not unique. reduce(f,std(0))
computes a normal form of a polynomial f in a quotient ring (cf.
reduce).
|
 Online Manual
Online Manual