|
|
D.15.7 hodge_lib
- Library:
- hodge.lib
- Purpose:
- Algorithms for Hodge ideals
- Authors:
- Guillem Blanco, email: guillem.blanco@kuleuven.be
- Overview:
- A library for computing the Hodge ideals [MP19] of Q-divisors associated to any reduced hypersurface
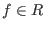 . .
The implemented algorithm [Bla21] is based on the characterization of the Hodge ideals in terms of the
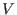 -filtration of Malgrange and Kashiwara on -filtration of Malgrange and Kashiwara on
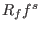 , see [MP20]. , see [MP20].
As a consequence, this library provides also an algorithm to compute the multiplier ideals and the jumping numbers of any hypersurface, see [BS05].
- References:
[Bla21] G. Blanco, An algorithm for Hodge ideals, to appear.
[BS05] N. Budur, M. Saito, Multiplier ideals, V-filtration, and spectrum, J. Algebraic Geom. 14 (2005), no. 2, 269-282. 2, 4
[MP19] M. Mustata, M. Popa: Hodge ideals, Mem. Amer. Math. Soc. 262 (2019), no. 1268
[MP20] M. Mustata, M. Popa: Hodge ideals for Q-divisors, V-filtration, and minimal exponent, Forum Math. Sigma 8 (2020), no. e19, 41 pp.
Procedures:
![]()
-generators for the
![]()
-filtration on
![]()
truncated up to degree
![]()
in
![]()
.
![]()
up to level
![]()
, for a reduced hypersurface
![]()
.
![]()
.
![]()
-th Hodge ideal
![]()
of
![]()
compute the
![]()
-th Hodge ideal assuming that the Hodge filtration of the underlying mixed Hodge module is generated at level less than or equal to
![]()
.
See also:
dmodapp_lib.
|









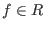 .
.
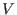 -filtration of Malgrange and Kashiwara on
-filtration of Malgrange and Kashiwara on
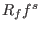 , see [MP20].
, see [MP20].