|
|
D.15.7.4 nextHodgeIdeal
Procedure from library hodge.lib (see hodge_lib).
- Usage:
- nextHodgeIdeal(f, I, p); f a poly, I an ideal, p a non-negative integer
- Return:
- ideal
- Purpose:
- given the
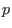 -th Hodge ideal -th Hodge ideal
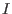 of of
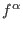 compute the compute the
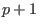 -th Hodge ideal assuming that -th Hodge ideal assuming that
the Hodge filtration of the underlying mixed Hodge module is generated at level less than or equal to
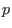 . .
Example:
| | LIB "hodge.lib";
ring R = 0,(x,y),dp;
poly f = y^2-x^3;
def Ra = hodgeIdeals(f, 2);
setring(Ra);
int p = 1;
nextHodgeIdeal(y^2-x^3, hodge[3][1][p+1], p);
==> _[1]=x^2*y^2
==> _[2]=y^3
==> _[3]=x^3*y
==> _[4]=x^4+(2*a+1)*x*y^2
|
|





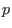 -th Hodge ideal
-th Hodge ideal
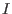 of
of
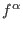 compute the
compute the
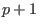 -th Hodge ideal assuming that
-th Hodge ideal assuming that
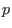 .
.