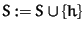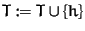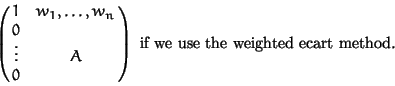


Next: 3. Examples and comparisons
Up: Standard bases, syzygies and
Previous: 1. A standard basis
In SINGULAR the standard basis algorithm is implemented as follows:
-
- S := StandardBasis
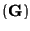
INPUT: G, a set of polynomial vectors
![$\subset K[x]^r$](img196.gif)
OUTPUT: S, a standard base of the submodule generated by G with
respect to the given monomial ordering
-
- S := Gh
update (S)
HCtest
T := S
L := initPairs (S)
clear (S)
WHILE
 DO
DO
-
-
p := (a, b, s) the last element from L
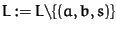
IF the spoly of a and b is not computed yet THEN
-
- s := spoly (a, b)
END
h := LazyNF (p | T)
IF
 THEN
THEN
-
- HCtest
updatePairs (h)
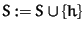
clear (S)
END
END
S:= completeReduce (S).
Remark 2..1
In cases when either < is a wellordering, or
![$G \subseteq K[x]$](img111.gif)
and
![$\dim_K K[x]/ \langle G \rangle < \infty$](img199.gif)
the standard basis is uniquely determined. Moreover, in this case we can achieve a
presentation
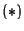
as in
1.12 (2) with
![$\xi_i \in K[x]$](img191.gif)
,
![$h \in
K[x]^r$](img176.gif)
.
During the algorithm the set S is sorted by increasing monomial ordering of
the leading terms of the elements with respect to
The set T (respectively L) is sorted by increasing (respectively
decreasing) monomial ordering of the leading terms of the elements
(respectively the S-polynomial of the corresponding pair) with respect to
or
Now we explain the procedures used in the standard basis algorithm:
Update 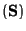
INPUT: S, a set of polynomial vectors
OUTPUT: S, the set of polynomial vectors after the interreduction
for all 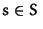 DO
DO 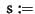 NFBuchberger
NFBuchberger
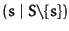 .
.
HCtest
INPUT: S, a set of polynomials
OUTPUT: a boolean value (does a ``highest corner'' exist?)
and, if so, the monomial ``highest corner''
If
![$G \subseteq K[x]$](img111.gif) (that is r = 1) then it tests if there are
(that is r = 1) then it tests if there are
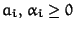 such that
such that
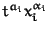 occur as leading terms in S for all i. If this is true it computes the minimal
monomial
occur as leading terms in S for all i. If this is true it computes the minimal
monomial 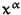 (with respect to the ordering < in K[x]) which is not
in the ideal generated by the leading terms of the elements of S(t = 1).
This monomial is called ``highest corner''.
(with respect to the ordering < in K[x]) which is not
in the ideal generated by the leading terms of the elements of S(t = 1).
This monomial is called ``highest corner''.
It changes the polynomial arithmetic to cancel all monomials
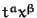 with
with
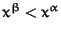 in further computations.
in further computations.
Remark 2..2
Notice that the highest corner
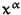
is equal to 1 in the case of a wellordering.
Therefore, the procedure is called only if
xi < 1 for some
i. The
highest corner is computed in a combinatorial manner.
1cm
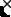
 correspond to leading terms of S(t = 1),
correspond to leading terms of S(t = 1), 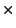 corresponds to the ``highest corner''
corresponds to the ``highest corner'' 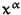 .
.
 initPairs
initPairs 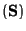
INPUT: S, a set of (interreduced) polynomial vectors
OUTPUT: L, the set of critical pairs
It creates the pairset
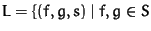 , s the leading term
of spoly
, s the leading term
of spoly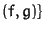 . Using the criteria similar to Gebauer-Möller (cf. [GM]) useless pairs are cancelled.
. Using the criteria similar to Gebauer-Möller (cf. [GM]) useless pairs are cancelled.
We have two options: usually the criteria are applied for the
pairs
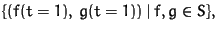 that is in K[x]. In the
option sugar crit we apply it to L using the idea of [GMNRT].
that is in K[x]. In the
option sugar crit we apply it to L using the idea of [GMNRT].
Clear 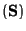
INPUT and OUTPUT: S, a set of polynomial vectors
Deletes f from S if
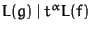 for some
for some 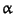 and
and 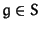 .
.
Update 
INPUT and OUTPUT: h, a polynomial vector
-
- IF sugar THEN RETURN END
IF t|h THEN
-
- choose
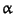 maximal such that
maximal such that
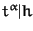
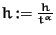
END
UpdatePairs 
INPUT: h, a polynomial vector
S, a set of polynomial vectors
OUTPUT: L, the set of critical pairs from S and h
-
- It updates the pairset L.
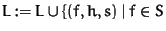 ,
s the leading term of spoly
,
s the leading term of spoly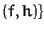 .
.
The criteria to cancel useless pairs are used as in initPairs.
h := LazyNF
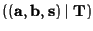
INPUT: s, a polynomial vector to reduce
(a,b), the critical pair from which s is
the spoly
T, a set of polynomials with which to
reduce
OUTPUT: h, the reduced polynomial vector
-
- h := s
WHILE exist 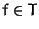 such that
such that
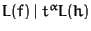 for some
for some 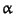 DO
DO
-
- choose the first possible f with respect to the ordering in T
such that
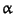 is minimal.
is minimal.
IF
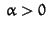 THEN
THEN
-
- IF the position of (a, b, h) in L is not the last one
THEN
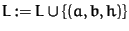
RETURN 0
END
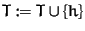
NFupdate pairs (h)
END
h:= spoly
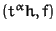
update (h)
IF degree (h) > degree(s) and
the position of (a, b, h) in L is not the last one THEN
-
-
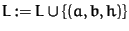
RETURN 0
END
END
NFupdatePairs 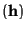
INPUT: h, a polynomial vector
S, a set of polynomial vectors
OUTPUT: L the set of some critical pairs from S and h
-
- IF NOT more pairs THEN RETURN END
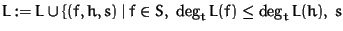 the
leading term of spoly
the
leading term of spoly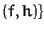
The criteria to cancel useless pairs are used as in initPairs.
Remark 2..3
The option
morePairs (=
more pairs in NFupdatePairs) has the effect of keeping some useless pairs
in order to have better candidates for reduction. The leading idea is to
keep (some of) those pairs which could not be discarded if we had used
Lazard's method. In the case of a non-wellordering this has turned out to
be useful, since it can help in not creating polynomials with too long tails
during the normal form computation.
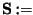 completeReduce
completeReduce 
INPUT and OUTPUT: S, a set of polynomial vectors
-
- IF < is a wellordering or
![$(S \subseteq K[x]$](img232.gif) and
and
![$\dim_K K[x]/
\langle S \rangle < \infty)$](img233.gif)
THEN
-
-
S:= S(t=1)
FOR all 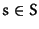 DO
DO
-
- s := redtail (s|S)
END
ELSE
-
- FOR all
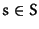 DO
DO
-
- s := redtail (s|S)
END
S := S(t = 1)
END
 redtail
redtail 
INPUT and OUTPUT: s, a polynomial vector
reduces the monomial below L(s) with elements from S as long as possible.



Next: 3. Examples and comparisons
Up: Standard bases, syzygies and
Previous: 1. A standard basis
| ZCA Home |
Reports |
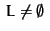 DO
DO
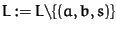
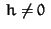 THEN
THEN