- 1)
-
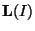 denotes the ideal of
denotes the ideal of
![$K[\underline{x}]$](img43.gif) generated by
generated by
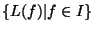 .
.
- 2)
-
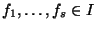 is called a standard basis of I if
is called a standard basis of I if
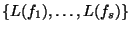 generates the ideal
generates the ideal
![$L(I) \subset K[\underline{x}]$](img62.gif) .
.
SINGULAR example: A standard basis computation:
// define a ring R= (Z/32003)[x,y,z]
ring R = 32003, (x,y,z), dp ;
// define 3 polynomials
poly s1 = x^3*y^2 + 151*x^5*y + 169*x^2*y4
+ 151*x^2*y*z3 + 186*x*y^6 + 169*y^9;
poly s2 = x^2*y^2*z^2 + 3*z^8;
poly s3 = 5*x^4*y^2 + 4*x*y^5 + 2x^2*y^2*z^3 + y^7 + 11*x^10;
// define the ideal i generated by s1,s2,s3
ideal i = s1, s2, s3;
// compute standard basis j of i
ideal j = std(i);
// display j;
j;