


Next: 2 Heuristic simplification of
Up: 4 CR simplification strategies
Previous: 4 CR simplification strategies
1 Heuristic simplification of polynomial CR expressions
Given CR a expression 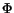 ,
we first isolate all polynomial CR
sub-expressions of
,
we first isolate all polynomial CR
sub-expressions of 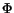 and consider the simplification of each
polynomial CR sub-expression independently. Since a CR simplification
follows the CR construction, we may assume that the
expressions considered are polynomial CR expressions whose leaves are
simple, one - dimensional CRs.
and consider the simplification of each
polynomial CR sub-expression independently. Since a CR simplification
follows the CR construction, we may assume that the
expressions considered are polynomial CR expressions whose leaves are
simple, one - dimensional CRs.
Secondly, we determine the dimension of the polynomial CR expression and
handle the simplification of one- and multi - dimensional CR expressions
separately.
For both cases, the suggested simplification heuristic makes use of
the degree of a polynomial CR expression, which is defined as
follows:
Based on this definition, we suggest a simplification algorithm for the
one - dimensional case which is based on the observation that a
one - dimensional polynomial CR expression 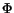 can
be transformed into a polynomial CR of length
can
be transformed into a polynomial CR of length
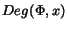 .
.
Algorithm CRPOLYSIMP1D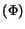
-
- Input:
- Polynomial CR expression
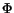 with
with
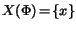
- Output:
- Simplified polynomial CR expression
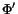 with
with
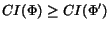
- (A)
- If
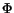 is a constant or a CR then return
is a constant or a CR then return 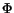 ;
;
- (B)
- If
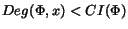 then
then
- 1.
- Recursively simplify
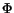 by
unconditionally applying the simplification rules
(1) - (6) and return the resulting
polynomial CR of length cs;
by
unconditionally applying the simplification rules
(1) - (6) and return the resulting
polynomial CR of length cs;
- (C)
- else if
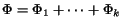 then
then
- 1.
- Set
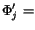 CRPOLYSIMP1D
CRPOLYSIMP1D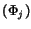 for
for
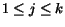 ;
;
- 2.
- Transform all constant or polynomial CRs among the returned
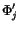 into one polynomial CR (or constant) by applying
the rules (1) and (3) and return
the resulting CR expression.
into one polynomial CR (or constant) by applying
the rules (1) and (3) and return
the resulting CR expression.
- (D)
- else if
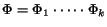 then
then
- 1.
- Set
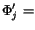 CRPOLYSIMP1D
CRPOLYSIMP1D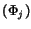 for
for
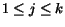 ;
;
- 2.
- Transform all constant or polynomial CRs among the returned
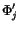 into one constant or polynomial CR by applying
the rules (6) and (4) and return
the resulting CR expression.
into one constant or polynomial CR by applying
the rules (6) and (4) and return
the resulting CR expression.
- (E)
- else
 /* Now
/* Now
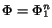 */
*/
- Set
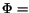 CRPOLYSIMP1D
CRPOLYSIMP1D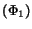 and return
and return 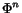
Notice that (B) is the crucial step of this algorithm, since it
determines whether or not the CR expression is fully expanded into a
polynomial CR. This is also the only step where we might lose the
optimality of the CR simplification. For example, if we consider the
CR expression
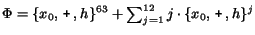 and assume that
W(<tex2htmlverbmark>26<tex2htmlverbmark>) = 1 then
and assume that
W(<tex2htmlverbmark>26<tex2htmlverbmark>) = 1 then
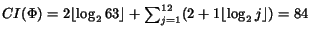 ,
,
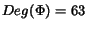 ,
and hence,
,
and hence, 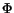 is simplified into
a polynomial CR of length 63, i.e.,
is simplified into
a polynomial CR of length 63, i.e.,
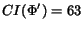 .
However,
a simplification into
.
However,
a simplification into
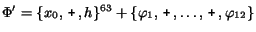 would yield
would yield
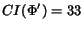 ,
which is better.
However, such cases could only be remedied by backtracking
algorithms which, by their very nature, have a (worst-case) exponential
time complexity.
,
which is better.
However, such cases could only be remedied by backtracking
algorithms which, by their very nature, have a (worst-case) exponential
time complexity.
The heuristic simplification of n-dimensional polynomial CR
expressions is similar to the one - dimensional case. However, in
addition to determining whether or not to expand the expression
into a polynomial CR, we also have to determine a variable ordering
for the expansion. Furthermore, we have to take the complexity of the
evaluation grid into consideration, since the CI of multi - dimensional
CR expressions depends on the number of evaluation points for each
variable.
Algorithm CRPOLYSIMPND
-
- Input:
- Polynomial CR expression
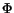 with
with
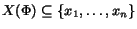 ,
,
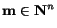
- Output:
- Simplified polynomial CR expression
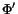 with
with
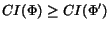
- (A)
- If
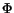 is a constant or a CR then return
is a constant or a CR then return 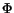 ;
;
- (B)
- If
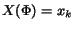 then return CRPOLYSIMP1D
then return CRPOLYSIMP1D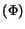 ;
;
- (C)
- Let
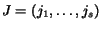 be a tuple of
s integers, such that
be a tuple of
s integers, such that
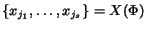 and for all
and for all
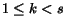 :
djk < dj<<547>>k+1 or
djk = dj<<549>>k+1 and
:
djk < dj<<547>>k+1 or
djk = dj<<549>>k+1 and
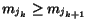 ,
where
,
where
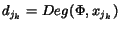 ;
;
- (D)
- If
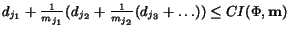 then
then
- 1.
- Recursively simplify
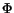 by
unconditionally applying the simplification rules
(1) - (6) with the variable
ordering
by
unconditionally applying the simplification rules
(1) - (6) with the variable
ordering
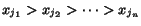 and return the
result.
and return the
result.
- (C)
- else if
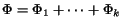 then
then
- 1.
- Set
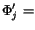 CRPOLYSIMPND
CRPOLYSIMPND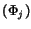 for
for
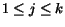 ;
;
- 2.
- Merge constant or polynomial CRs among the returned
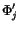 as much as possible by applying
the rules (1) and (3) and return
the resulting CR expression.
as much as possible by applying
the rules (1) and (3) and return
the resulting CR expression.
- (D)
- else if
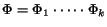 then
then
- 1.
- Set
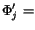 CRPOLYSIMPND
CRPOLYSIMPND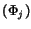 for
for
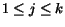 ;
;
- 2.
- Merge constants or one - dimensional polynomial CRs among the returned
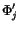 as much as possible by applying
the rules (6) and (4) and return
the resulting CR expression.
as much as possible by applying
the rules (6) and (4) and return
the resulting CR expression.
- (E)
- else
 /* Now
/* Now
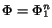 */
*/
- Set
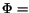 CRPOLYSIMPND
CRPOLYSIMPND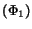 and return
and return 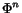
Notice that the variable ordering is determined in step (C). Our
heuristic for determining this ordering is based on the observation
that for any variable ordering
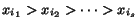 ,
,
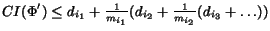 .
Hence, by choosing the variable
ordering
.
Hence, by choosing the variable
ordering
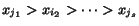 as done in step (C),
we minimize the upper bound for the CI of the respective fully
expanded polynomial CR.
as done in step (C),
we minimize the upper bound for the CI of the respective fully
expanded polynomial CR.
Various small and tedious to describe, but more or less obvious
improvements to the algorithm above should be added. For example, in
step C.1 (resp. D.1), we should collect all
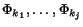 for which
for which
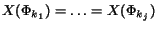 and
call the algorithm recursively with the expressions
and
call the algorithm recursively with the expressions
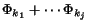 as arguments (provided they are different from
as arguments (provided they are different from
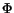 )
instead of calling the algorithm recursively with each single
)
instead of calling the algorithm recursively with each single
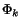 as argument. This way, we enable a finer grained
simplification of CR expressions which contains the same variables.
as argument. This way, we enable a finer grained
simplification of CR expressions which contains the same variables.
Let us look at some examples by considering the simplification of
two-dimensional polynomial CR expressions over the variables x and
y: To simplify our notation, let us write x for the CR
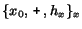 ,
y for the CR
,
y for the CR
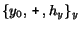 ,
and
xl (resp. yl) for a CR of the form
,
and
xl (resp. yl) for a CR of the form
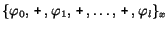 for some constants
for some constants
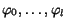 .
Furthermore, let us suppose that
.
Furthermore, let us suppose that
 and that
W(<tex2htmlverbmark>27<tex2htmlverbmark>) = 1. Then each entry in table
2 shows a two-dimensional CR expression with its
CI. Column 1 shows the unsimplified CR expression, column 2 and 3
show the fully-expanded polynomial CRs with the variable ordering
x>y and y>x, respectively. Column 4 shows the CR expression returned by the
algorithm CRPOLYSIMPND and column 5 shows the respective CR
expression with the minimal CI.
and that
W(<tex2htmlverbmark>27<tex2htmlverbmark>) = 1. Then each entry in table
2 shows a two-dimensional CR expression with its
CI. Column 1 shows the unsimplified CR expression, column 2 and 3
show the fully-expanded polynomial CRs with the variable ordering
x>y and y>x, respectively. Column 4 shows the CR expression returned by the
algorithm CRPOLYSIMPND and column 5 shows the respective CR
expression with the minimal CI.
Table 2:
Examples for simplifications of two-dimensional polynomial CR expressions
 |
Obviously, the larger the degree of the CR expressions, the
larger the difference between the various simplification methods.
However, the examples in table 2 already illustrate
that a simplification algorithm which would fully expand a given CR
expression (using any variable ordering) is inferior to CRPOLYSIMPND, and that CRPOLYSIMPND is not as good as the
exhaustive search simplification algorithm.



Next: 2 Heuristic simplification of
Up: 4 CR simplification strategies
Previous: 4 CR simplification strategies
| ZCA Home |
Reports |
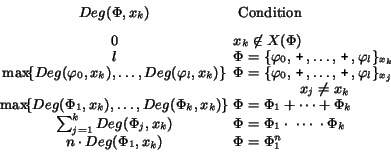
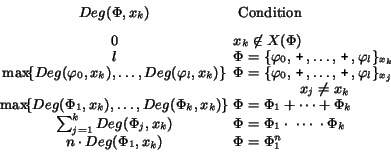
![]() can
be transformed into a polynomial CR of length
can
be transformed into a polynomial CR of length
![]() .
.
![]()
![]()
![]() for which
for which
![]() and
call the algorithm recursively with the expressions
and
call the algorithm recursively with the expressions
![]() as arguments (provided they are different from
as arguments (provided they are different from
![]() )
instead of calling the algorithm recursively with each single
)
instead of calling the algorithm recursively with each single
![]() as argument. This way, we enable a finer grained
simplification of CR expressions which contains the same variables.
as argument. This way, we enable a finer grained
simplification of CR expressions which contains the same variables.
![]() ,
y for the CR
,
y for the CR
![]() ,
and
xl (resp. yl) for a CR of the form
,
and
xl (resp. yl) for a CR of the form
![]() for some constants
for some constants
![]() .
Furthermore, let us suppose that
.
Furthermore, let us suppose that
![]() and that
W(<tex2htmlverbmark>27<tex2htmlverbmark>) = 1. Then each entry in table
2 shows a two-dimensional CR expression with its
CI. Column 1 shows the unsimplified CR expression, column 2 and 3
show the fully-expanded polynomial CRs with the variable ordering
x>y and y>x, respectively. Column 4 shows the CR expression returned by the
algorithm CRPOLYSIMPND and column 5 shows the respective CR
expression with the minimal CI.
and that
W(<tex2htmlverbmark>27<tex2htmlverbmark>) = 1. Then each entry in table
2 shows a two-dimensional CR expression with its
CI. Column 1 shows the unsimplified CR expression, column 2 and 3
show the fully-expanded polynomial CRs with the variable ordering
x>y and y>x, respectively. Column 4 shows the CR expression returned by the
algorithm CRPOLYSIMPND and column 5 shows the respective CR
expression with the minimal CI.