- ... bases1
- Note
that similar concepts appear in a paper of Hironaka where the notion of a complete set of polynomials is called a standard basis [Hi64].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... admissible2
- A term
ordering
 is called admissible if for every term s,t,u,
is called admissible if for every term s,t,u,
 holds, and
holds, and
 implies
implies
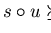 .
An ordering fulfilling the latter condition is also said to be
compatible with the respective multiplication
.
An ordering fulfilling the latter condition is also said to be
compatible with the respective multiplication  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ring3
 denotes the rational numbers.
denotes the rational numbers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
zero4
- Note that we always assume that the reduction in the ring is effective.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... multiplication5
- When studying monoid rings over reduction rings it is possible
that the ordering on the ring is not compatible with scalar multiplication
as well as with multiplication with monomials or polynomials.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... effective6
- By ``effective'' we mean that
given an element we can decide whether a successor exists and then
construct it.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
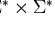 7
7
 is the
set of all words on the
alphabet
is the
set of all words on the
alphabet  where
where  presents the empty word, i.e.,
the word of length zero, and
presents the empty word, i.e.,
the word of length zero, and  the identity on words.
the identity on words.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... admissible8
- An ordering on
 is called
admissible, if for all
is called
admissible, if for all
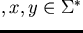 ,
,
 holds
and
holds
and  implies
implies
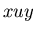 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... polynomials9
- Note that we use
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... divisibility10
- We call a term t (right) divisible by a term x in case there exists a term z such that
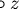 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... polynomials11
- Notice
that p1=p2 is possible.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... shows12
- This property is important
for introducing interreduction to a completion procedure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... non-constant13
- A
constant polynomial is an element in
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... none14
-
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
- By theorem
2.2 the existence of such finite bases would solve the
subgroup problem for groups presented by convergent
semi-Thue systems.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
 holds, and
holds, and
 implies
implies
 implies
implies