


Next: 4. Group Rings
Up: String Rewriting and Gröbner
Previous: 2. Fundamental Relations Between
3. Defining Reduction in
![${\bf K}[{\cal M}]$](img1.gif)
Throughout this paper let  be a monoid presented by a finite
convergent semi-Thue system
be a monoid presented by a finite
convergent semi-Thue system
 and
and  the
well-founded ordering
on
the
well-founded ordering
on  induced by the completion ordering of its presentation.
Notice that although the completion ordering is compatible on
induced by the completion ordering of its presentation.
Notice that although the completion ordering is compatible on
 with concatenation, this in general no longer holds for the
ordering
with concatenation, this in general no longer holds for the
ordering  on
on  with respect to the multiplication
with respect to the multiplication  on
on
 .
For example groups do not allow compatible well-founded orderings due
to the existence of inverse elements.
Given a non-zero polynomial p in
.
For example groups do not allow compatible well-founded orderings due
to the existence of inverse elements.
Given a non-zero polynomial p in
![${\bf K}[{\cal M}]$](img1.gif) ,
the head term
,
the head term
 is the
largest term in p with respect to
is the
largest term in p with respect to  ,
,
 is the
coefficient of this term and
is the
coefficient of this term and
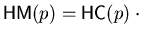 the
head monomial.
the
head monomial.
 is the set of terms occurring in
p.
The ordering on
is the set of terms occurring in
p.
The ordering on  can be extended to a partial ordering on
can be extended to a partial ordering on
![${\bf K}[{\cal M}]$](img1.gif) by setting p > q if and only if
by setting p > q if and only if
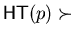 or
or
 and
and
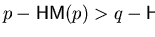 ,
and this ordering is Noetherian.
Frequently in polynomial rings reduction is defined by
using the head monomial of a polynomial as a left hand side of a
rule in case the head term of the
polynomial is a divisor of the term of the monomial to be reduced.
But defining reduction in this way for monoid rings need not be
Noetherian as the following example shows.
,
and this ordering is Noetherian.
Frequently in polynomial rings reduction is defined by
using the head monomial of a polynomial as a left hand side of a
rule in case the head term of the
polynomial is a divisor of the term of the monomial to be reduced.
But defining reduction in this way for monoid rings need not be
Noetherian as the following example shows.
Example 3..1
Let
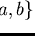
and
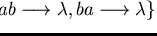
be a presentation of a group

with a
length-lexicographical ordering induced by

.
Suppose we simply require divisibility
10 of the head term to allow reduction.
Then we could reduce the
polynomial
![$b^2 + 1 \in {\bf Q}[{\cal G}]$](img186.gif)
at the monomial
b2 by the polynomial
a +
b as
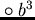
.
This would give us:
and the polynomial
-
b4 + 1 likewise would be reducible by
a +
b at the monomial -
b4 causing an
infinite reduction sequence.
Hence we will need additional restrictions in order to prevent
that a monomial is replaced by a larger polynomial.
Since our monoid  in general is not commutative, we will restrict ourselves
to right ideals - hence to right multiples - and inspect two variations of defining right reduction.
For further variants see e.g. [MaRe95,Re95].
in general is not commutative, we will restrict ourselves
to right ideals - hence to right multiples - and inspect two variations of defining right reduction.
For further variants see e.g. [MaRe95,Re95].
Definition 3..2
Let
p,
f be two non-zero polynomials in
![${\bf K}[{\cal M}]$](img1.gif)
.
We say
f strongly right reduces p to
q at
a monomial

of
p in one step, denoted by
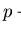
,
if
- (a)
-
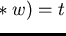 for some
for some
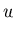 ,
and
,
and
- (b)
-
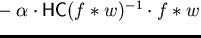 .
.
We write
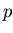
if there is a polynomial
q as defined
above and
p is then called strongly right reducible by
f.
Strong right reduction by a set
![$F \subseteq {\bf K}[{\cal M}]$](img195.gif)
is denoted by
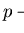
and abbreviates
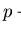
for some

.
Note that in order to strongly right reduce p, the polynomial f
need not be smaller than p.
The condition
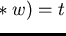 prevents reduction with a polynomial in case
prevents reduction with a polynomial in case
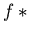 ,
i.e., if
the monomials of f eliminate each other by multiplying f with w.
This might happen in case the monoid ring contains zero-divisors.
Further, in case we have
,
i.e., if
the monomials of f eliminate each other by multiplying f with w.
This might happen in case the monoid ring contains zero-divisors.
Further, in case we have
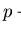 at the monomial
at the monomial
 ,
then
,
then
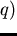 .
In order to decide, whether a polynomial f strongly right reduces a
polynomial p at a monomial
.
In order to decide, whether a polynomial f strongly right reduces a
polynomial p at a monomial
 one has to decide whether
there exist elements
one has to decide whether
there exist elements
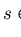 and
and
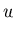 such that
such that
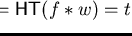 .
Since this problem is connected to solving equations
.
Since this problem is connected to solving equations
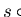 in one variable
in one variable  in the monoid
in the monoid  presented by
presented by
 ,
this problem is undecidable in general, even if
,
this problem is undecidable in general, even if  is presented by a convergent semi-Thue system.
Note that there can be no, one or even (infinitely) many solutions
depending on
is presented by a convergent semi-Thue system.
Note that there can be no, one or even (infinitely) many solutions
depending on  .
In case
.
In case  is a group the equation only has one unique solution.
is a group the equation only has one unique solution.
Example 3..3
Let
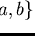
and
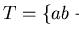
be a
presentation of a monoid

with a length-lexicographical ordering
induced by

.
Then the equation
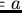
has no solution in

,
the equation
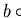
has one solution in

,
namely

,
and
the equation
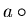
has infinitely many solutions in

,
namely the set
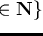
.
The following example illustrates how different monomials
can become equal when modifying a polynomial in order to use it for
strong right reduction.
Remark 3..4
Let
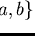
and
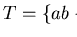
be a
presentation of a monoid

with a length-lexicographical ordering
induced by

.
Furthermore, let
f1,
f2,
p be polynomials in
![${\bf Q}[{\cal M}]$](img211.gif)
such that
f1 =
a2 +
a,
f2 =
a2
-
a and
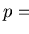
.
Then
p is strongly right reducible by
f1 at
b, as

and
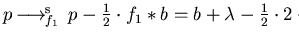
.
On the other hand, although both equations
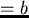
and
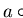
have
b as a solution, we get
that
p is not strongly right reducible by
f2, as
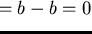
.
In case  is a right cancellative monoid or a group, the phenomenon
described in this remark can no longer occur, since
then
is a right cancellative monoid or a group, the phenomenon
described in this remark can no longer occur, since
then
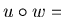 implies u = v for all
implies u = v for all
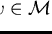 .
Let us continue to state some of the properties strong right
reduction satisfies.
.
Let us continue to state some of the properties strong right
reduction satisfies.
Unfortunately, for strong right reduction
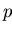 ,
,
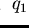 in general does not imply
in general does not imply
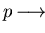 ,
as the following example shows12.
Therefore, our structure satisfies (A1), (A2) and (A3) but not (A4) of the axioms given in the introduction.
,
as the following example shows12.
Therefore, our structure satisfies (A1), (A2) and (A3) but not (A4) of the axioms given in the introduction.
Example 3..6
Let
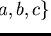
and
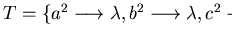
be a
monoid presentation of a group

with a length-lexicographical ordering induced
by
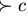
.
Looking at
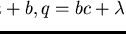
and
![$w = ac + b \in {\bf Q}[{\cal G}]$](img234.gif)
we get
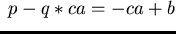
and
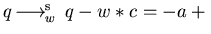
,
but
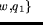
.
Trying to reduce
ba by
w or
q1 we get
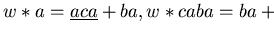
and
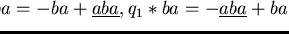
all violating condition (a) of definition
3.2.
Trying to reduce
b we get the same problem with
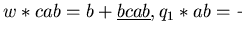
and
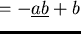
.
Nevertheless, strong right reduction has the essential properties
which allow us to characterize a right ideal by reduction with respect to
a set of generators, e.g. the translation lemma holds and the right
ideal congruence can be described by reduction.
In analogy to Buchberger we will call bases of right ideals which induce
a confluent strong right reduction describing the right ideal congruence strong Gröbner bases.
Definition 3..8
A set
![$G \subseteq {\bf K}[{\cal M}]$](img250.gif)
is called a
Gröbner basis
with respect to
the reduction

or a
strong Gröbner
basis of
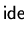
,
if

,
and

is confluent.
Notice that by lemma 3.7 we have
Lemma 3..9
For a set of polynomials
G in
![${\bf K}[{\cal M}]$](img1.gif)
,
G is a strong
Gröbner basis of
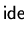
if and only if for all
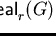
we have
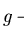
.
Unlike in Buchberger's case a polynomial itself need not be a Gröbner
basis of the right ideal it generates.
Example 3..10
Let
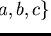
and

be a monoid presentation of a
group

with with a length-lexicographical ordering
induced by
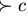
.
Further, let us consider the polynomial
![$p = a + b + c \in {\bf Q}[{\cal G}]$](img258.gif)
.
Then

is not confluent on
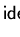
,
as we can
strongly right reduce
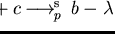
using
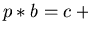
and
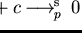
,
but although
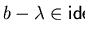
,
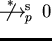
,
as for all

,
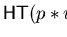
.
In accordance with the terminology used in Buchberger's approach
to give a confluence test for sets of polynomials,
we define critical pairs of polynomials
with respect to strong right reduction as situations were both polynomials
can be applied for strong reduction.
Definition 3..11
Given two non-zero polynomials
11
![$p_{1}, p_{2} \in {\bf K}[{\cal M}]$](img267.gif)
,
every pair of elements
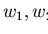
such that

,
defines a
strong s-polynomial
Let
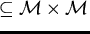
be the set containing
all such pairs
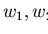
.
A strong s-polynomial will be called non-trivial in case it is non-zero and
notice that we always have
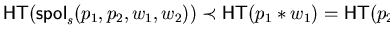 .
.
Example 3..12
Reviewing example
3.10 we find that a polynomial
can have a non-trivial strong s-polynomial with itself.
In fact since

we get
that
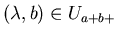
gives rise to a strong
s-polynomial
This phenomenon, which differs from the one for free monoid rings,
is due to the fact that the definition of critical
situations no longer only involves the head terms of the respective
polynomials but the whole polynomials.
The set
Up1,p2 is contained in the set of all solutions in  to the
equations in two variables of the form
to the
equations in two variables of the form
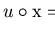 where
where
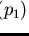 and
and
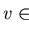 .
It can be empty, finite or even infinite.
We can now give a criterion that implies confluence
for strong right reduction in terms of strong s-polynomials.
.
It can be empty, finite or even infinite.
We can now give a criterion that implies confluence
for strong right reduction in terms of strong s-polynomials.
Notice that this theorem, although characterizing a strong Gröbner basis by
strong s-polynomials, in general does not give a finite test to check
whether a set is a strong Gröbner basis, since in general infinitely
many strong s-polynomials have to be considered.
Later on we will see that the right ideal generated by a+b+c in
example 3.10 has finite strong Gröbner bases and we
will show how to compute such a basis.
The following example shows how already
two polynomials can cause infinitely many critical situations.
Example 3..14
Let
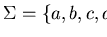
and

be a presentation of a
monoid

with a length-lexicographical ordering
induced by
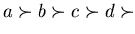
.
Further consider two polynomials
![$p_1 = a + f, p_2 = bf + a \in {\bf Q}[{\cal M}]$](img287.gif)
.
Then we get infinitely many critical situations
where
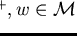
,
giving rise to infinitely many strong s-polynomials
and
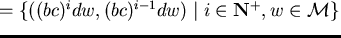
.
Notice that in contrary to the definition of s-polynomials in commutative
polynomial rings in this example there are infinitely many strong
s-polynomials originating from p1 and p2 which cannot be expressed
by monomial multiples of one or even a finite set of these s-polynomials.
Therefore, localization of critical situations in general is very hard.
As example 3.14 shows,
the set
Up1,p2 need not have a ``suitable finite basis'',
e.g. there need not exist a finite set
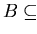 such that
for every pair
such that
for every pair
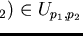 there exists a pair
there exists a pair
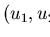 and an element
and an element
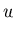 with
with
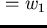 and
and
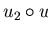 .
The subset
.
The subset
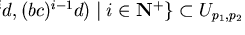 is such a basis, but it is not finite and there is in fact no finite one.
is such a basis, but it is not finite and there is in fact no finite one.
It turns out that the following uniform problem is undecidable,
even in monoids where the solvability of
equations of the form
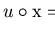 is decidable.
is decidable.
Given: Two polynomials
![$p,q \in {\bf K}[{\cal M}]$](img298.gif) ,
and
,
and
 a convergent semi-Thue system presenting
a convergent semi-Thue system presenting  .
Question: Does there exist a strong s-polynomial for p and q?
.
Question: Does there exist a strong s-polynomial for p and q?
One way to reduce the set of critical situations that have to be
considered to ensure confluence is to weaken the reduction relation
while preserving the generated equivalence relation.
The key idea is that for two reduction relations
 and
and
 on a set
on a set  such that
such that
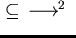 and
and
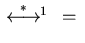 ,
the confluence of
,
the confluence of
 on
on  implies the
confluence of
implies the
confluence of
 on
on  .
.
One natural weakening strong right reduction we studied
is called right reduction.
Instead of using all right multiples of a polynomial by monomials as rules we
restrict ourselves to those right
multiples of a polynomial which allow the head
term of the polynomial to keep its head position.
Hence, reduction defined in this way can be called ``stable'' and
resembles Buchberger's definition of reduction.
The results can be found in [MaRe93b,Re95].
In the following we will introduce a further weakening of
strong reduction using prefixes in  .
Notice that such prefixes are divisors with respect to word concatenation
and hence easy to determine.
.
Notice that such prefixes are divisors with respect to word concatenation
and hence easy to determine.
Definition 3..15
Let
p,
f be two non-zero polynomials in
![${\bf K}[{\cal M}]$](img1.gif)
.
We say
f prefix reduces
p to
q at a monomial

of
p in one step, denoted by
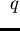
,
if
- (a)
-
 for some
for some
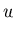 ,
i.e.,
,
i.e.,
 is a prefix of t, and
is a prefix of t, and
- (b)
-
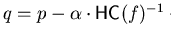 .
.
We write
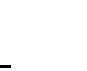
if there is a polynomial
q as defined
above and
p is then called prefix reducible by
f.
Prefix reduction by a set
![$F \subseteq {\bf K}[{\cal M}]$](img195.gif)
is denoted by
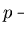
and abbreviates
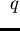
for some

.
Notice that in the above definition the equation in
(a) has at most one solution and
we then always have
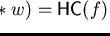 .
This is due to the fact that
.
This is due to the fact that
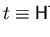 implies
implies
 and
and
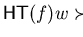 for all
for all
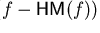 .
Further, in case f prefix reduces p to q at the monomial
.
Further, in case f prefix reduces p to q at the monomial
 ,
we have
,
we have
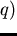 and p > q.
In case
and p > q.
In case  is the free monoid strong and prefix reduction coincide and are in fact Mora's reduction for treating right ideals in the free monoid ring.
The statements (1) to (3) of lemma 3.5 can
be carried over to prefix reduction.
But it is no longer true that
is the free monoid strong and prefix reduction coincide and are in fact Mora's reduction for treating right ideals in the free monoid ring.
The statements (1) to (3) of lemma 3.5 can
be carried over to prefix reduction.
But it is no longer true that
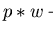 in case
in case
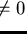 .
.
Example 3..16
Let
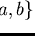
and
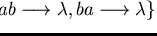
be a monoid presentation of a group

with a length-lexicographical ordering
induced by

.
Further let
![$p = a^2 + 1 \in {\bf Q}[{\cal G}]$](img316.gif)
.
Then
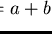
is not prefix reducible to
zero by
p.
As before, we can show that the translation lemma holds for prefix reduction.
Furthermore,
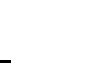 and
and
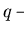 imply
imply
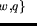 ,
i.e. the axioms (A1), (A2), (A3) and (A4) hold.
Unfortunately, prefix reduction need not capture the right ideal
congruence.
,
i.e. the axioms (A1), (A2), (A3) and (A4) hold.
Unfortunately, prefix reduction need not capture the right ideal
congruence.
Lemma 3..18
Let
![$p,q \in {\bf K}[{\cal M}]$](img298.gif)
and
![$F \subseteq {\bf K}[{\cal M}]$](img195.gif)
.
Then
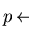
implies

but not vice versa.
Example 3..19
Let
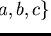
and

be a presentation of a group

with a length-lexicographical ordering induced by
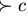
.
Inspecting the polynomials
![$p = a+b+c, q = b - \lambda\in{\bf Q}[{\cal G}]$](img328.gif)
and the set
![$F = \{ a+b+c \}\subseteq {\bf Q}[{\cal G}]$](img329.gif)
we get
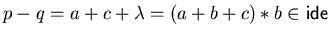
,
but
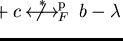
.
To prove this claim, let us assume
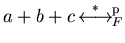
.
Then, since
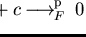
,
we get
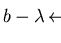
.
Let

be minimal such that
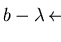
.
As
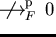
we know
n>1.
Thus, let us look at the sequence
where for all
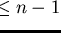
,
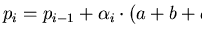
,
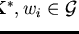
and
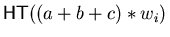
.
Further let
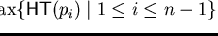
.
Then

,
as
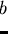
for all

such that
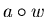
.
Let
pl be the first polynomial with
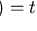
,
i.e.,

for all
j <
l,
and let
pl+k be the next polynomial,
where the occurrence of
t is changed.
Since
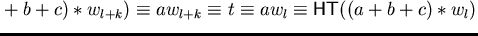
we can conclude
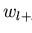
.
Further our transformation sequence is supposed to be of minimal length, i.e.,
t is not changed by the
reductions taking place in the sequence
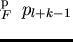
.
But then, eliminating
pl and substituting
pl+j by
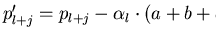
for all
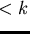
gives us a shorter sequence
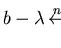
contradicting our assumption.
Obviously for a set of polynomials
![$F \subseteq {\bf K}[{\cal M}]$](img195.gif) we have
we have
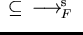 ,
but as seen in
example 3.19 in general we cannot expect
,
but as seen in
example 3.19 in general we cannot expect
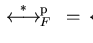 .
This can be gained by enriching the set F to a set F' such that
.
This can be gained by enriching the set F to a set F' such that
 and
and
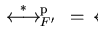 .
This will be achieved by a process called prefix saturation.
.
This will be achieved by a process called prefix saturation.
Definition 3..20
A set of polynomials
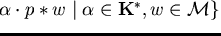
is called a
prefix saturating set for a non-zero polynomial
![$p\in
{\bf K}[{\cal M}]$](img360.gif)
,
if for all
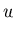
,
in case
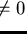
then
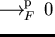
holds.
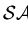
denotes the family of all prefix saturating sets for
p.
Definition 3..21
We call a set
![$F \subseteq {\bf K}[{\cal M}]$](img195.gif) prefix saturated
prefix saturated, if for all

and all
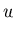
,
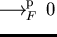
holds in case
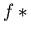
.
Note that in defining prefix saturating sets we demand prefix reducibility to 0 in one step.
This is done to have some equivalent for
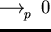 in Buchberger's approach and the fact that for strong right reduction
we have
in Buchberger's approach and the fact that for strong right reduction
we have
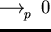 in case
in case
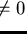 .
Other definitions of similar properties are possible and can be found
in [Ap88,Kr93,Re95].
.
Other definitions of similar properties are possible and can be found
in [Ap88,Kr93,Re95].
Of course there are procedures to enumerate prefix saturating sets of a polynomial p, since
the set
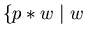 is recursively enumerable, and
it is decidable whether
is recursively enumerable, and
it is decidable whether
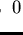 for some
for some
![$q \in {\bf K}[{\cal M}]$](img368.gif) and
and
![$F \subset {\bf K}[{\cal M}]$](img369.gif) finite.
But in general the set
finite.
But in general the set
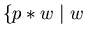 is infinite and,
hence, we have to look for
``suitable'' subsets and to find and compute finite ones in case they exist.
Note that prefix saturating sets for a polynomial p are prefix saturated.
A nice property of prefix saturated sets is that they
allow special representations of the elements belonging to
the right ideal they generate.
is infinite and,
hence, we have to look for
``suitable'' subsets and to find and compute finite ones in case they exist.
Note that prefix saturating sets for a polynomial p are prefix saturated.
A nice property of prefix saturated sets is that they
allow special representations of the elements belonging to
the right ideal they generate.
Lemma 3..22
Let
![$F \subseteq {\bf K}[{\cal M}]$](img195.gif)
be a prefix saturated set.
Then every non-zero polynomial
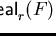
has a
representation of the form
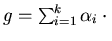
with
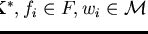
,
and
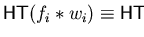
.
In fact using prefix reduction combined with prefix saturation we can
simulate strong right reduction and therefore we can then capture the
right ideal congruence.
Lemma 3..24
For a prefix saturated set
F of polynomials in
![${\bf K}[{\cal M}]$](img1.gif)
and
![$p,q \in {\bf K}[{\cal M}]$](img298.gif)
we have
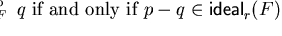
.
To enumerate prefix saturating sets for a polynomial, we can make use
of the fact that the elements of the monoid are represented by
words which are irreducible with respect to a convergent semi-Thue
system
 .
We do not have to compute all right monoid multiples of a polynomial
but we can restrict ourselves to those which are overlaps between the
respective head term of a polynomial multiple and the rules in T.
The following procedure uses this idea.
.
We do not have to compute all right monoid multiples of a polynomial
but we can restrict ourselves to those which are overlaps between the
respective head term of a polynomial multiple and the rules in T.
The following procedure uses this idea.
Procedure: PREFIX SATURATIONfont size=-1>PROTECT
< tex2html_comment_mark>
Given: A polynomial
![$p\in
{\bf K}[{\cal M}]$](img360.gif) and
and
 a convergent semi-Thue system presenting
a convergent semi-Thue system presenting  .
Find:
.
Find:
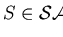 .
.
S :=  ;
H :=
;
H :=  ;
while
;
while
 do
q :=
do
q :=
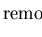 ;
% Remove an element using a fair strategy, i.e., no element is left in H for ever
t :=
;
% Remove an element using a fair strategy, i.e., no element is left in H for ever
t :=
 ;
for all
;
for all
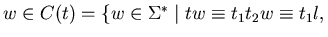 for some
for some
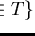 do
% C(t) contains special overlaps between t and left hand sides of rules in T
q' :=
do
% C(t) contains special overlaps between t and left hand sides of rules in T
q' :=  ;
if
;
if
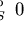 and
and 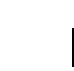 then S :=
then S :=
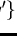 ;
H :=
;
H :=
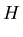 ;
endif
endfor
endwhile
;
endif
endfor
endwhile
Theorem 3..25
For a given polynomial
![$p\in
{\bf K}[{\cal M}]$](img360.gif)
,
let
S be the
set generated by procedure P
REFIX S
ATURATION.
Then for all
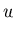
every non-zero polynomial

is prefix reducible to zero in one step using
S.
Hence, procedure PREFIX SATURATION enumerates a prefix
saturating set for a polynomial and we find:
Lemma 3..26
In case a polynomial has a finite prefix saturating set, then
procedure P
REFIX S
ATURATION terminates.
This is the case e.g. for monoids with a finite convergent monadic presentation.
Similar to definition 3.8 we can define Gröbner bases with
respect to prefix reduction.
Definition 3..27
A set
![$G \subseteq {\bf K}[{\cal M}]$](img250.gif)
is said to be a
prefix Gröbner basis of
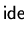
,
if
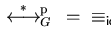
,
and

is confluent.
Notice that prefix saturating sets for a polynomial p satisfy the
first statement of this definition,
but in general need not be prefix
Gröbner bases of
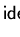 ,
i.e., the elements of
,
i.e., the elements of
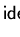 do not necessarily prefix reduce to zero.
do not necessarily prefix reduce to zero.
Example 3..28
Reviewing example
3.19, let
p =
a +
b +
c.
Then
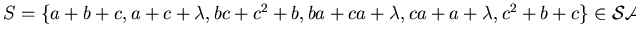
,
but

is not confluent on
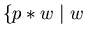
.
We have
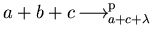
and
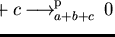
but
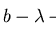
.
This example also shows that Gröbner bases via
 are Gröbner bases
via
are Gröbner bases
via
 but not vice versa.
The set
but not vice versa.
The set
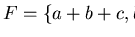 is a strong Gröbner basis, but
not a prefix Gröbner basis.
Remember that prefix saturation enriches a polynomial p to a set
is a strong Gröbner basis, but
not a prefix Gröbner basis.
Remember that prefix saturation enriches a polynomial p to a set
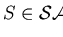 such that we can
substitute
such that we can
substitute
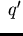 by
by
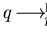 .
We use this additional information to give a confluence
criterion that will use a refined
definition of s-polynomials.
.
We use this additional information to give a confluence
criterion that will use a refined
definition of s-polynomials.
Definition 3..29
Given two non-zero polynomials
![$p_{1}, p_{2} \in {\bf K}[{\cal M}]$](img267.gif)
,
if there is
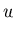
such that

the
prefix
s-polynomial is defined as
As before non-zero prefix s-polynomials are called non-trivial.
In case an s-polynomial exists
we always
have
 .
Notice that a finite set
.
Notice that a finite set
![$F \subseteq {\bf K}[{\cal M}]$](img195.gif) defines
finitely many prefix s-polynomials and the following lemma enables us to localize our confluence test to these s-polynomials.
defines
finitely many prefix s-polynomials and the following lemma enables us to localize our confluence test to these s-polynomials.
Lemma 3..30
Let
F be a set of polynomials in
![${\bf K}[{\cal M}]$](img1.gif)
and
![$p\in
{\bf K}[{\cal M}]$](img360.gif)
.
Further let
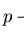
and let us assume this reduction sequence results
in a representation
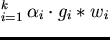
,
where
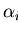
,

,
and
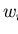
.
Then for every term
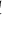
such that
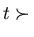
and
every term
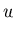
we get that if
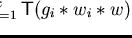
then
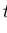
holds.
Prefix s-polynomials alone are not sufficient to
characterize prefix Gröbner
bases, but
in case we demand our set of polynomials to be prefix saturated we
can give a characterization similar to theorem 3.13.
Corollary 3..32
A prefix saturated set
![$F \subseteq {\bf K}[{\cal M}]$](img195.gif)
is a prefix
Gröbner basis of
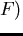
if and only if
for all
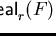
we have
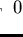
.
Now theorem 3.31 gives rise to the following procedure, which can be modified to enumerate a Gröbner
basis with respect to
 for a finitely generated
right ideal.
Termination will be shown for some special cases where finite prefix
saturated Gröbner bases exist in the next section.
for a finitely generated
right ideal.
Termination will be shown for some special cases where finite prefix
saturated Gröbner bases exist in the next section.
Procedure: PREFIX GR¨OBNER BASESfont size=-1>PROTECT
< tex2html_comment_mark>
Given: A finite set of polynomials
![$F \subseteq {\bf K}[{\cal M}]$](img195.gif) ,
and
,
and
 a convergent semi-Thue system presenting
a convergent semi-Thue system presenting  .
Find:
.
Find:
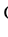 a prefix Gröbner basis of F.
Using:
a prefix Gröbner basis of F.
Using:
 a prefix saturating procedure for polynomials.
a prefix saturating procedure for polynomials.
G :=
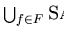 ;
% G is prefix saturated
B :=
;
% G is prefix saturated
B :=
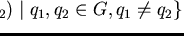 ;
while
;
while
 do
% Test if statement 2 of theorem 3.31 is valid
(q1, q2) := remove(B);
% Remove an element using a fair strategy
if
do
% Test if statement 2 of theorem 3.31 is valid
(q1, q2) := remove(B);
% Remove an element using a fair strategy
if
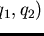 exists
% The s-polynomial is not trivial
then h:= normal form
exists
% The s-polynomial is not trivial
then h:= normal form
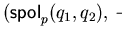 ;
% Compute a normal form using prefix reduction
if
;
% Compute a normal form using prefix reduction
if  then G :=
then G :=
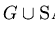 ;
% G is prefix saturated
B :=
;
% G is prefix saturated
B :=
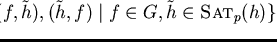 ;
endif
endif
endwhile
;
endif
endif
endwhile
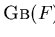
There are two crucial points, why procedure PREFIX GR¨OBNER BASES
might not terminate:
prefix saturation of a polynomial need not terminate
and the set B need not become empty.
In the next section certain groups with very simple finite
prefix saturating sets are presented.
Notice that in case prefix saturation does not terminate it is possible
to modify this procedure in order to enumerate a prefix Gröbner
basis by using fair enumerations of the prefix saturating sets
needed.
This results in a more technical procedure.
Termination of procedure PREFIX GR¨OBNER BASES
can be shown e.g. for finite convergent special monoid or
monadic group presentations.
More details on this subject are provided in the next section.
In the following example we want to illustrate how procedure PREFIX GR¨OBNER BASES works by computing a prefix Gröbner basis of the right ideal
specified in example 3.10.
Example 3..33
Let
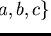
and

with a length-lexicographical ordering induced by
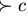
.
We want to compute a prefix Gröbner basis of
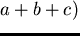
.
On initializing
G we get
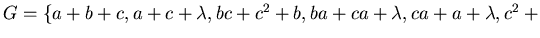
(compare example
3.28).
Now inspecting this set we see that only one prefix s-polynomial has to be considered, namely
Since
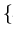
is a saturating set for the polynomial

we
get
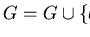
.
Now there are two possible prefix s-polynomials to consider and we find
respectively
and hence
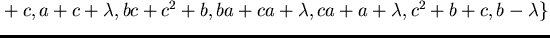
is a prefix Gröbner basis of
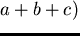
.
Furthermore, theorem 3.31 characterizes prefix saturated prefix
Gröbner bases.
But prefix Gröbner bases need not be prefix saturated.
In [Re95] we have hence given other characterizations of
prefix Gröbner bases and introduced the concept of interreduction
to the theory.
Using those results we can even state that for
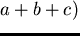 in example 3.33 the set
in example 3.33 the set
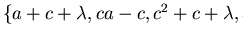 is a reduced
prefix Gröbner basis.
We close this section by showing how similar to the case of solvable polynomial rings ([Kr93,KaWe90]), Gröbner bases of two-sided
ideals can be characterized by prefix reduction and prefix Gröbner bases which have
additional properties.
We will call a set of polynomials a Gröbner basis of the
two-sided ideal it generates, if it fulfills one of the equivalent
statements in the next theorem.
is a reduced
prefix Gröbner basis.
We close this section by showing how similar to the case of solvable polynomial rings ([Kr93,KaWe90]), Gröbner bases of two-sided
ideals can be characterized by prefix reduction and prefix Gröbner bases which have
additional properties.
We will call a set of polynomials a Gröbner basis of the
two-sided ideal it generates, if it fulfills one of the equivalent
statements in the next theorem.
Statement 4 enables a constructive approach to extend procedure PREFIX GR¨OBNER BASES in order to enumerate
prefix Gröbner bases of two-sided ideals (and in fact in case
prefix saturation always terminates this procedure will compute finite
prefix saturated Gröbner bases in case they exist).
Item 2 states how prefix Gröbner bases are
related to the membership problem for two-sided ideals.
In this case if
![${\bf K}[{\cal M}]$](img1.gif) is a right reduction ring and G is a finite
prefix Gröbner basis of
is a right reduction ring and G is a finite
prefix Gröbner basis of
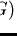 ,
then
,
then
![${\bf K}[{\cal M}]/{\sf ideal}_{}^{}(G)$](img444.gif) is a right reduction ring.
is a right reduction ring.



Next: 4. Group Rings
Up: String Rewriting and Gröbner
Previous: 2. Fundamental Relations Between
| ZCA Home |
Reports |
 is the
coefficient of this term and
is the
coefficient of this term and
 is the set of terms occurring in
p.
The ordering on
is the set of terms occurring in
p.
The ordering on  .
Suppose we simply require divisibility10 of the head term to allow reduction.
Then we could reduce the
polynomial
.
Suppose we simply require divisibility10 of the head term to allow reduction.
Then we could reduce the
polynomial
 of p in one step, denoted by
of p in one step, denoted by
 .
. ,
then
,
then
 one has to decide whether
there exist elements
one has to decide whether
there exist elements
 .
Then the equation
.
Then the equation
 ,
and
the equation
,
and
the equation
 .
Furthermore, let
f1,
f2, p be polynomials in
.
Furthermore, let
f1,
f2, p be polynomials in
![${\bf Q}[{\cal M}]$](img211.gif) such that
f1 = a2 + a,
f2 = a2
- a and
such that
f1 = a2 + a,
f2 = a2
- a and
 or a strong Gröbner
basis of
or a strong Gröbner
basis of
![]() to the
equations in two variables of the form
to the
equations in two variables of the form
![]() where
where
![]() and
and
![]() .
It can be empty, finite or even infinite.
We can now give a criterion that implies confluence
for strong right reduction in terms of strong s-polynomials.
.
It can be empty, finite or even infinite.
We can now give a criterion that implies confluence
for strong right reduction in terms of strong s-polynomials.![]() is decidable.
is decidable.
, and
a convergent semi-Thue system presenting
. Question: Does there exist a strong s-polynomial for p and q?
![]() and
and
![]() on a set
on a set ![]() such that
such that
![]() and
and
![]() ,
the confluence of
,
the confluence of
![]() on
on ![]() implies the
confluence of
implies the
confluence of
![]() on
on ![]() .
.
![]() .
Notice that such prefixes are divisors with respect to word concatenation
and hence easy to determine.
.
Notice that such prefixes are divisors with respect to word concatenation
and hence easy to determine. of p in one step, denoted by
of p in one step, denoted by
 is a prefix of t, and
is a prefix of t, and
 if there is a polynomial q as defined
above and p is then called prefix reducible by f.
Prefix reduction by a set
if there is a polynomial q as defined
above and p is then called prefix reducible by f.
Prefix reduction by a set
 .
. ,
we have
,
we have
 .
Further let
.
Further let
 and
and
 ,
as
,
as
 and all
and all
![]() is recursively enumerable, and
it is decidable whether
is recursively enumerable, and
it is decidable whether
![]() for some
for some
![]() and
and
![]() finite.
But in general the set
finite.
But in general the set
![]() is infinite and,
hence, we have to look for
``suitable'' subsets and to find and compute finite ones in case they exist.
Note that prefix saturating sets for a polynomial p are prefix saturated.
A nice property of prefix saturated sets is that they
allow special representations of the elements belonging to
the right ideal they generate.
is infinite and,
hence, we have to look for
``suitable'' subsets and to find and compute finite ones in case they exist.
Note that prefix saturating sets for a polynomial p are prefix saturated.
A nice property of prefix saturated sets is that they
allow special representations of the elements belonging to
the right ideal they generate.and
a convergent semi-Thue system presenting
. Find:
.
; H :=
; while
do q :=
; % Remove an element using a fair strategy, i.e., no element is left in H for ever t :=
; for all
for some
do % C(t) contains special overlaps between t and left hand sides of rules in T q' :=
; if
and
then S :=
; H :=
; endif endfor endwhile
 is prefix reducible to zero in one step using S.
is prefix reducible to zero in one step using S. is confluent.
is confluent. is not confluent on
is not confluent on
 but not vice versa.
The set
but not vice versa.
The set
, and
a convergent semi-Thue system presenting
. Find:
a prefix Gröbner basis of F. Using:
a prefix saturating procedure for polynomials.
; % G is prefix saturated B :=
; while
do % Test if statement 2 of theorem 3.31 is valid (q1, q2) := remove(B); % Remove an element using a fair strategy if
exists % The s-polynomial is not trivial then h:= normal form
; % Compute a normal form using prefix reduction if
then G :=
; % G is prefix saturated B :=
; endif endif endwhile
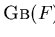
 we
get
we
get
![]() in example 3.33 the set
in example 3.33 the set
![]() is a reduced
prefix Gröbner basis.
We close this section by showing how similar to the case of solvable polynomial rings ([Kr93,KaWe90]), Gröbner bases of two-sided
ideals can be characterized by prefix reduction and prefix Gröbner bases which have
additional properties.
We will call a set of polynomials a Gröbner basis of the
two-sided ideal it generates, if it fulfills one of the equivalent
statements in the next theorem.
is a reduced
prefix Gröbner basis.
We close this section by showing how similar to the case of solvable polynomial rings ([Kr93,KaWe90]), Gröbner bases of two-sided
ideals can be characterized by prefix reduction and prefix Gröbner bases which have
additional properties.
We will call a set of polynomials a Gröbner basis of the
two-sided ideal it generates, if it fulfills one of the equivalent
statements in the next theorem. we have
we have
 ,
,
 we have
we have