next up previous
Next: About this document ... Up: Monomial Representations for Gröbner Computations Previous: Appendix A: Benchmark examples

Appendix B: Timings on other machines







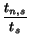Example tn,s %mon %comp %div %add $\displaystyle \frac{t_{n,s}}{t_s}$ $\displaystyle \frac{t_{n,c}}{t_c}$ $\displaystyle \frac{t_s}{t_c}$ $\displaystyle \frac{t_{1.0}}{t_{n,s}}$ $\displaystyle \frac{t_{1.0}}{t_c} $
homog alex 2 10.6 74.0 62.5 5.9 5.6 1.5 1.3 0.9 3.3 4.6
ecyclic 6 3.9 72.4 66.9 2.0 3.5 1.5 1.8 1.2 1.3 2.3
katsura 7 6.9 69.3 47.4 4.2 17.7 1.4 1.8 1.3 2.0 3.6
katsura 8 89.4 71.1 53.3 3.5 14.2 1.4 1.6 1.2 1.9 3.3
alex 3 1.7 68.0 57.7 8.6 1.7 1.4 1.3 1.0 3.2 4.3
gerhard 1 1.4 68.5 55.1 6.0 7.4 1.4 1.5 1.1 2.9 4.2
cohn2 9.3 66.1 37.2 5.0 23.9 1.4 1.6 1.2 1.7 2.8
2mat3 161.0 79.7 76.9 1.5 1.4 1.3 1.4 1.4 1.7 3.1
alex 2 5.9 69.2 59.9 3.6 5.7 1.3 1.6 1.4 3.1 5.6
homog gonnet 154.0 79.8 49.5 29.1 1.2 1.3 1.5 1.7 1.6 3.5
homog 2mat3 158.7 81.3 78.2 1.6 1.4 1.3 1.5 1.5 1.8 3.5
rcyclic 14 20.4 73.7 27.2 36.5 10.0 1.3 1.5 1.4 1.5 2.7
ecyclic 7 1260.3 85.4 83.8 0.3 1.2 1.3 1.4 1.2 1.3 1.9
homog alex 3 1.8 66.5 51.8 12.3 2.3 1.3 1.1 0.9 2.9 3.3
bjork 8 3.9 57.6 33.0 11.6 13.0 1.3 1.6 1.5 1.6 2.9
rcyclic 12 3.3 69.6 28.2 30.4 11.0 1.2 1.7 1.3 1.7 2.7
homog cyclic 7 147.8 74.9 36.1 22.0 16.7 1.2 1.5 1.3 1.5 2.5
rcyclic 13 8.0 70.1 30.9 30.2 9.1 1.2 1.4 1.1 1.7 2.3
homog cyclic 6 0.7 63.5 28.8 22.0 12.7 1.2 1.7 1.4 1.7 2.9
gerhard 2 11.0 71.4 58.8 3.0 9.6 1.2 1.9 1.6 3.4 6.6
schwarz 10 24.9 56.0 29.9 17.0 9.2 1.2 1.3 1.3 1.4 2.2
rcyclic 16 112.0 77.4 29.1 36.8 11.5 1.2 1.6 1.5 1.4 2.6
schwarz 9 3.1 58.4 31.4 21.1 5.9 1.2 1.3 1.1 1.5 1.9
cyclic 7 226.8 59.8 30.2 13.2 16.4 1.2 1.4 1.3 1.5 2.3
rcyclic 17 233.6 78.0 29.7 36.7 11.6 1.2 1.4 1.3 1.5 2.3
rcyclic 11 1.3 64.4 25.3 28.4 10.7 1.2 1.5 1.3 1.6 2.4
rcyclic 15 50.0 74.1 27.6 35.8 10.8 1.2 1.6 1.6 1.5 2.9
schwarz 8 0.6 50.0 30.2 12.3 7.6 1.2 1.4 1.2 1.4 2.0
rcyclic 19 916.6 79.8 29.4 38.9 11.6 1.1 1.5 1.5 1.4 2.4
gerhard 3 28.6 61.9 43.8 12.3 5.8 1.1 1.4 1.2 2.4 3.4
rcyclic 18 477.2 79.6 28.6 39.4 11.6 1.1 1.4 1.5 1.4 2.4
symmetric 6 74.0 70.8 28.2 24.0 18.6 1.1 1.3 1.2 1.5 2.0
gonnet 1.1 56.7 12.7 40.8 3.2 1.1 1.1 1.1 1.1 1.4
schwarz 11 178.2 60.1 34.4 16.8 9.0 1.1 1.3 1.4 1.4 2.1
averages
HP C160 125.4 69.0 41.7 17.9 9.5 1.2 1.5 1.3 1.8 2.9
Pentium Pro 103.3 69.8 38.4 15.6 15.8 1.4 1.6 1.2 1.2 2.2
DEC Alpha 221.4 69.8 37.7 16.1 16.0 1.7 1.7 1.2 1.1 2.3
 


 
Table 5: Detailed timings for vectorized monomial operations for DEC Alpha (64 bit, little-endian) running Linux.
Example tn,s %mon %comp %div %add $\displaystyle \frac{t_{n,s}}{t_s}$ $\displaystyle \frac{t_{n,c}}{t_c}$ $\displaystyle \frac{t_s}{t_c}$ $\displaystyle \frac{t_{1.0}}{t_{n,s}}$ $\displaystyle \frac{t_{1.0}}{t_c} $
rcyclic 12 10.1 74.8 28.2 28.1 18.5 2.1 2.2 1.3 1.1 3.0
ecyclic 6 9.4 69.1 60.7 1.6 6.8 2.0 2.2 1.3 1.2 3.2
rcyclic 11 3.8 68.4 26.1 24.8 17.4 2.0 2.0 1.2 1.1 2.7
rcyclic 15 124.6 80.9 30.3 31.0 19.6 2.0 2.4 1.4 1.2 3.2
homog cyclic 6 2.0 69.9 30.2 15.6 24.1 2.0 2.1 1.2 1.1 2.7
rcyclic 19 1838.3 83.8 30.6 31.8 21.4 2.0 2.0 1.2 1.1 2.6
rcyclic 14 55.0 79.7 29.5 31.1 19.2 1.9 2.3 1.4 1.2 3.1
rcyclic 13 24.9 77.9 30.3 28.1 19.5 1.9 2.3 1.4 1.1 3.1
rcyclic 18 986.4 84.5 30.7 34.6 19.2 1.9 1.9 1.2 1.1 2.6
rcyclic 16 256.6 82.3 30.5 32.1 19.8 1.9 2.0 1.2 1.2 2.7
katsura 7 21.1 71.1 41.4 3.9 25.9 1.9 1.6 1.0 1.1 2.1
homog gonnet 310.1 81.1 44.9 33.9 2.3 1.9 1.9 1.1 1.2 2.4
bjork 8 10.1 69.0 33.0 12.6 23.4 1.9 1.8 1.1 1.0 2.1
homog cyclic 7 300.2 77.9 37.4 13.2 27.4 1.8 1.8 1.1 1.2 2.4
rcyclic 17 527.1 83.2 30.4 33.3 19.5 1.8 1.9 1.2 1.1 2.5
cyclic 7 458.9 68.6 32.5 10.3 25.7 1.7 1.7 1.2 1.1 2.1
cyclic 6 1.7 61.4 25.3 13.5 22.6 1.7 1.7 1.2 1.0 2.0
ecyclic 7 1805.0 60.7 55.9 0.6 4.2 1.7 1.8 1.1 1.2 2.4
homog 2mat3 256.8 78.3 74.1 1.8 2.5 1.7 1.8 1.2 1.4 2.6
gerhard 1 4.0 71.2 50.5 5.4 15.2 1.6 1.6 1.2 1.3 2.4
katsura 8 229.9 73.3 46.6 3.0 23.7 1.6 1.7 1.2 1.1 2.2
gonnet 2.8 51.7 8.2 40.4 3.1 1.6 1.6 1.1 1.0 1.7
cohn2 24.6 65.9 30.3 3.2 32.4 1.6 1.5 1.2 1.0 1.9
schwarz 8 1.3 50.0 19.6 14.9 15.4 1.6 1.5 1.0 1.0 1.7
schwarz 11 317.1 65.4 32.4 16.5 16.4 1.6 1.6 1.1 1.1 1.9
schwarz 10 51.2 62.9 29.4 17.3 16.2 1.5 1.6 1.1 1.1 1.9
symmetric 6 147.2 72.4 29.1 13.8 29.5 1.5 1.5 1.2 1.1 2.1
homog alex 2 32.1 74.8 60.6 4.4 9.7 1.5 1.5 1.2 1.3 2.3
schwarz 9 7.5 57.9 23.6 17.8 16.5 1.5 1.6 1.1 1.1 1.9
gerhard 2 33.2 72.7 56.2 2.1 14.3 1.5 1.4 1.2 1.3 2.3
2mat3 248.0 70.5 66.4 1.6 2.4 1.4 1.5 1.2 1.2 2.0
alex 2 17.4 65.1 52.6 2.9 9.6 1.4 1.2 1.1 1.1 1.7
homog alex 3 5.2 65.5 48.7 12.5 4.3 1.3 1.3 1.1 1.2 1.8
gerhard 3 61.4 66.6 46.7 9.7 10.2 1.3 1.3 1.2 1.2 1.9
alex 3 4.4 60.8 50.1 6.3 4.5 1.2 1.2 1.1 1.2 1.7
averages
DEC Alpha 221.4 69.8 37.7 16.1 16.0 1.7 1.7 1.2 1.1 2.3
Pentium Pro 103.3 69.8 38.4 15.6 15.8 1.4 1.6 1.2 1.2 2.2
HP C160 125.4 69.0 41.7 17.9 9.5 1.2 1.5 1.3 1.8 2.9
 


 
Table 6: Detailed timings for rank-based monomial operations on an HP C160 (32 bit, big-endian) running HP-UX 10.20.
exponent type char short short
monomial operations vectorized vectorized not vectorized
Example $\displaystyle \frac{t_{<}}{t_{r,<}}$ %R %comp $\displaystyle \frac{t}{t_{r}}$ $\displaystyle \frac{t_{<}}{t_{r,<}}$ %R %comp $\displaystyle \frac{t}{t_{r}}$ $\displaystyle \frac{t_{<}}{t_{r,<}}$ %R %comp $\displaystyle \frac{t}{t_{r}}$
2mat3 1.3 2.6 75.5 1.0 1.2 2.1 75.3 1.1 1.2 1.8 78.1 1.4
homog alex 2 1.4 6.8 56.1 1.0 1.7 6.4 58.9 0.9 1.9 7.9 61.4 1.3
alex 3 1.5 3.3 48.2 1.0 1.4 1.4 55.9 0.9 1.5 3.1 58.0 1.3
alex 2 1.6 5.7 56.0 0.8 1.5 5.6 60.2 1.0 1.4 5.9 57.7 1.2
katsura 8 1.6 13.4 48.6 0.9 1.6 12.5 50.5 1.0 2.0 13.7 54.4 1.2
homog alex 3 1.9 2.6 49.9 1.1 2.1 1.8 50.9 1.0 1.9 4.2 46.6 1.2
homog gonnet 1.7 2.5 42.6 0.9 1.4 1.6 45.2 1.1 1.6 1.6 48.4 1.2
gerhard 1 1.7 7.7 55.5 0.9 1.5 9.5 51.9 0.9 2.3 12.9 56.6 1.2
katsura 7 1.6 17.6 39.6 0.8 1.9 16.2 49.1 0.9 1.8 15.9 48.2 1.2
gerhard 2 1.4 8.2 55.0 0.7 1.7 9.7 61.4 1.0 1.6 9.3 57.5 1.1
homog 2mat3 1.3 2.7 76.8 0.9 1.0 1.7 76.6 1.0 1.2 1.9 78.0 1.1
cyclic 7 1.3 10.7 25.0 0.9 1.5 10.6 25.4 0.9 1.8 12.1 30.1 1.1
gerhard 3 1.4 4.8 36.2 0.9 1.7 5.4 39.4 1.0 1.6 5.5 40.7 1.1
schwarz 11 1.2 7.8 30.4 0.9 1.3 6.4 30.5 1.0 1.5 7.2 34.0 1.1
bjork 8 1.1 10.6 23.2 0.8 1.7 10.5 33.7 0.9 2.2 12.5 32.8 1.0
schwarz 10 1.5 8.8 26.7 0.9 1.3 7.1 24.7 0.9 1.6 9.3 30.7 1.0
homog cyclic 7 1.4 11.9 27.7 0.8 1.8 11.2 29.7 0.9 2.0 12.5 34.3 1.0
cohn2 1.2 12.6 28.9 0.7 1.6 13.7 31.8 0.8 1.9 15.8 35.1 1.0
rcyclic 13 2.0 14.1 24.0 0.8 1.8 10.9 25.7 0.9 2.9 12.0 29.5 1.0
rcyclic 12 1.6 11.3 18.8 0.8 1.9 9.7 22.6 0.8 2.4 11.4 28.4 1.0
rcyclic 14 2.0 12.0 23.4 0.8 1.6 10.8 20.9 0.8 2.5 10.3 28.7 1.0
rcyclic 15 1.4 12.1 23.1 0.8 1.5 9.3 23.3 0.9 1.5 9.8 28.3 1.0
schwarz 9 1.7 11.7 23.5 0.9 1.6 13.5 23.4 0.9 2.5 12.0 28.4 1.0
symmetric 6 1.3 10.9 21.8 0.8 1.4 11.3 24.9 0.9 1.8 13.6 28.9 1.0
homog cyclic 6 1.0 9.6 24.5 0.7 2.3 16.9 29.1 0.8 2.6 17.5 25.4 1.0
schwarz 8 1.4 10.9 15.7 0.8 1.9 9.5 23.3 0.9 2.9 5.9 21.7 1.0
rcyclic 11 2.0 13.0 26.9 0.8 2.2 7.2 22.3 0.8 2.6 14.9 29.0 1.0
gonnet 1.0 5.0 3.5 0.9 2.2 4.0 9.6 0.9 1.0 4.1 6.4 1.0
cyclic 6 0.8 13.8 16.5 0.8 2.5 15.5 24.1 0.8 1.7 17.0 32.4 1.0
ecyclic 7 1.0 2.5 85.3 0.9 1.0 1.8 83.9 0.9 0.8 1.2 84.8 0.9
rcyclic 19 1.1 9.6 23.7 0.8 1.0 7.3 24.2 0.8 0.8 6.5 29.5 0.9
ecyclic 6 1.1 16.7 61.7 0.7 1.1 11.2 62.2 0.8 0.6 9.2 67.8 0.8
rcyclic 18 0.9 9.0 22.7 0.9 0.9 7.8 23.6 0.8 0.9 7.0 28.3 0.8
rcyclic 16 1.1 11.1 23.2 0.7 1.2 9.4 24.1 0.8 0.8 8.0 29.0 0.8
rcyclic 17 1.0 9.4 22.1 0.8 0.9 8.1 24.9 0.8 1.1 8.1 30.1 0.8
averages    
HP C160 1.4 9.1 36.6 0.8 1.6 8.4 39.0 0.9 1.7 9.1 41.6 1.1
Pentium Pro 1.3 17.1 33.6 0.8 1.4 13.8 33.8 0.9 2.1 12.6 40.3 1.1
DEC Alpha 1.8 11.8 33.1 0.8 1.5 11.7 31.5 0.8 2.4 10.2 35.5 1.0
 


 
Table 7: Detailed timings for rank-based monomial operations on a DEC Alpha (64 bit, little-endian) running Linux.
exponent type char short short
monomial operations vectorized vectorized not vectorized
Example $\displaystyle \frac{t_{<}}{t_{r,<}}$ %R %comp $\displaystyle \frac{t}{t_{r}}$ $\displaystyle \frac{t_{<}}{t_{r,<}}$ %R %comp $\displaystyle \frac{t}{t_{r}}$ $\displaystyle \frac{t_{<}}{t_{r,<}}$ %R %comp $\displaystyle \frac{t}{t_{r}}$
homog alex 2 2.4 9.7 60.7 1.0 2.0 9.3 56.4 1.0 2.6 8.8 59.4 1.4
homog alex 1 2.2 5.7 55.9 1.3 1.6 5.5 44.0 1.1 2.2 5.6 48.6 1.3
homog gonnet 1.3 5.0 41.1 1.1 1.7 5.2 45.6 1.1 2.9 4.4 44.7 1.3
alex 1 1.7 2.4 65.2 1.3 1.5 3.2 62.8 1.3 1.4 2.7 59.9 1.3
homog 2mat3 1.7 2.4 65.2 1.3 1.5 3.2 62.8 1.3 1.4 2.7 59.9 1.3
gerhard 2 2.1 10.8 57.8 0.9 1.7 10.1 53.0 1.0 2.1 10.2 53.6 1.3
alex 2 1.6 8.6 56.6 1.1 1.4 7.3 54.6 1.2 1.6 6.9 56.1 1.3
gerhard 1 2.4 13.4 51.3 0.8 1.8 12.8 45.1 0.9 2.3 11.8 48.1 1.3
gerhard 3 1.9 7.4 44.1 1.0 1.5 7.2 40.8 1.0 1.9 7.0 44.3 1.2
homog alex 3 1.9 4.6 50.2 1.0 1.6 5.0 46.2 1.1 2.0 5.2 49.1 1.2
alex 3 1.4 5.4 53.5 1.0 1.3 5.3 51.8 1.0 1.7 5.5 55.5 1.2
katsura 8 1.7 19.8 47.1 0.8 1.7 17.9 44.8 0.9 2.9 17.4 46.9 1.2
katsura 7 1.7 20.1 39.4 0.8 1.7 19.0 36.8 0.8 2.8 17.2 41.0 1.1
cyclic 7 2.0 17.1 27.6 0.8 1.5 17.1 26.5 0.8 2.7 15.0 32.8 1.1
bjork 8 1.8 17.8 26.0 0.8 1.6 16.7 25.8 0.8 3.0 16.4 32.1 1.1
homog cyclic 7 1.7 17.1 29.7 0.7 1.8 18.2 29.2 0.7 3.0 16.2 35.0 1.1
cohn2 2.4 19.7 30.4 0.8 1.4 15.8 24.5 0.9 2.1 14.5 29.9 1.1
schwarz 11 1.7 14.7 31.0 0.8 1.6 16.0 30.5 0.9 2.4 13.3 32.9 1.0
rcyclic 14 1.7 20.7 24.8 0.6 2.0 21.9 24.9 0.7 3.8 15.7 28.7 1.0
rcyclic 13 1.8 20.4 20.9 0.7 2.0 21.1 23.6 0.7 3.9 16.1 28.9 1.0
symmetric 6 2.0 16.4 26.1 0.7 1.5 16.1 21.6 0.8 2.4 14.3 27.1 1.0
cyclic 6 2.9 19.3 23.5 0.7 1.3 16.7 16.5 0.7 2.6 14.5 25.3 1.0
schwarz 10 1.7 14.3 25.9 0.8 1.6 17.1 25.3 0.9 2.4 13.4 29.7 1.0
schwarz 8 1.8 13.3 13.4 0.7 1.8 12.8 15.6 0.7 2.7 12.5 19.3 1.0
symmetric 5 2.1 13.8 18.5 0.8 1.3 11.4 11.8 0.8 2.2 12.2 17.5 1.0
homog cyclic 6 2.7 18.2 26.7 0.6 1.7 19.2 20.5 0.6 3.2 19.1 26.8 1.0
rcyclic 11 1.9 17.2 19.4 0.6 1.9 20.0 19.2 0.6 3.6 15.3 25.5 1.0
rcyclic 15 1.5 15.6 26.0 0.7 1.6 16.1 25.2 0.8 2.3 12.2 29.9 1.0
rcyclic 12 1.9 19.9 22.1 0.7 1.9 20.1 22.2 0.7 3.7 15.5 27.7 1.0
ecyclic 7 1.9 19.9 22.1 0.7 1.9 20.1 22.2 0.7 3.7 15.5 27.7 1.0
schwarz 9 1.6 15.2 19.7 0.8 1.6 14.0 18.9 0.8 2.8 13.7 23.8 0.9
gonnet 1.4 9.1 4.4 0.8 1.3 9.8 5.0 0.8 3.1 6.8 8.3 0.9
rcyclic 10 2.8 16.2 13.8 0.6 2.0 18.8 14.6 0.7 4.2 15.3 20.2 0.9
ecyclic 6 0.9 1.0 57.7 0.6 0.9 1.1 57.3 0.7 1.0 0.8 67.3 0.9
rcyclic 18 0.9 1.0 23.4 0.7 1.0 1.1 28.6 0.7 1.0 0.6 31.8 0.8
rcyclic 19 1.1 1.0 25.8 0.7 1.0 1.1 24.8 0.7 0.9 1.0 28.8 0.8
rcyclic 17 0.9 1.5 21.5 0.7 1.0 1.6 25.6 0.7 1.0 1.0 29.5 0.8
rcyclic 16 0.9 3.3 21.3 0.7 1.0 3.3 24.7 0.7 1.1 2.2 29.9 0.8

averages

    
DEC Alpha 1.8 11.8 33.1 0.8 1.5 11.7 31.5 0.8 2.4 10.2 35.5 1.0
Pentium Pro 1.3 17.1 33.6 0.8 1.4 13.8 33.8 0.9 2.1 12.6 40.3 1.1
HP C160 1.4 9.1 36.6 0.8 1.6 8.4 39.0 0.9 1.7 9.1 41.6 1.1
 

next up previous
Next: About this document ... Up: Monomial Representations for Gröbner Computations Previous: Appendix A: Benchmark examples
| ZCA Home | Reports |