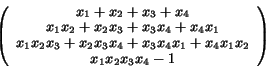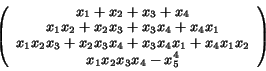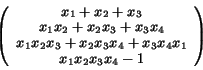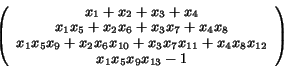Next: Appendix B: Timings on
Up: Monomial Representations for Gröbner Computations
Previous: Bibliography
I this appendix, we show some more details about the sets of
polynomial we used for our GB computation test runs.
Table 3:
Summary of properties of benchmark examples
| Example |
#vars |
#polys |
homog |
Degs |
Deg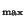 |
Ref |
| ecyclic 7 |
43 |
7 |
no |
7 |
27 |
|
| ecyclic 6 |
31 |
6 |
no |
6 |
17 |
|
rcyclic
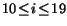 |
i |
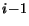 |
no |
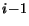 |
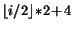 |
|
| homog 2mat3 |
19 |
8 |
yes |
4 |
13 |
[14] |
| 2mat3 |
18 |
8 |
no |
4 |
13 |
|
| homog gonnet |
18 |
19 |
yes |
2 |
11 |
[6] |
| gonnet |
17 |
19 |
no |
2 |
11 |
[6] |
| schwarz 11 |
11 |
11 |
no |
2 |
13 |
|
| schwarz 10 |
10 |
10 |
no |
2 |
12 |
|
| katsura 8 |
9 |
9 |
no |
2 |
10 |
[13] |
| katsura 7 |
8 |
8 |
no |
2 |
9 |
[13] |
| bjork 8 |
8 |
9 |
no |
8 |
18 |
[5] |
| homog cyclic 7 |
8 |
7 |
yes |
7 |
20 |
[5] |
| cyclic 7 |
7 |
7 |
no |
7 |
27 |
[5] |
| homog cyclic 6 |
7 |
6 |
yes |
6 |
17 |
[5] |
| cyclic 6 |
6 |
6 |
no |
6 |
17 |
[5] |
| homog alex 3 |
6 |
4 |
yes |
14 |
51 |
|
| alex 3 |
5 |
4 |
no |
14 |
51 |
|
| gerhard 1 |
5 |
3 |
yes |
10 |
32 |
|
| symmetric 6 |
5 |
5 |
yes |
6 |
23 |
[12] |
| homog alex 2 |
5 |
3 |
yes |
12 |
40 |
|
| cohn2 |
4 |
4 |
no |
6 |
20 |
[14] |
| alex 2 |
4 |
3 |
no |
12 |
33 |
|
| gerhard 2 |
4 |
3 |
yes |
9 |
44 |
|
| gerhard 3 |
4 |
3 |
yes |
23 |
81 |
|
|
Table
3 lists a summary of their properties: column
#vars shows the number of occurring variables, column
#polys the number of elements (polynomials), column
homog gives the homogeneity, and Degs shows the maximal
degree of the input sets. Deg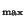 gives the maximal degree
occurring during the GB computation w.r.t. the degree reverse
lexicographical ordering. The last column gives references to, our
sources of these examples
gives the maximal degree
occurring during the GB computation w.r.t. the degree reverse
lexicographical ordering. The last column gives references to, our
sources of these examples![[*]](http://www.mathematik.uni-kl.de/%7Ezca/icons.gif/foot_motif.gif) . Those without
a reference are from the collection of examples of the
SINGULAR team.
. Those without
a reference are from the collection of examples of the
SINGULAR team.
Finally, in the rest of this appendix, we completely list the all the
used examples.
- cyclic n:
-
![$[x_1, \ldots x_n]$](img55.gif) ,
n generators pk:
,
n generators pk:
For example, cyclic 4:
- homog cyclic n:
-
![$[x_1, \ldots x_{n+1}]$](img58.gif) ,
n generators pk:
,
n generators pk:
For example, homog cyclic 4:
- rcyclic n:
-
![$[x_1, \ldots x_n]$](img55.gif) ,
n generators pk:
,
n generators pk:
For example, rcyclic 4:
- ecyclic n:
-
![$[x_1, \ldots x_{n(n-1) + 1}]$](img63.gif) ,
n generators pk:
,
n generators pk:
For example, ecyclic 4:
[ht]



Next: Appendix B: Timings on
Up: Monomial Representations for Gröbner Computations
Previous: Bibliography
| ZCA Home |
Reports |
![]() gives the maximal degree
occurring during the GB computation w.r.t. the degree reverse
lexicographical ordering. The last column gives references to, our
sources of these examples
gives the maximal degree
occurring during the GB computation w.r.t. the degree reverse
lexicographical ordering. The last column gives references to, our
sources of these examples![]() . Those without
a reference are from the collection of examples of the
SINGULAR team.
. Those without
a reference are from the collection of examples of the
SINGULAR team.