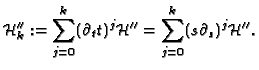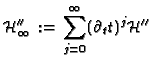Next: Computation
Up: Algorithm
Previous: Algorithm
Since
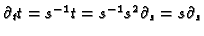 , the
, the
are
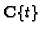 -lattices and
-lattices and
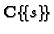 -lattices.
Since
-lattices.
Since
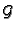 is regular, the saturation
of
is regular, the saturation
of
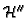 is a
is a
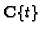 -lattice and, hence,
-lattice and, hence,
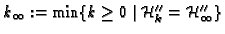 is a finite number.
For any
is a finite number.
For any 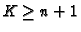 the inclusions
the inclusions
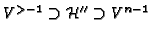 imply inclusions
and
imply inclusions
and
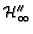 and
and
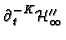 are
are
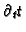 -invariant. Hence,
-invariant. Hence,
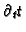 and
and
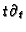 induce endomorphisms
induce endomorphisms
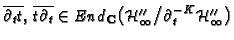 such that the V-filtration
such that the V-filtration
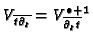 defined by
defined by
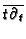 on
on
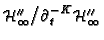 induces the V-filtration on the subquotient
induces the V-filtration on the subquotient
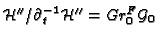 .
.
Christoph Lossen
2001-03-21
![]() , the
, the