|
|
7.4.3 Syzygies and resolutions (plural)
Syzygies
Let 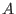 be a GR-algebra. A left (resp. right) syzygy
between be a GR-algebra. A left (resp. right) syzygy
between 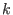 elements elements
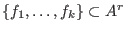 is
a is
a 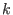 -tuple -tuple
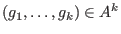 satisfying satisfying
The set of all left (resp. right) syzygies between
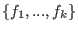 is a left (resp. right) submodule is a left (resp. right) submodule 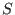 of of 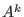 . .
Remark:
With respect to the definitions of ideal and module (see PLURAL), PLURAL works with left
syzygies only (by syz we understand a left syzygy).
If S is a matrix of a left syzygy module of left submodule given by matrix M, then transpose(S)*transpose(M) = 0
(but, in general,
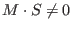 ). ).
Note, that the syzygy modules of
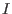 depend on a choice of generators depend on a choice of generators
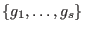 , but one can show that they depend on , but one can show that they depend on
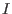 uniquely up to direct summands. uniquely up to direct summands.
Free resolutions
Let
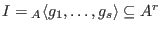 and and 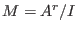 .
A free resolution of .
A free resolution of 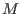 is a long exact sequence is a long exact sequence
with
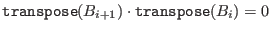
and where the columns of the matrix
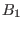 generate generate
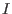 . Note, that resolutions over factor-algebras need not to be of finite length. . Note, that resolutions over factor-algebras need not to be of finite length.
Generalized Hilbert Syzygy Theorem
For a 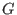 -algebra -algebra 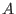 , generated by , generated by 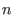 variables, there exists a free resolution of length smaller or equal than variables, there exists a free resolution of length smaller or equal than
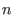 . .
Example:
| | ring R=0,(x,y,z),dp;
matrix d[3][3];
d[1,2]=-z; d[1,3]=2x; d[2,3]=-2y;
def U=nc_algebra(1,d); // this algebra is U(sl_2)
setring U;
option(redSB); option(redTail);
ideal I=x3,y3,z3-z;
I=std(I);
I;
==> I[1]=z3-z
==> I[2]=y3
==> I[3]=x3
==> I[4]=y2z2-y2z
==> I[5]=x2z2+x2z
==> I[6]=x2y2z-2xyz2-2xyz+2z2+2z
resolution resI = mres(I,0);
resI;
==> 1 5 7 3
==> U <-- U <-- U <-- U
==>
==> 0 1 2 3
==>
list l = resI;
// The matrix A_1 is given by
print(matrix(l[1]));
==> z3-z,y3,x3,y2z2-y2z,x2z2+x2z
// We see that the columns of A_1 generate I.
// The matrix A_2 is given by
print(matrix(l[2]));
==> 0, 0, y2, x2, 6yz, -36xy+18z+24,-6xz,
==> z2+11z+30,0, 0, 0, 2x2z+12x2, 2x3, 0,
==> 0, z2-11z+30,0, 0, 0, -2y3, 2y2z-12y2,
==> -y, 0, -z-5,0, x2y-6xz-30x,9x2, x3,
==> 0, -x, 0, -z+5,-y3, -9y2, -xy2-4yz+28y
ideal tst; // now let us show that the resolution is exact
matrix TST;
TST = transpose(l[3])*transpose(l[2]); // 2nd term
size(ideal(TST));
==> 0
TST = transpose(l[2])*transpose(l[1]); // 1st term
size(ideal(TST));
==> 0
|
|
 Online Manual
Online Manual