7.4.2 Groebner bases in G-algebras
We follow the notations, used in the SINGULAR Manual (e.g. in Standard bases).
For a 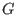 -algebra -algebra 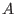 , we denote by , we denote by
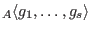 the left submodule of a free module
the left submodule of a free module 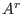 , generated by elements , generated by elements
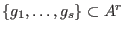 . .
Let 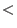 be a fixed monomial well-ordering on the be a fixed monomial well-ordering on the 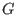 -algebra -algebra 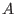 with the Poincar@'e-Birkhoff-Witt (PBW) basis with the Poincar@'e-Birkhoff-Witt (PBW) basis
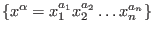 .
For a given free module .
For a given free module 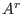 with the basis with the basis
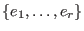 , , 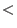 denotes also a
fixed module ordering on the set of monomials denotes also a
fixed module ordering on the set of monomials
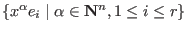 . .
Definition
For a set 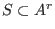 , define , define
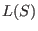 to be the to be the 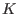 -vector space, spanned on the leading monomials
of elements of -vector space, spanned on the leading monomials
of elements of 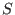 , ,
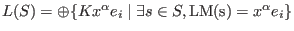 . .
We call 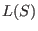 the span of leading monomials of the span of leading monomials of 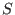 . .
Let 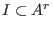 be a left be a left 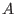 -submodule.
A finite set -submodule.
A finite set 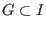 is called a left Groebner basis of is called a left Groebner basis of 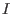 if and
only if if and
only if 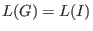 , that is for any , that is for any
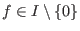 there exists a there exists a 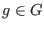 satisfying
satisfying
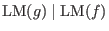 , i.e., if , i.e., if
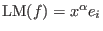 , then , then
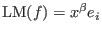 with with
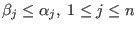 . .
Remark: In general non-commutative algorithms are working with global well-orderings
only (see PLURAL, Monomial orderings and Term orderings), unless we deal with
graded commutative algebras via Graded commutative algebras (SCA).
A Groebner basis 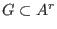 is called minimal (or reduced) if is called minimal (or reduced) if 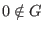 and if and if
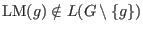 for all for all 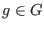 .
Note, that any Groebner basis can be made minimal by deleting successively those .
Note, that any Groebner basis can be made minimal by deleting successively those
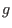 with with
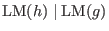 for some for some
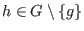 . .
For 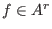 and and 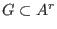 we say that we say that 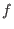 is completely reduced with
respect to is completely reduced with
respect to 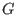 if no monomial of if no monomial of 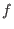 is contained in is contained in 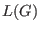 . .
Left Normal Form
A map
 , is called a (left) normal form
on , is called a (left) normal form
on 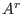 if for any if for any 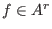 and any left Groebner basis and any left Groebner basis 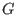 the following
holds: the following
holds:
(i)
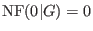 , ,
(ii) if
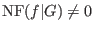 then then 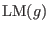 does not divide does not divide
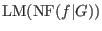 for all for all 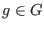 , ,
(iii)
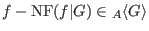 . .
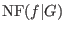 is called a left normal form of is called a left normal form of 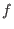 with
respect to with
respect to 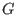 (note that such a map is not unique). (note that such a map is not unique).
Remark:
As we have already mentioned in the definitions ideal and module (see
PLURAL), by NF (or reduce) PLURAL understands a left normal form.
Note, that rightNF from nctools_lib allows to compute a right normal form.
Left ideal membership (plural)
For a left Groebner basis 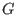 of of 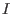 the following holds: the following holds:
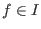 if and only if the left normal form if and only if the left normal form
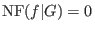 . .
For computing a left Groebner basis G of I, use std (plural).
For computing a left normal form of f with respect to G, use reduce (plural).
Right ideal membership (plural)
The right ideal membership is analogous to the left one:
for computing a right Groebner basis G of I, use rightStd from nctools_lib,
for computing a right normal form of f with respect to G, use rightNF from nctools_lib.
Two-sided ideal membership (plural)
Let 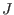 be a two-sided ideal and be a two-sided ideal and 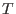 be a two-sided Groebner basis of be a two-sided Groebner basis of 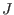 . .
Then 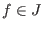 if and only if the left normal form if and only if the left normal form
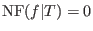 . .
For computing a two-sided Groebner basis T of J, use twostd (plural),
for computing a normal form of f with respect to T, use reduce (plural).
|
 Online Manual
Online Manual