Singular

7.3.19 oppose

Syntax:

oppose ( ring_name, name )

Type:

poly, vector, ideal, module or matrix (the same type as the second argument)

Purpose:

for a given object in the given ring, creates its opposite object in the opposite ( opposite) ring (the last one is assumed to be the current ring).

Remark:

for any object .

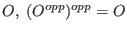LIB "ncalg.lib"; def R = makeUsl2(); setring R; matrix m[3][4]; poly p = (h^2-1)*f*e; vector v = [1,e*h,0,p]; ideal i = h*e, f^2*e,h*f*e; m = e,f,h,1,0,h^2, p,0,0,1,e^2,e*f*h+1; module mm = module(m); def b = opposite(R); setring b; b; ==> // coefficients: QQ ==> // number of vars : 3 ==> // block 1 : ordering a ==> // : names H F E ==> // : weights 1 1 1 ==> // block 2 : ordering ls ==> // : names H F E ==> // block 3 : ordering C ==> // noncommutative relations: ==> // FH=HF-2F ==> // EH=HE+2E ==> // EF=FE-H // we will oppose these objects: p,v,i,m,mm poly P = oppose(R,p); vector V = oppose(R,v); ideal I = oppose(R,i); matrix M = oppose(R,m); module MM = oppose(R,mm); def c = opposite(b); setring c; // now let's check the correctness: // print compact presentations of objects print(oppose(b,P)-imap(R,p)); ==> 0 print(oppose(b,V)-imap(R,v)); ==> [0] print(matrix(oppose(b,I))-imap(R,i)); ==> 0,0,0 print(matrix(oppose(b,M))-imap(R,m)); ==> 0,0,0,0, ==> 0,0,0,0, ==> 0,0,0,0 print(matrix(oppose(b,MM))-imap(R,mm)); ==> 0,0,0,0, ==> 0,0,0,0, ==> 0,0,0,0