|
|
7.3.20 opposite
Syntax:
opposite ( ring_name )
Type:
- ring
Purpose:
- creates an opposite algebra of a given algebra.
Note:
- activate the ring with the
setring command.
An opposite algebra of a given algebra (
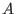 ,#) is
an algebra ( ,#) is
an algebra (
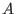 ,*) with the same vector space but with the opposite
multiplication, i.e. ,*) with the same vector space but with the opposite
multiplication, i.e.
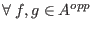 , a new multiplication , a new multiplication 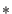 on on 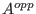 is defined to be
is defined to be
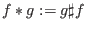 . .
This is an identity functor on commutative algebras.
Remark:
- Starting from the variables x_1,...,x_N and the ordering
<
of the given algebra,
an opposite algebra will have variables X_N,...,X_1
(where the case and the position are reverted). Moreover, it is
equipped with an opposed ordering <_opp (it is given
by the matrix, obtained from the matrix ordering of <
with the reverse order of columns).
Currently not implemented for non-global orderings.
| | LIB "ncalg.lib";
def B = makeQso3(3);
// this algebra is a quantum deformation of U(so_3),
// where the quantum parameter is a 6th root of unity
setring B; B;
==> // coefficients: QQ[Q]/(Q2-Q+1)
==> // number of vars : 3
==> // block 1 : ordering dp
==> // : names x y z
==> // block 2 : ordering C
==> // noncommutative relations:
==> // yx=(Q-1)*xy+(-Q)*z
==> // zx=(-Q)*xz+(-Q+1)*y
==> // zy=(Q-1)*yz+(-Q)*x
def Bopp = opposite(B);
setring Bopp;
Bopp;
==> // coefficients: QQ[Q]/(Q2-Q+1)
==> // number of vars : 3
==> // block 1 : ordering a
==> // : names Z Y X
==> // : weights 1 1 1
==> // block 2 : ordering ls
==> // : names Z Y X
==> // block 3 : ordering C
==> // noncommutative relations:
==> // YZ=(Q-1)*ZY+(-Q)*X
==> // XZ=(-Q)*ZX+(-Q+1)*Y
==> // XY=(Q-1)*YX+(-Q)*Z
def Bcheck = opposite(Bopp);
setring Bcheck; Bcheck; // check that (B-opp)-opp = B
==> // coefficients: QQ[Q]/(Q2-Q+1)
==> // number of vars : 3
==> // block 1 : ordering wp
==> // : names x y z
==> // : weights 1 1 1
==> // block 2 : ordering C
==> // block 3 : ordering C
==> // noncommutative relations:
==> // yx=(Q-1)*xy+(-Q)*z
==> // zx=(-Q)*xz+(-Q+1)*y
==> // zy=(Q-1)*yz+(-Q)*x
|
See
Matrix orderings;
envelope;
oppose.
|