
C is given by the 2x2-minors of the matrix:
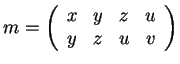 |
|
|
|
versal(f0);
|

|
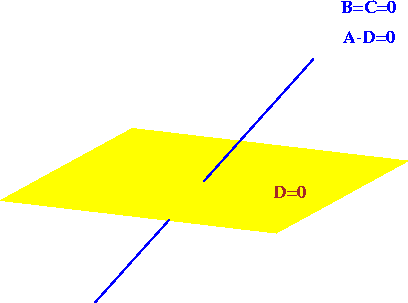
Versal Deformation - Base Space
|
|||||||||||
|
|
||||||||||||
| Sao Carlos, 08/02 | http://www.singular.uni-kl.de | |||||||||||