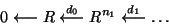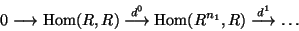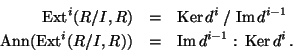|
Equidimensional Part
Task: Calculate the equidimensional part
of a variety via Ext-groups.
Based on a free resolution of R/I,
and its dual,
we get
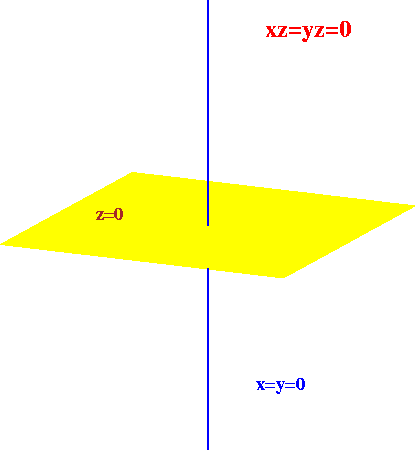
In particular, the equidimensional part of V={xz=yz=0} is
given by the ideal:
This can be computed with
SINGULAR
using the following
commands:
ring r = 0,(x,y,z),dp;
ideal I = xz,yz;
int i = 1;
resolution L = res(I, i+1);
module Im = transpose(L[i]);
module Ker = syz(transpose(L[i+1]));
module Ext = modulo(Ker,Im);
ideal Ann = quotient(Im,Ker);
Ann;
Another possibility is to use the library
homolog.lib:
LIB "homolog.lib";
module m=Ext_R(1,I);
quotient(m,freemodule(nrows(m)));
|
|
|