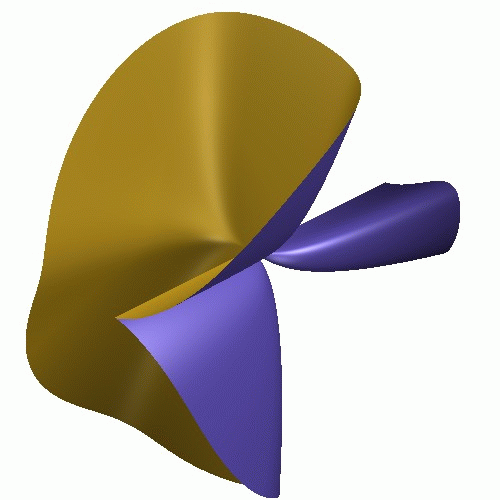|
Non-Normal Locus
| Theorem:
|
Let R be a reduced
Noetherian ring, J an ideal in R and let a be
any element of J which is a non-zerodivisor for R. Then
the non-normal locus of R is given by
AnnR ( HomR(J,J) / R )
= <a> : (aJ:J) .
|
We compute the non-normal locus of the ring R :=
Q[x,y,z] / <
xy2-xz3-z6 > :
LIB"primdec.lib";
ring A = 0,(x,y,z),dp;
ideal I = xy2-xz3-z6;
ideal sing = I+jacob(I);
ideal J = radical(sing);
qring R = std(I); // quotient ring A/I
ideal J = fetch(A,J);
ideal a = J[1]; // a non-zero element of J
quotient(a,quotient(a*J,J)); // <a>:(aJ:J)
|
|
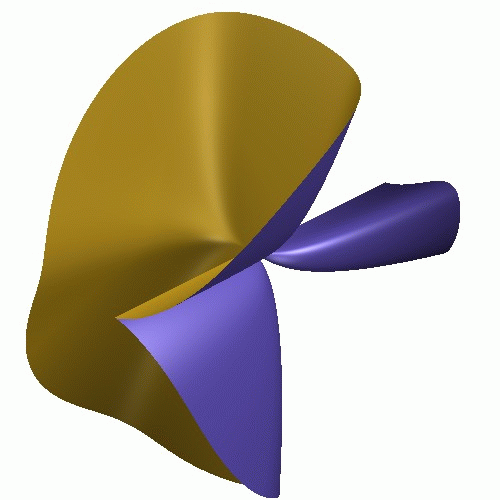
|
From the output, we read that the non-normal locus is the x-axis (the
zero-set of <y,z>).
|