Task: Compute a matrix M such that
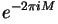is a monodromy matrix of the singularity f.
ring R=0,(x,y),ds; poly f=x5+y5+x2y2; // A'Campo example
To compute the Jordan data of M, we can use:
LIB "gaussman.lib";
monodromy(f);
==> |
[1]: // the eigenvalues of M
_[1]=1/2 _[2]=7/10 _[3]=9/10 _[4]=1 _[5]=11/10 _[6]=13/10
[2]: // the Block sizes
2,1,1,1,1,1
[3]: // the multiplicities
1,2,2,1,2,2
|
LIB "mondromy.lib"; LIB "linalg.lib"; matrix M = monodromyB(f); // using Brieskorn algorithm print(jordannf(M));