Das Cycloheptane Molekül: c = 1/3
Gleichungen für den Konfigurationsraum des Moleküls (in Singular):
ring rs=0,(v,w,x,y,z,t),dp; ideal i= 81y2z2-54wyz+54y2z+54yz2-72w2+198wy-207y2+198wz-225yz-207z2+114w-141y-141z+10, 81w2x2+54w2x+54wx2-54wxz-207w2-225wx-207x2+198wz+198xz-72z2-141w-141x+114z+10, 324vw2x+432vw2+540vwx+432w2x-432wxy-432vwz+324wyz+180vw+846w2-576vx+180wx-306wy +144xy+144vz-306wz-36yz+12v+585w+12x-318y-318z-79, 81v2w2+54v2w+54vw2-54vwy-207v2-225vw-207w2+198vy+198wy-72y2-141v-141w+114y+10;
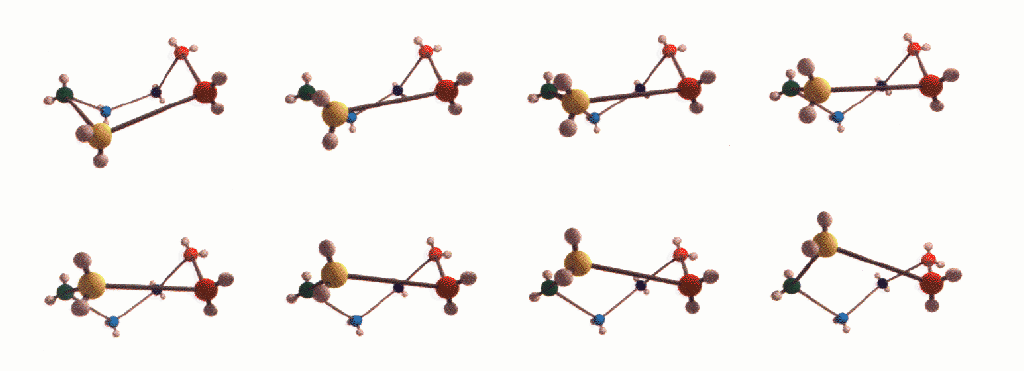Die Gleichungen beschreiben eine Kurve im
R5. Die Projektion ouf die w,x - Ebene
erhät man wie folgt:
ideal j=homog(i,t); intvec hi=1,0,0,0,-4,0,0,0,6,2,-3,0,-3,-2,3,0; ideal k3=eliminate(j,vyz,hi); k3=subst(k3,t,1); size(k3[1]); //->357 K3; // Gleichung der Projektion auf die w.x - Ebene plot(K3[1]); // Bild der Kurve K3=0 in der w,x - Ebene