|
|
7.6.1 Free associative algebras
Let
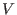 be a be a
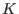 -vector space, spanned by the symbols -vector space, spanned by the symbols
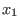 ,..., ,...,
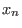 .
A free associative algebra in .
A free associative algebra in
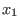 ,..., ,...,
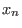 over over
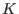 , denoted by , denoted by
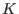 < <
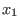 ,..., ,...,
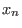 >
is also known as a tensor algebra >
is also known as a tensor algebra
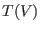 of of
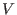 . It is an infinite dimensional . It is an infinite dimensional
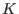 -vector space, where one can take
as a basis the elements of the free monoid < -vector space, where one can take
as a basis the elements of the free monoid <
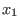 ,..., ,...,
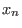 >, identifying the identity element (the empty word) with the >, identifying the identity element (the empty word) with the
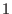 in in
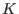 . In other
words, the monomials of . In other
words, the monomials of
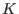 < <
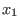 ,..., ,...,
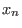 > are the words
of finite length in the finite alphabet { > are the words
of finite length in the finite alphabet {
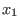 ,..., ,...,
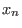 }. The algebra }. The algebra
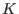 < <
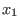 ,..., ,...,
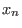 > is an
integral domain, which is not Noetherian for > is an
integral domain, which is not Noetherian for
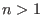 (hence, a two-sided Groebner basis of a finitely generated ideal might be infinite). The free associative algebra can be regarded as a graded algebra in a natural way. (hence, a two-sided Groebner basis of a finitely generated ideal might be infinite). The free associative algebra can be regarded as a graded algebra in a natural way.
Any finitely presented associative algebra is isomorphic to a
quotient of
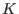 < <
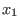 ,..., ,...,
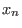 > modulo a two-sided ideal. > modulo a two-sided ideal.
|