cf_map_ext.h File Reference

This file implements functions to map between extensions of finite fields. More...

Go to the source code of this file.

Functions
int	findItem (const CFList &list, const CanonicalForm &item)
	helper function More...
CanonicalForm	getItem (const CFList &list, const int &pos)
	helper function More...
CanonicalForm	GFMapUp (const CanonicalForm &F, int k)
	maps a polynomial over to a polynomial over , d needs to be a multiple of k More...
CanonicalForm	GFMapDown (const CanonicalForm &F, int k)
	maps a polynomial over to a polynomial over , d needs to be a multiple of k More...
CanonicalForm	mapUp (const CanonicalForm &F, const Variable &alpha, const Variable &beta, const CanonicalForm &prim_elem, const CanonicalForm &im_prim_elem, CFList &source, CFList &dest)
	map F from to . We assume . More...
CanonicalForm	mapDown (const CanonicalForm &F, const CanonicalForm &prim_elem, const CanonicalForm &im_prim_elem, const Variable &alpha, CFList &source, CFList &dest)
	map F from to . We assume and F in . More...
CanonicalForm	primitiveElement (const Variable &alpha, Variable &beta, bool &fail)
	determine a primitive element of , is a primitive element of a field which is isomorphic to More...
CanonicalForm	mapPrimElem (const CanonicalForm &prim_elem, const Variable &alpha, const Variable &beta)
	compute the image of a primitive element of in . We assume . More...
CanonicalForm	GF2FalphaRep (const CanonicalForm &F, const Variable &alpha)
	changes representation by primitive element to representation by residue classes modulo a Conway polynomial More...
CanonicalForm	Falpha2GFRep (const CanonicalForm &F)
	change representation by residue classes modulo a Conway polynomial to representation by primitive element More...
CanonicalForm	map (const CanonicalForm &primElem, const Variable &alpha, const CanonicalForm &F, const Variable &beta)
	map from to such that is mapped onto More...
CanonicalForm	findMinPoly (const CanonicalForm &F, const Variable &alpha)
	compute minimal polynomial of via NTL More...

Detailed Description

This file implements functions to map between extensions of finite fields.

Copyright:

(c) by The SINGULAR Team, see LICENSE file

Author

Martin Lee

Date

16.11.2009

Definition in file cf_map_ext.h.

Function Documentation

Falpha2GFRep()

CanonicalForm Falpha2GFRep

(

const CanonicalForm &

F

)

change representation by residue classes modulo a Conway polynomial to representation by primitive element

Parameters

[in]

F

some poly over F_p(alpha) where alpha is a root of a Conway poly

Definition at line 203 of file cf_map_ext.cc.

{
  CanonicalForm result= 0;
  InternalCF* buf;
 
  if (F.inCoeffDomain())
  {
    if (F.inBaseDomain())
      return F.mapinto();
    else
    {
      for (CFIterator i= F; i.hasTerms(); i++)
      {
        buf= int2imm_gf (i.exp());
        result += i.coeff().mapinto()*CanonicalForm (buf);
      }
    }
    return result;
  }
  for (CFIterator i= F; i.hasTerms(); i++)
    result += Falpha2GFRep (i.coeff())*power (F.mvar(), i.exp());
  return result;
}

findItem()

int findItem	(	const CFList &	list,
		const CanonicalForm &	item
	)

helper function

Definition at line 41 of file cf_map_ext.cc.

{
  int result= 1;
  for (CFListIterator i= list; i.hasItem(); i++, result++)
  {
    if (i.getItem() == item)
      return result;
  }
  return 0;
}

findMinPoly()

CanonicalForm findMinPoly	(	const CanonicalForm &	F,
		const Variable &	alpha
	)

compute minimal polynomial of 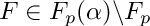via NTL

Returns

findMinPoly computes the minimal polynomial of F

Parameters

[in]	F	an element of
[in]	alpha	algebraic variable

Definition at line 640 of file cf_map_ext.cc.

{
  ASSERT (F.isUnivariate() && F.mvar()==alpha,"expected element of F_p(alpha)");
 
  int p=getCharacteristic();
  #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20503)
  nmod_poly_t FLINT_F,FLINT_alpha,g;
  nmod_poly_init(g,p);
  convertFacCF2nmod_poly_t(FLINT_F,F);
  convertFacCF2nmod_poly_t(FLINT_alpha,getMipo(alpha));
  minpoly(g,FLINT_F,FLINT_alpha);
  nmod_poly_clear(FLINT_alpha);
  nmod_poly_clear(FLINT_F);
  CanonicalForm res=convertnmod_poly_t2FacCF(g,Variable(1));
  nmod_poly_clear(g);
  return res;
  #elif defined(HAVE_NTL)
  if (fac_NTL_char != p)
  {
    fac_NTL_char= p;
    zz_p::init (p);
  }
  zz_pX NTLF= convertFacCF2NTLzzpX (F);
  int d= degree (getMipo (alpha));
 
  zz_pX NTLMipo= convertFacCF2NTLzzpX (getMipo(alpha));
  zz_pE::init (NTLMipo);
  vec_zz_p pows;
  pows.SetLength (2*d);
 
  zz_pE powNTLF;
  set (powNTLF);
  zz_pE NTLFE= to_zz_pE (NTLF);
  zz_pX buf;
  for (int i= 0; i < 2*d; i++)
  {
    buf= rep (powNTLF);
    buf.rep.SetLength (d);
    pows [i]= buf.rep[0];
    powNTLF *= NTLFE;
  }
 
  zz_pX NTLMinPoly;
  MinPolySeq (NTLMinPoly, pows, d);
 
  return convertNTLzzpX2CF (NTLMinPoly, Variable (1));
  #else
  factoryError("NTL/FLINT missing: findMinPoly");
  #endif
}

getItem()

CanonicalForm getItem	(	const CFList &	list,
		const int &	pos
	)

helper function

Definition at line 53 of file cf_map_ext.cc.

{
  int j= 1;
  if ((pos > 0) && (pos <= list.length()))
  {
    for (CFListIterator i= list; j <= pos; i++, j++)
    {
      if (j == pos)
        return i.getItem();
    }
  }
  return 0;
}

GF2FalphaRep()

CanonicalForm GF2FalphaRep	(	const CanonicalForm &	F,
		const Variable &	alpha
	)

changes representation by primitive element to representation by residue classes modulo a Conway polynomial

Parameters

[in]	F	some poly over GF
[in]	alpha	root of a Conway poly

Definition at line 195 of file cf_map_ext.cc.

{
  Variable beta= rootOf (gf_mipo);
  CanonicalForm result= GF2FalphaHelper (F, beta) (alpha, beta);
  prune (beta);
  return result;
}

GFMapDown()

CanonicalForm GFMapDown	(	const CanonicalForm &	F,
		int	k
	)

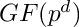
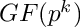
maps a polynomial over to a polynomial over , d needs to be a multiple of k

Definition at line 276 of file cf_map_ext.cc.

{
  int d= getGFDegree();
  ASSERT (d % k == 0, "multiple of GF degree expected");
  int p= getCharacteristic();
  int ext_field_size= ipower (p, d);
  int field_size= ipower ( p, k);
  int diff= (ext_field_size - 1)/(field_size - 1);
  return GFPowDown (F, diff);
}

GFMapUp()

CanonicalForm GFMapUp	(	const CanonicalForm &	F,
		int	k
	)

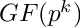
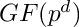
maps a polynomial over to a polynomial over , d needs to be a multiple of k

Definition at line 240 of file cf_map_ext.cc.

{
  int d= getGFDegree();
  ASSERT (d%k == 0, "multiple of GF degree expected");
  int p= getCharacteristic();
  int ext_field_size= ipower (p, d);
  int field_size= ipower ( p, k);
  int diff= (ext_field_size - 1)/(field_size - 1);
  return GFPowUp (F, diff);
}

map()

CanonicalForm map	(	const CanonicalForm &	primElem,
		const Variable &	alpha,
		const CanonicalForm &	F,
		const Variable &	beta
	)

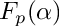
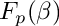
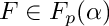
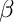
map from to such that is mapped onto

Returns

map returns the image of primElem such that the above described properties hold

Parameters

[in]	primElem	primitive element of
[in]	alpha	algebraic variable
[in]	F	an element of , whose minimal polynomial defines a field extension of of degree
[in]	beta	algebraic variable, root of F's minimal polynomial

Definition at line 504 of file cf_map_ext.cc.

{
  CanonicalForm G= F;
  int order= 0;
  while (!G.isOne())
  {
    G /= primElem;
    order++;
  }
  #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20503)
  // convert mipo
  nmod_poly_t mipo1;
  convertFacCF2nmod_poly_t(mipo1,getMipo(beta));
  fq_nmod_ctx_t ctx;
  fq_nmod_ctx_init_modulus(ctx,mipo1,"t");
  nmod_poly_clear(mipo1);
  // convert mipo2 (alpha)
  fq_nmod_poly_t mipo2;
  convertFacCF2Fq_nmod_poly_t(mipo2,getMipo(alpha),ctx);
  fq_nmod_poly_factor_t fac;
  fq_nmod_poly_factor_init(fac,ctx);
  fq_nmod_poly_roots(fac, mipo2, 0, ctx);
  // roots in fac, #=fac->num
  int ind=-1;
  fq_nmod_t r0,FLINTbeta;
  fq_nmod_init(r0, ctx);
  fq_nmod_init(FLINTbeta, ctx);
  convertFacCF2Fq_nmod_t(FLINTbeta,beta,ctx);
  fmpz_t FLINTorder;
  fmpz_set_si(FLINTorder,order);
  for(int i=0;i< fac->num;i++)
  {
    // get the root (-abs.term of linear factor)
    fq_nmod_poly_get_coeff(r0,fac->poly+i,0,ctx);
    fq_nmod_neg(r0,r0,ctx);
    // r^order
    fq_nmod_pow(r0,r0,FLINTorder,ctx);
    // ==beta?
    if (fq_nmod_equal(r0,FLINTbeta,ctx))
    {
       ind=i;
       break;
    }
  }
  fmpz_clear(FLINTorder);
  // convert
  fq_nmod_poly_get_coeff(r0,fac->poly+ind,0,ctx);
  fq_nmod_neg(r0,r0,ctx);
  CanonicalForm r1=convertFq_nmod_t2FacCF(r0,beta,ctx);
  // cleanup
  fq_nmod_poly_factor_clear(fac,ctx);
  fq_nmod_clear(r0, ctx);
  fq_nmod_clear(FLINTbeta,ctx);
  fq_nmod_poly_clear(mipo2,ctx);
  fq_nmod_ctx_clear(ctx);
  return r1;
  #elif defined(HAVE_NTL)
  int p= getCharacteristic ();
  if (fac_NTL_char != p)
  {
    fac_NTL_char= p;
    zz_p::init (p);
  }
  zz_pX NTL_mipo= convertFacCF2NTLzzpX (getMipo (beta));
  zz_pE::init (NTL_mipo);
  zz_pEX NTL_alpha_mipo= convertFacCF2NTLzz_pEX (getMipo(alpha), NTL_mipo);
  zz_pE NTLBeta= to_zz_pE (convertFacCF2NTLzzpX (beta));
  vec_zz_pE roots= FindRoots (NTL_alpha_mipo);
  long ind=-1;
  for (long i= 0; i < roots.length(); i++)
  {
    if (power (roots [i], order)== NTLBeta)
    {
      ind= i;
      break;
    }
  }
  return (convertNTLzzpE2CF (roots[ind], beta));
  #else
  factoryError("NTL/FLINT missing: map");
  return CanonicalForm(0);
  #endif
}

mapDown()

CanonicalForm mapDown	(	const CanonicalForm &	F,
		const CanonicalForm &	prim_elem,
		const CanonicalForm &	im_prim_elem,
		const Variable &	alpha,
		CFList &	source,
		CFList &	dest
	)

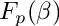
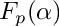
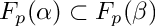
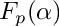
map F from to . We assume and F in .

Parameters

[in]	F	poly over
[in]	prim_elem	primitive element of
[in]	im_prim_elem	image of prim_elem in
[in]	alpha	alg. variable
[in,out]	source	look up lists
[in,out]	dest	look up lists

Definition at line 431 of file cf_map_ext.cc.

{
  return mapUp (F, im_prim_elem, alpha, prim_elem, dest, source);
}

mapPrimElem()

CanonicalForm mapPrimElem	(	const CanonicalForm &	prim_elem,
		const Variable &	alpha,
		const Variable &	beta
	)

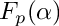
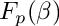
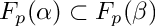
compute the image of a primitive element of in . We assume .

Parameters

[in]	prim_elem	primitive element
[in]	alpha	algebraic variable
[in]	beta	algebraic variable

Definition at line 450 of file cf_map_ext.cc.

{
  if (primElem == alpha)
    return mapUp (alpha, beta);
  else
  {
    CanonicalForm primElemMipo= findMinPoly (primElem, alpha);
    #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20503)
    // convert mipo1
    nmod_poly_t mipo1;
    convertFacCF2nmod_poly_t(mipo1,getMipo(beta));
    fq_nmod_ctx_t ctx;
    fq_nmod_ctx_init_modulus(ctx,mipo1,"t");
    nmod_poly_clear(mipo1);
    // convert mipo2 (primElemMipo)
    fq_nmod_poly_t mipo2;
    convertFacCF2Fq_nmod_poly_t(mipo2,primElemMipo,ctx);
    fq_nmod_poly_factor_t fac;
    fq_nmod_poly_factor_init(fac,ctx);
    fq_nmod_poly_roots(fac, mipo2, 0, ctx);
    // root of first (linear) factor: -absolute Term
    fq_nmod_t r0;
    fq_nmod_init(r0, ctx);
    fq_nmod_poly_get_coeff(r0,fac->poly,0,ctx);
    fq_nmod_neg(r0, r0, ctx);
    // convert
    CanonicalForm r1=convertFq_nmod_t2FacCF(r0,beta,ctx);
    // cleanup
    fq_nmod_poly_factor_clear(fac,ctx);
    fq_nmod_clear(r0, ctx);
    fq_nmod_poly_clear(mipo2,ctx);
    fq_nmod_ctx_clear(ctx);
    return r1;
    #elif defined(HAVE_NTL)
    int p= getCharacteristic ();
    if (fac_NTL_char != p)
    {
      fac_NTL_char= p;
      zz_p::init (p);
    }
    zz_pX NTLMipo= convertFacCF2NTLzzpX (getMipo (beta));
    zz_pE::init (NTLMipo);
    zz_pEX NTLPrimElemMipo= convertFacCF2NTLzz_pEX (primElemMipo, NTLMipo);
    zz_pE root= FindRoot (NTLPrimElemMipo);
    return convertNTLzzpE2CF (root, beta);
    #else
    factoryError("NTL/FLINT missing: mapPrimElem");
    #endif
  }
}

mapUp()

CanonicalForm mapUp	(	const CanonicalForm &	F,
		const Variable &	alpha,
		const Variable &	beta,
		const CanonicalForm &	prim_elem,
		const CanonicalForm &	im_prim_elem,
		CFList &	source,
		CFList &	dest
	)

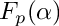
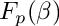
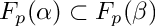
map F from to . We assume .

Parameters

[in]	F	poly over
[in]	alpha	alg. variable
[in]	beta	alg. variable
[in]	prim_elem	primitive element of
[in]	im_prim_elem	image of prim_elem in
[in,out]	source	look up lists
[in,out]	dest	look up lists

Definition at line 439 of file cf_map_ext.cc.

{
  if (prim_elem == alpha)
    return F (im_prim_elem, alpha);
  return mapUp (F, prim_elem, alpha, im_prim_elem, source, dest);
}

primitiveElement()

CanonicalForm primitiveElement	(	const Variable &	alpha,
		Variable &	beta,
		bool &	fail
	)

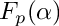
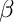
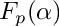
determine a primitive element of , is a primitive element of a field which is isomorphic to

Parameters

[in]	alpha	some algebraic variable
[in,out]	beta	s.a.
[in,out]	fail	failure due to integer factorization failure?

Definition at line 342 of file cf_map_ext.cc.

{
  bool primitive= false;
  fail= false;
  primitive= isPrimitive (alpha, fail);
  if (fail)
    return 0;
  if (primitive)
  {
    beta= alpha;
    return alpha;
  }
  CanonicalForm mipo= getMipo (alpha);
  int d= degree (mipo);
  int p= getCharacteristic ();
  #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20503)
  nmod_poly_t FLINT_mipo;
  nmod_poly_init(FLINT_mipo,p);
  #elif defined(HAVE_NTL)
  if (fac_NTL_char != p)
  {
    fac_NTL_char= p;
    zz_p::init (p);
  }
  zz_pX NTL_mipo;
  #else
  factoryError("NTL/FLINT missing: primitiveElement");
  return CanonicalForm(0);
  #endif
  CanonicalForm mipo2;
  primitive= false;
  fail= false;
  bool initialized= false;
  do
  {
    #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20503)
    nmod_poly_randtest_monic_irreducible(FLINT_mipo, FLINTrandom, d+1);
    mipo2=convertnmod_poly_t2FacCF(FLINT_mipo,Variable(1));
    #elif defined(HAVE_NTL)
    BuildIrred (NTL_mipo, d);
    mipo2= convertNTLzzpX2CF (NTL_mipo, Variable (1));
    #endif
    if (!initialized)
      beta= rootOf (mipo2);
    else
      setMipo (beta, mipo2);
    primitive= isPrimitive (beta, fail);
    if (primitive)
      break;
    if (fail)
      return 0;
  } while (1);
  #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20503)
  nmod_poly_clear(FLINT_mipo);
  // convert alpha_mipo
  nmod_poly_t alpha_mipo;
  convertFacCF2nmod_poly_t(alpha_mipo,mipo);
  fq_nmod_ctx_t ctx;
  fq_nmod_ctx_init_modulus(ctx,alpha_mipo,"t");
  nmod_poly_clear(alpha_mipo);
  // convert beta_mipo (mipo2)
  fq_nmod_poly_t FLINT_beta_mipo;
  convertFacCF2Fq_nmod_poly_t(FLINT_beta_mipo,mipo2,ctx);
  fq_nmod_poly_factor_t fac;
  fq_nmod_poly_factor_init(fac,ctx);
  fq_nmod_poly_roots(fac, FLINT_beta_mipo, 0, ctx);
  // root of first (linear) factor: -absolute Term
  fq_nmod_t r0;
  fq_nmod_init(r0, ctx);
  fq_nmod_poly_get_coeff(r0,fac->poly,0,ctx);
  fq_nmod_neg(r0, r0, ctx);
  // convert
  CanonicalForm r1=convertFq_nmod_t2FacCF(r0,alpha,ctx);
  // cleanup
  fq_nmod_poly_factor_clear(fac,ctx);
  fq_nmod_clear(r0, ctx);
  fq_nmod_poly_clear(FLINT_beta_mipo,ctx);
  fq_nmod_ctx_clear(ctx);
  return r1;
  #elif defined(HAVE_NTL)
  zz_pX alpha_mipo= convertFacCF2NTLzzpX (mipo);
  zz_pE::init (alpha_mipo);
  zz_pEX NTL_beta_mipo= to_zz_pEX (NTL_mipo);
  zz_pE root= FindRoot (NTL_beta_mipo);
  return convertNTLzzpE2CF (root, alpha);
  #endif
}