
The ideal of a space curve singularity X is generated by the maximal minors of its presentation matrix M:
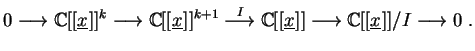
Any deformation of X is given by a perturbation of M.
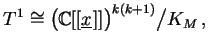
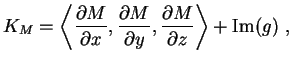
Stratification - An Example

|
Space Curve Singularities The ideal of a space curve singularity X is generated by the maximal minors of its presentation matrix M: 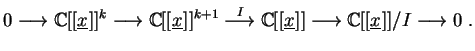
Any deformation of X is given by a perturbation of M. 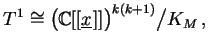
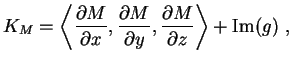
Stratification - An Example |
||||||||
|
|
|||||||||
| Sao Carlos, 08/02 | http://www.singular.uni-kl.de | ||||||||