 |
My Project
|
 |
My Project
|
This file provides functions for squarefrees factorizing over 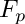
Go to the source code of this file.
Functions | |
| CFFList | squarefreeFactorization (const CanonicalForm &F, const Variable &alpha) |
| squarefree factorization over a finite field return a list of squarefree factors with multiplicity More... | |
| CFFList | FpSqrf (const CanonicalForm &F, bool sort=true) |
| squarefree factorization over | |
| CFFList | FqSqrf (const CanonicalForm &F, const Variable &alpha, bool sort=true) |
| squarefree factorization over | |
| CFFList | GFSqrf (const CanonicalForm &F, bool sort=true) |
| squarefree factorization over GF. If input is not monic, the leading coefficient is dropped More... | |
| CanonicalForm | sqrfPart (const CanonicalForm &F, CanonicalForm &pthPower, const Variable &alpha) |
| squarefree part of F/g, where g is the product of those squarefree factors whose multiplicity is 0 mod p, if F a pth power pthPower= F. More... | |
| CanonicalForm | maxpthRoot (const CanonicalForm &F, int q, int &l) |
| p^l-th root extraction, where l is maximal More... | |
This file provides functions for squarefrees factorizing over 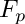
Definition in file facFqSquarefree.h.
|
inline |
squarefree factorization over 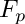
| [in] | F | a poly |
| [in] | sort | sort factors by exponent? |
Definition at line 38 of file facFqSquarefree.h.
|
inline |
squarefree factorization over 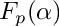
| [in] | F | a poly |
| [in] | alpha | algebraic variable |
| [in] | sort | sort factors by exponent? |
Definition at line 77 of file facFqSquarefree.h.
|
inline |
squarefree factorization over GF. If input is not monic, the leading coefficient is dropped
| [in] | F | a poly |
| [in] | sort | sort factors by exponent? |
Definition at line 116 of file facFqSquarefree.h.
| CanonicalForm maxpthRoot | ( | const CanonicalForm & | F, |
| int | q, | ||
| int & | l | ||
| ) |
p^l-th root extraction, where l is maximal
| [in] | F | a poly which is a pth power |
| [in] | q | size of the field |
| [in,out] | l | l maximal, s.t. F is a p^l-th power |
Definition at line 127 of file facFqSquarefree.cc.
| CanonicalForm sqrfPart | ( | const CanonicalForm & | F, |
| CanonicalForm & | pthPower, | ||
| const Variable & | alpha | ||
| ) |
squarefree part of F/g, where g is the product of those squarefree factors whose multiplicity is 0 mod p, if F a pth power pthPower= F.
| [in] | F | a poly |
| [in,out] | pthPower | returns F is F is a pthPower |
| [in] | alpha | algebraic variable |
Definition at line 303 of file facFqSquarefree.cc.
| CFFList squarefreeFactorization | ( | const CanonicalForm & | F, |
| const Variable & | alpha | ||
| ) |
squarefree factorization over a finite field return a list of squarefree factors with multiplicity
| [in] | F | a poly |
| [in] | alpha | either an algebraic variable, i.e. we are over some F_p (alpha) or a variable of level 1, i.e. we are F_p or GF |
Definition at line 181 of file facFqSquarefree.cc.