 |
My Project
|
 |
My Project
|
This file provides functions for factorizing a bivariate polynomial over 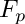
#include "config.h"#include "cf_assert.h"#include "cf_util.h"#include "debug.h"#include "timing.h"#include "canonicalform.h"#include "cf_defs.h"#include "cf_map_ext.h"#include "cf_random.h"#include "facHensel.h"#include "facMul.h"#include "cf_map.h"#include "cf_irred.h"#include "facFqBivarUtil.h"#include "facFqBivar.h"#include "cfNewtonPolygon.h"#include "NTLconvert.h"#include "FLINTconvert.h"Go to the source code of this file.
Functions | |
| TIMING_DEFINE_PRINT (fac_fq_uni_factorizer) TIMING_DEFINE_PRINT(fac_fq_bi_hensel_lift) TIMING_DEFINE_PRINT(fac_fq_bi_factor_recombination) TIMING_DEFINE_PRINT(fac_fq_bi_evaluation) TIMING_DEFINE_PRINT(fac_fq_bi_shift_to_zero) TIMING_DEFINE_PRINT(fac_fq_logarithmic) TIMING_DEFINE_PRINT(fac_fq_compute_lattice_lift) TIMING_DEFINE_PRINT(fac_fq_till_reduced) TIMING_DEFINE_PRINT(fac_fq_reconstruction) TIMING_DEFINE_PRINT(fac_fq_lift) TIMING_DEFINE_PRINT(fac_fq_uni_total) CanonicalForm prodMod0(const CFList &L | |
| else | if (L.length()==1) return mod(L.getFirst()(0 |
| else L | getLast ()(0 |
| for (int j=1;j<=l;j++, i++) tmp1.append(i.getItem()) | |
| return | mod (mulNTL(buf1, buf2, b), M) |
| CanonicalForm | evalPoint (const CanonicalForm &F, CanonicalForm &eval, const Variable &alpha, CFList &list, const bool &GF, bool &fail) |
| find an evaluation point p, s.t. F(p,y) is squarefree and | |
| CFList | uniFactorizer (const CanonicalForm &A, const Variable &alpha, const bool &GF) |
| Univariate factorization of squarefree monic polys over finite fields via NTL. If the characteristic is even special GF2 routines of NTL are used. More... | |
| CFList | extFactorRecombination (CFList &factors, CanonicalForm &F, const CanonicalForm &N, const ExtensionInfo &info, DegreePattern °s, const CanonicalForm &eval, int s, int thres) |
| naive factor recombination as decribed in "Factoring
multivariate polynomials over a finite field" by L Bernardin. More... | |
| CFList | factorRecombination (CFList &factors, CanonicalForm &F, const CanonicalForm &N, DegreePattern °s, const CanonicalForm &eval, int s, int thres, const modpk &b, const CanonicalForm &den) |
| naive factor recombination as decribed in "Factoring
multivariate polynomials over a finite field" by L Bernardin. More... | |
| Variable | chooseExtension (const Variable &alpha, const Variable &beta, int k) |
| chooses a field extension. More... | |
| void | earlyFactorDetection (CFList &reconstructedFactors, CanonicalForm &F, CFList &factors, int &adaptedLiftBound, int *&factorsFoundIndex, DegreePattern °s, bool &success, int deg, const CanonicalForm &eval, const modpk &b, CanonicalForm &den) |
| void | earlyFactorDetection (CFList &reconstructedFactors, CanonicalForm &F, CFList &factors, int &adaptedLiftBound, int *&factorsFoundIndex, DegreePattern °s, bool &success, int deg, const CanonicalForm &eval, const modpk &b) |
| detects factors of F at stage deg of Hensel lifting. No combinations of more than one factor are tested. Lift bound and possible degree pattern are updated. More... | |
| void | extEarlyFactorDetection (CFList &reconstructedFactors, CanonicalForm &F, CFList &factors, int &adaptedLiftBound, int *&factorsFoundIndex, DegreePattern °s, bool &success, const ExtensionInfo &info, const CanonicalForm &eval, int deg) |
| detects factors of F at stage deg of Hensel lifting. No combinations of more than one factor are tested. Lift bound and possible degree pattern are updated. More... | |
| int * | getCombinations (int *rightSide, int sizeOfRightSide, int &sizeOfOutput, int degreeLC) |
| int * | getLiftPrecisions (const CanonicalForm &F, int &sizeOfOutput, int degreeLC) |
| compute lifting precisions from the shape of the Newton polygon of F More... | |
| void | deleteFactors (CFList &factors, int *factorsFoundIndex) |
| CFList | henselLiftAndEarly (CanonicalForm &A, bool &earlySuccess, CFList &earlyFactors, DegreePattern °s, int &liftBound, const CFList &uniFactors, const ExtensionInfo &info, const CanonicalForm &eval, modpk &b, CanonicalForm &den) |
| hensel Lifting and early factor detection More... | |
| CFList | henselLiftAndEarly (CanonicalForm &A, bool &earlySuccess, CFList &earlyFactors, DegreePattern °s, int &liftBound, const CFList &uniFactors, const ExtensionInfo &info, const CanonicalForm &eval) |
| hensel Lifting and early factor detection More... | |
| long | isReduced (const mat_zz_p &M) |
| long | isReduced (const nmod_mat_t M) |
| long | isReduced (const mat_zz_pE &M) |
| int * | extractZeroOneVecs (const mat_zz_p &M) |
| int * | extractZeroOneVecs (const nmod_mat_t M) |
| int * | extractZeroOneVecs (const mat_zz_pE &M) |
| void | reconstructionTry (CFList &reconstructedFactors, CanonicalForm &F, const CFList &factors, const int liftBound, int &factorsFound, int *&factorsFoundIndex, mat_zz_pE &N, const CanonicalForm &eval, bool beenInThres) |
| void | reconstructionTry (CFList &reconstructedFactors, CanonicalForm &F, const CFList &factors, const int liftBound, int &factorsFound, int *&factorsFoundIndex, mat_zz_p &N, const CanonicalForm &eval, bool beenInThres) |
| void | reconstructionTry (CFList &reconstructedFactors, CanonicalForm &F, const CFList &factors, const int liftBound, int &factorsFound, int *&factorsFoundIndex, nmod_mat_t N, const CanonicalForm &eval, bool beenInThres) |
| CFList | reconstruction (CanonicalForm &G, CFList &factors, int *zeroOneVecs, int precision, const mat_zz_pE &N, const CanonicalForm &eval) |
| CFList | monicReconstruction (CanonicalForm &G, CFList &factors, int *zeroOneVecs, int precision, const mat_zz_pE &N) |
| CFList | extReconstruction (CanonicalForm &G, CFList &factors, int *zeroOneVecs, int precision, const mat_zz_p &N, const ExtensionInfo &info, const CanonicalForm &evaluation) |
| CFList | extReconstruction (CanonicalForm &G, CFList &factors, int *zeroOneVecs, int precision, const nmod_mat_t N, const ExtensionInfo &info, const CanonicalForm &evaluation) |
| CFList | reconstruction (CanonicalForm &G, CFList &factors, int *zeroOneVecs, int precision, const mat_zz_p &N, const CanonicalForm &eval) |
| CFList | reconstruction (CanonicalForm &G, CFList &factors, int *zeroOneVecs, int precision, const nmod_mat_t N, const CanonicalForm &eval) |
| void | extReconstructionTry (CFList &reconstructedFactors, CanonicalForm &F, const CFList &factors, const int liftBound, int &factorsFound, int *&factorsFoundIndex, mat_zz_p &N, bool beenInThres, const ExtensionInfo &info, const CanonicalForm &evaluation) |
| void | extReconstructionTry (CFList &reconstructedFactors, CanonicalForm &F, const CFList &factors, const int liftBound, int &factorsFound, int *&factorsFoundIndex, nmod_mat_t N, bool beenInThres, const ExtensionInfo &info, const CanonicalForm &evaluation) |
| int | liftAndComputeLattice (const CanonicalForm &F, int *bounds, int sizeBounds, int start, int liftBound, int minBound, CFList &factors, mat_zz_p &NTLN, CFList &diophant, CFMatrix &M, CFArray &Pi, CFArray &bufQ, bool &irreducible) |
| int | liftAndComputeLattice (const CanonicalForm &F, int *bounds, int sizeBounds, int start, int liftBound, int minBound, CFList &factors, nmod_mat_t FLINTN, CFList &diophant, CFMatrix &M, CFArray &Pi, CFArray &bufQ, bool &irreducible) |
| int | extLiftAndComputeLattice (const CanonicalForm &F, int *bounds, int sizeBounds, int liftBound, int minBound, int start, CFList &factors, mat_zz_p &NTLN, CFList &diophant, CFMatrix &M, CFArray &Pi, CFArray &bufQ, bool &irreducible, const CanonicalForm &evaluation, const ExtensionInfo &info, CFList &source, CFList &dest) |
| int | extLiftAndComputeLattice (const CanonicalForm &F, int *bounds, int sizeBounds, int liftBound, int minBound, int start, CFList &factors, nmod_mat_t FLINTN, CFList &diophant, CFMatrix &M, CFArray &Pi, CFArray &bufQ, bool &irreducible, const CanonicalForm &evaluation, const ExtensionInfo &info, CFList &source, CFList &dest) |
| int | liftAndComputeLattice (const CanonicalForm &F, int *bounds, int sizeBounds, int start, int liftBound, int minBound, CFList &factors, mat_zz_pE &NTLN, CFList &diophant, CFMatrix &M, CFArray &Pi, CFArray &bufQ, bool &irreducible) |
| int | liftAndComputeLatticeFq2Fp (const CanonicalForm &F, int *bounds, int sizeBounds, int start, int liftBound, int minBound, CFList &factors, nmod_mat_t FLINTN, CFList &diophant, CFMatrix &M, CFArray &Pi, CFArray &bufQ, bool &irreducible, const Variable &alpha) |
| CFList | increasePrecision (CanonicalForm &F, CFList &factors, int factorsFound, int oldNumCols, int oldL, int precision, const CanonicalForm &eval) |
| CFList | increasePrecision (CanonicalForm &F, CFList &factors, int factorsFound, int oldNumCols, int oldL, const Variable &, int precision, const CanonicalForm &eval) |
| CFList | extIncreasePrecision (CanonicalForm &F, CFList &factors, int factorsFound, int oldNumCols, int oldL, const CanonicalForm &evaluation, const ExtensionInfo &info, CFList &source, CFList &dest, int precision) |
| CFList | increasePrecision2 (const CanonicalForm &F, CFList &factors, const Variable &alpha, int precision) |
| CFList | increasePrecisionFq2Fp (CanonicalForm &F, CFList &factors, int factorsFound, int oldNumCols, int oldL, const Variable &alpha, int precision, const CanonicalForm &eval) |
| CFList | increasePrecision (CanonicalForm &F, CFList &factors, int oldL, int l, int d, int *bounds, CFArray &bufQ, nmod_mat_t FLINTN, const CanonicalForm &eval) |
| CFList | increasePrecision (CanonicalForm &F, CFList &factors, int oldL, int l, int d, int *bounds, CFArray &bufQ, mat_zz_pE &NTLN, const CanonicalForm &eval) |
| CFList | extIncreasePrecision (CanonicalForm &F, CFList &factors, int oldL, int l, int d, int *bounds, CFArray &bufQ, nmod_mat_t FLINTN, const CanonicalForm &evaluation, const ExtensionInfo &info, CFList &source, CFList &dest) |
| CFList | increasePrecisionFq2Fp (CanonicalForm &F, CFList &factors, int oldL, int l, int d, int *bounds, CFArray &bufQ, nmod_mat_t FLINTN, const Variable &alpha, const CanonicalForm &eval) |
| CFList | furtherLiftingAndIncreasePrecision (CanonicalForm &F, CFList &factors, int l, int liftBound, int d, int *bounds, nmod_mat_t FLINTN, CFList &diophant, CFMatrix &M, CFArray &Pi, CFArray &bufQ, const CanonicalForm &eval) |
| CFList | furtherLiftingAndIncreasePrecision (CanonicalForm &F, CFList &factors, int l, int liftBound, int d, int *bounds, mat_zz_pE &NTLN, CFList &diophant, CFMatrix &M, CFArray &Pi, CFArray &bufQ, const CanonicalForm &eval) |
| CFList | extFurtherLiftingAndIncreasePrecision (CanonicalForm &F, CFList &factors, int l, int liftBound, int d, int *bounds, nmod_mat_t FLINTN, CFList &diophant, CFMatrix &M, CFArray &Pi, CFArray &bufQ, const CanonicalForm &evaluation, const ExtensionInfo &info, CFList &source, CFList &dest) |
| CFList | furtherLiftingAndIncreasePrecisionFq2Fp (CanonicalForm &F, CFList &factors, int l, int liftBound, int d, int *bounds, nmod_mat_t FLINTN, CFList &diophant, CFMatrix &M, CFArray &Pi, CFArray &bufQ, const Variable &alpha, const CanonicalForm &eval) |
| void | refineAndRestartLift (const CanonicalForm &F, const nmod_mat_t FLINTN, int liftBound, int l, CFList &factors, CFMatrix &M, CFArray &Pi, CFList &diophant) |
| void | refineAndRestartLift (const CanonicalForm &F, const mat_zz_pE &NTLN, int liftBound, int l, CFList &factors, CFMatrix &M, CFArray &Pi, CFList &diophant) |
| CFList | earlyReconstructionAndLifting (const CanonicalForm &F, const nmod_mat_t N, CanonicalForm &bufF, CFList &factors, int &l, int &factorsFound, bool beenInThres, CFMatrix &M, CFArray &Pi, CFList &diophant, bool symmetric, const CanonicalForm &evaluation) |
| CFList | earlyReconstructionAndLifting (const CanonicalForm &F, const mat_zz_pE &N, CanonicalForm &bufF, CFList &factors, int &l, int &factorsFound, bool beenInThres, CFMatrix &M, CFArray &Pi, CFList &diophant, bool symmetric, const CanonicalForm &evaluation) |
| CFList | extEarlyReconstructionAndLifting (const CanonicalForm &F, const nmod_mat_t N, CanonicalForm &bufF, CFList &factors, int &l, int &factorsFound, bool beenInThres, CFMatrix &M, CFArray &Pi, CFList &diophant, const ExtensionInfo &info, const CanonicalForm &evaluation) |
| CFList | sieveSmallFactors (const CanonicalForm &G, CFList &uniFactors, DegreePattern °Pat, CanonicalForm &H, CFList &diophant, CFArray &Pi, CFMatrix &M, bool &success, int d, const CanonicalForm &eval) |
| CFList | extSieveSmallFactors (const CanonicalForm &G, CFList &uniFactors, DegreePattern °Pat, CanonicalForm &H, CFList &diophant, CFArray &Pi, CFMatrix &M, bool &success, int d, const CanonicalForm &evaluation, const ExtensionInfo &info) |
| CFList | henselLiftAndLatticeRecombi (const CanonicalForm &G, const CFList &uniFactors, const Variable &alpha, const DegreePattern °Pat, bool symmetric, const CanonicalForm &eval) |
| ExtensionInfo | init4ext (const ExtensionInfo &info, const CanonicalForm &evaluation, int °Mipo) |
| CFList | extHenselLiftAndLatticeRecombi (const CanonicalForm &G, const CFList &uniFactors, const ExtensionInfo &extInfo, const DegreePattern °Pat, const CanonicalForm &eval) |
| CFList | extBiFactorize (const CanonicalForm &F, const ExtensionInfo &info) |
| Factorization over an extension of initial field. More... | |
| CFList | biFactorize (const CanonicalForm &F, const ExtensionInfo &info) |
| bivariate factorization over finite fields as decribed in "Factoring
multivariate polynomials over a finite field" by L Bernardin. More... | |
Variables | |
| const CanonicalForm & | M |
| const CanonicalForm const modpk & | b |
| else | |
| CFListIterator | i = L |
| CFList | tmp1 |
| CFList | tmp2 = Difference (L, tmp1) |
| CanonicalForm | buf1 = prodMod0 (tmp1, M, b) |
| CanonicalForm | buf2 = prodMod0 (tmp2, M, b) |
This file provides functions for factorizing a bivariate polynomial over 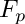
Bernardin. Factor Recombination is described in "Factoring polynomials over global fields" by K. Belabas, M. van Hoeij, J. Klueners, A. Steel
Definition in file facFqBivar.cc.
| CFList biFactorize | ( | const CanonicalForm & | F, |
| const ExtensionInfo & | info | ||
| ) |
bivariate factorization over finite fields as decribed in "Factoring multivariate polynomials over a finite field" by L Bernardin.
Factorization of a squarefree bivariate polynomials over an arbitrary finite field, information on the current field we work over is in info. info may also contain information about the initial field if initial and current field do not coincide. In this case the current field is an extension of the initial field and the factors returned are factors of F over the initial field.
| [in] | F | a sqrfree bivariate poly |
| [in] | info | information about extension |
Definition at line 8303 of file facFqBivar.cc.
chooses a field extension.
| [in] | alpha | some algebraic variable |
| [in] | beta | some algebraic variable |
| [in] | k | some int |
Definition at line 806 of file facFqBivar.cc.
| void deleteFactors | ( | CFList & | factors, |
| int * | factorsFoundIndex | ||
| ) |
Definition at line 1136 of file facFqBivar.cc.
| void earlyFactorDetection | ( | CFList & | reconstructedFactors, |
| CanonicalForm & | F, | ||
| CFList & | factors, | ||
| int & | adaptedLiftBound, | ||
| int *& | factorsFoundIndex, | ||
| DegreePattern & | degs, | ||
| bool & | success, | ||
| int | deg, | ||
| const CanonicalForm & | eval, | ||
| const modpk & | b = modpk() |
||
| ) |
detects factors of F at stage deg of Hensel lifting. No combinations of more than one factor are tested. Lift bound and possible degree pattern are updated.
| [in,out] | reconstructedFactors | list of reconstructed factors |
| [in,out] | F | poly to be factored, returns poly divided by detected factors in case of success |
| [in,out] | factors | list of factors lifted up to deg, returns a list of factors without detected factors |
| [in,out] | adaptedLiftBound | adapted lift bound |
| [in,out] | factorsFoundIndex | factors already considered |
| [in,out] | degs | degree pattern, is updated whenever we find a factor |
| [in,out] | success | indicating success |
| [in] | deg | stage of Hensel lifting |
| [in] | eval | evaluation point |
| [in] | b | coeff bound |
Definition at line 971 of file facFqBivar.cc.
| void earlyFactorDetection | ( | CFList & | reconstructedFactors, |
| CanonicalForm & | F, | ||
| CFList & | factors, | ||
| int & | adaptedLiftBound, | ||
| int *& | factorsFoundIndex, | ||
| DegreePattern & | degs, | ||
| bool & | success, | ||
| int | deg, | ||
| const CanonicalForm & | eval, | ||
| const modpk & | b, | ||
| CanonicalForm & | den | ||
| ) |
Definition at line 852 of file facFqBivar.cc.
| CFList earlyReconstructionAndLifting | ( | const CanonicalForm & | F, |
| const mat_zz_pE & | N, | ||
| CanonicalForm & | bufF, | ||
| CFList & | factors, | ||
| int & | l, | ||
| int & | factorsFound, | ||
| bool | beenInThres, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFList & | diophant, | ||
| bool | symmetric, | ||
| const CanonicalForm & | evaluation | ||
| ) |
Definition at line 6419 of file facFqBivar.cc.
| CFList earlyReconstructionAndLifting | ( | const CanonicalForm & | F, |
| const nmod_mat_t | N, | ||
| CanonicalForm & | bufF, | ||
| CFList & | factors, | ||
| int & | l, | ||
| int & | factorsFound, | ||
| bool | beenInThres, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFList & | diophant, | ||
| bool | symmetric, | ||
| const CanonicalForm & | evaluation | ||
| ) |
Definition at line 6205 of file facFqBivar.cc.
| CanonicalForm evalPoint | ( | const CanonicalForm & | F, |
| CanonicalForm & | eval, | ||
| const Variable & | alpha, | ||
| CFList & | list, | ||
| const bool & | GF, | ||
| bool & | fail | ||
| ) |
find an evaluation point p, s.t. F(p,y) is squarefree and 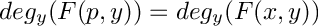
| [in] | F | compressed, bivariate poly |
| [in,out] | eval | F (p, y) |
| [in] | alpha | algebraic variable |
| [in] | list | list of points already considered |
| [in] | GF | GaloisFieldDomain? |
| [in,out] | fail | equals true, if there is no valid evaluation point |
Definition at line 84 of file facFqBivar.cc.
| CFList extBiFactorize | ( | const CanonicalForm & | F, |
| const ExtensionInfo & | info | ||
| ) |
Factorization over an extension of initial field.
| [in] | F | poly to be factored |
| [in] | info | info about extension |
Definition at line 8928 of file facFqBivar.cc.
| void extEarlyFactorDetection | ( | CFList & | reconstructedFactors, |
| CanonicalForm & | F, | ||
| CFList & | factors, | ||
| int & | adaptedLiftBound, | ||
| int *& | factorsFoundIndex, | ||
| DegreePattern & | degs, | ||
| bool & | success, | ||
| const ExtensionInfo & | info, | ||
| const CanonicalForm & | eval, | ||
| int | deg | ||
| ) |
detects factors of F at stage deg of Hensel lifting. No combinations of more than one factor are tested. Lift bound and possible degree pattern are updated.
| [in,out] | reconstructedFactors | list of reconstructed factors |
| [in,out] | F | poly to be factored, returns poly divided by detected factors in case of success |
| [in,out] | factors | list of factors lifted up to deg, returns a list of factors without detected factors |
| [in,out] | adaptedLiftBound | adapted lift bound |
| [in,out] | factorsFoundIndex | factors already considered |
| [in,out] | degs | degree pattern, is updated whenever we find a factor |
| [in,out] | success | indicating success |
| [in] | info | information about extension |
| [in] | eval | evaluation point |
| [in] | deg | stage of Hensel lifting |
Definition at line 982 of file facFqBivar.cc.
| CFList extEarlyReconstructionAndLifting | ( | const CanonicalForm & | F, |
| const nmod_mat_t | N, | ||
| CanonicalForm & | bufF, | ||
| CFList & | factors, | ||
| int & | l, | ||
| int & | factorsFound, | ||
| bool | beenInThres, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFList & | diophant, | ||
| const ExtensionInfo & | info, | ||
| const CanonicalForm & | evaluation | ||
| ) |
Definition at line 6579 of file facFqBivar.cc.
| CFList extFactorRecombination | ( | CFList & | factors, |
| CanonicalForm & | F, | ||
| const CanonicalForm & | N, | ||
| const ExtensionInfo & | info, | ||
| DegreePattern & | degs, | ||
| const CanonicalForm & | eval, | ||
| int | s, | ||
| int | thres | ||
| ) |
naive factor recombination as decribed in "Factoring multivariate polynomials over a finite field" by L Bernardin.
naive factor recombination over an extension of the initial field. Uses precomputed data to exclude combinations that are not possible.
| [in,out] | factors | list of lifted factors that are monic wrt Variable (1), original factors-factors found |
| [in,out] | F | poly to be factored, F/factors found |
| [in] | N | Variable (2)^liftBound |
| [in] | info | contains information about extension |
| [in] | eval | evaluation point |
| [in] | s | algorithm starts checking subsets of size s |
| [in] | thres | threshold for the size of subsets which are checked, for a full factor recombination choose thres= factors.length()/2 |
Definition at line 370 of file facFqBivar.cc.
| CFList extFurtherLiftingAndIncreasePrecision | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | l, | ||
| int | liftBound, | ||
| int | d, | ||
| int * | bounds, | ||
| nmod_mat_t | FLINTN, | ||
| CFList & | diophant, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFArray & | bufQ, | ||
| const CanonicalForm & | evaluation, | ||
| const ExtensionInfo & | info, | ||
| CFList & | source, | ||
| CFList & | dest | ||
| ) |
Definition at line 5557 of file facFqBivar.cc.
| CFList extHenselLiftAndLatticeRecombi | ( | const CanonicalForm & | G, |
| const CFList & | uniFactors, | ||
| const ExtensionInfo & | extInfo, | ||
| const DegreePattern & | degPat, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 7712 of file facFqBivar.cc.
| CFList extIncreasePrecision | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | factorsFound, | ||
| int | oldNumCols, | ||
| int | oldL, | ||
| const CanonicalForm & | evaluation, | ||
| const ExtensionInfo & | info, | ||
| CFList & | source, | ||
| CFList & | dest, | ||
| int | precision | ||
| ) |
Definition at line 3826 of file facFqBivar.cc.
| CFList extIncreasePrecision | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | oldL, | ||
| int | l, | ||
| int | d, | ||
| int * | bounds, | ||
| CFArray & | bufQ, | ||
| nmod_mat_t | FLINTN, | ||
| const CanonicalForm & | evaluation, | ||
| const ExtensionInfo & | info, | ||
| CFList & | source, | ||
| CFList & | dest | ||
| ) |
Definition at line 4756 of file facFqBivar.cc.
| int extLiftAndComputeLattice | ( | const CanonicalForm & | F, |
| int * | bounds, | ||
| int | sizeBounds, | ||
| int | liftBound, | ||
| int | minBound, | ||
| int | start, | ||
| CFList & | factors, | ||
| mat_zz_p & | NTLN, | ||
| CFList & | diophant, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFArray & | bufQ, | ||
| bool & | irreducible, | ||
| const CanonicalForm & | evaluation, | ||
| const ExtensionInfo & | info, | ||
| CFList & | source, | ||
| CFList & | dest | ||
| ) |
Definition at line 2749 of file facFqBivar.cc.
| int extLiftAndComputeLattice | ( | const CanonicalForm & | F, |
| int * | bounds, | ||
| int | sizeBounds, | ||
| int | liftBound, | ||
| int | minBound, | ||
| int | start, | ||
| CFList & | factors, | ||
| nmod_mat_t | FLINTN, | ||
| CFList & | diophant, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFArray & | bufQ, | ||
| bool & | irreducible, | ||
| const CanonicalForm & | evaluation, | ||
| const ExtensionInfo & | info, | ||
| CFList & | source, | ||
| CFList & | dest | ||
| ) |
Definition at line 2948 of file facFqBivar.cc.
| int * extractZeroOneVecs | ( | const mat_zz_p & | M | ) |
Definition at line 1525 of file facFqBivar.cc.
| int * extractZeroOneVecs | ( | const mat_zz_pE & | M | ) |
Definition at line 1577 of file facFqBivar.cc.
| int * extractZeroOneVecs | ( | const nmod_mat_t | M | ) |
Definition at line 1551 of file facFqBivar.cc.
| CFList extReconstruction | ( | CanonicalForm & | G, |
| CFList & | factors, | ||
| int * | zeroOneVecs, | ||
| int | precision, | ||
| const mat_zz_p & | N, | ||
| const ExtensionInfo & | info, | ||
| const CanonicalForm & | evaluation | ||
| ) |
Definition at line 1960 of file facFqBivar.cc.
| CFList extReconstruction | ( | CanonicalForm & | G, |
| CFList & | factors, | ||
| int * | zeroOneVecs, | ||
| int | precision, | ||
| const nmod_mat_t | N, | ||
| const ExtensionInfo & | info, | ||
| const CanonicalForm & | evaluation | ||
| ) |
Definition at line 2041 of file facFqBivar.cc.
| void extReconstructionTry | ( | CFList & | reconstructedFactors, |
| CanonicalForm & | F, | ||
| const CFList & | factors, | ||
| const int | liftBound, | ||
| int & | factorsFound, | ||
| int *& | factorsFoundIndex, | ||
| mat_zz_p & | N, | ||
| bool | beenInThres, | ||
| const ExtensionInfo & | info, | ||
| const CanonicalForm & | evaluation | ||
| ) |
Definition at line 2224 of file facFqBivar.cc.
| void extReconstructionTry | ( | CFList & | reconstructedFactors, |
| CanonicalForm & | F, | ||
| const CFList & | factors, | ||
| const int | liftBound, | ||
| int & | factorsFound, | ||
| int *& | factorsFoundIndex, | ||
| nmod_mat_t | N, | ||
| bool | beenInThres, | ||
| const ExtensionInfo & | info, | ||
| const CanonicalForm & | evaluation | ||
| ) |
Definition at line 2354 of file facFqBivar.cc.
| CFList extSieveSmallFactors | ( | const CanonicalForm & | G, |
| CFList & | uniFactors, | ||
| DegreePattern & | degPat, | ||
| CanonicalForm & | H, | ||
| CFList & | diophant, | ||
| CFArray & | Pi, | ||
| CFMatrix & | M, | ||
| bool & | success, | ||
| int | d, | ||
| const CanonicalForm & | evaluation, | ||
| const ExtensionInfo & | info | ||
| ) |
Definition at line 6809 of file facFqBivar.cc.
| CFList factorRecombination | ( | CFList & | factors, |
| CanonicalForm & | F, | ||
| const CanonicalForm & | N, | ||
| DegreePattern & | degs, | ||
| const CanonicalForm & | eval, | ||
| int | s, | ||
| int | thres, | ||
| const modpk & | b, | ||
| const CanonicalForm & | den | ||
| ) |
naive factor recombination as decribed in "Factoring multivariate polynomials over a finite field" by L Bernardin.
naive factor recombination. Uses precomputed data to exclude combinations that are not possible.
| [in,out] | factors | list of lifted factors that are monic wrt Variable (1) |
| [in,out] | F | poly to be factored |
| [in] | N | Variable (2)^liftBound |
| [in] | degs | degree pattern |
| [in] | eval | evaluation point |
| [in] | s | algorithm starts checking subsets of size s |
| [in] | thres | threshold for the size of subsets which are checked, for a full factor recombination choose thres= factors.length()/2 |
| [in] | b | coeff bound |
| [in] | den | bound on the den if over Q (a) |
Definition at line 586 of file facFqBivar.cc.
| CFList furtherLiftingAndIncreasePrecision | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | l, | ||
| int | liftBound, | ||
| int | d, | ||
| int * | bounds, | ||
| mat_zz_pE & | NTLN, | ||
| CFList & | diophant, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFArray & | bufQ, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 5409 of file facFqBivar.cc.
| CFList furtherLiftingAndIncreasePrecision | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | l, | ||
| int | liftBound, | ||
| int | d, | ||
| int * | bounds, | ||
| nmod_mat_t | FLINTN, | ||
| CFList & | diophant, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFArray & | bufQ, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 5174 of file facFqBivar.cc.
| CFList furtherLiftingAndIncreasePrecisionFq2Fp | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | l, | ||
| int | liftBound, | ||
| int | d, | ||
| int * | bounds, | ||
| nmod_mat_t | FLINTN, | ||
| CFList & | diophant, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFArray & | bufQ, | ||
| const Variable & | alpha, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 5873 of file facFqBivar.cc.
| int * getCombinations | ( | int * | rightSide, |
| int | sizeOfRightSide, | ||
| int & | sizeOfOutput, | ||
| int | degreeLC | ||
| ) |
Definition at line 1081 of file facFqBivar.cc.
| else L getLast | ( | ) |
| int * getLiftPrecisions | ( | const CanonicalForm & | F, |
| int & | sizeOfOutput, | ||
| int | degreeLC | ||
| ) |
compute lifting precisions from the shape of the Newton polygon of F
| [in] | F | a bivariate poly |
| [in,out] | sizeOfOutput | size of the output |
| [in] | degreeLC | degree of the leading coeff [in] of F wrt. Variable (1) |
Definition at line 1120 of file facFqBivar.cc.
| CFList henselLiftAndEarly | ( | CanonicalForm & | A, |
| bool & | earlySuccess, | ||
| CFList & | earlyFactors, | ||
| DegreePattern & | degs, | ||
| int & | liftBound, | ||
| const CFList & | uniFactors, | ||
| const ExtensionInfo & | info, | ||
| const CanonicalForm & | eval | ||
| ) |
hensel Lifting and early factor detection
| [in,out] | A | poly to be factored, returns poly divided by detected factors in case of success |
| [in,out] | earlySuccess | indicating success |
| [in,out] | earlyFactors | list of factors detected at early stage of Hensel lifting |
| [in,out] | degs | degree pattern |
| [in,out] | liftBound | (adapted) lift bound |
| [in] | uniFactors | univariate factors |
| [in] | info | information about extension |
| [in] | eval | evaluation point |
Definition at line 1455 of file facFqBivar.cc.
| CFList henselLiftAndEarly | ( | CanonicalForm & | A, |
| bool & | earlySuccess, | ||
| CFList & | earlyFactors, | ||
| DegreePattern & | degs, | ||
| int & | liftBound, | ||
| const CFList & | uniFactors, | ||
| const ExtensionInfo & | info, | ||
| const CanonicalForm & | eval, | ||
| modpk & | b, | ||
| CanonicalForm & | den | ||
| ) |
hensel Lifting and early factor detection
| [in,out] | A | poly to be factored, returns poly divided by detected factors in case of success |
| [in,out] | earlySuccess | indicating success |
| [in,out] | earlyFactors | list of factors detected at early stage of Hensel lifting |
| [in,out] | degs | degree pattern |
| [in,out] | liftBound | (adapted) lift bound |
| [in] | uniFactors | univariate factors |
| [in] | info | information about extension |
| [in] | eval | evaluation point |
| [in] | b | coeff bound |
| [in] | den | bound on the den if over Q(a) |
Definition at line 1152 of file facFqBivar.cc.
| CFList henselLiftAndLatticeRecombi | ( | const CanonicalForm & | G, |
| const CFList & | uniFactors, | ||
| const Variable & | alpha, | ||
| const DegreePattern & | degPat, | ||
| bool | symmetric, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 6859 of file facFqBivar.cc.
| else if | ( | L. | length() = = 1 | ) |
| CFList increasePrecision | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | factorsFound, | ||
| int | oldNumCols, | ||
| int | oldL, | ||
| const Variable & | , | ||
| int | precision, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 3684 of file facFqBivar.cc.
| CFList increasePrecision | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | factorsFound, | ||
| int | oldNumCols, | ||
| int | oldL, | ||
| int | precision, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 3475 of file facFqBivar.cc.
| CFList increasePrecision | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | oldL, | ||
| int | l, | ||
| int | d, | ||
| int * | bounds, | ||
| CFArray & | bufQ, | ||
| mat_zz_pE & | NTLN, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 4647 of file facFqBivar.cc.
| CFList increasePrecision | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | oldL, | ||
| int | l, | ||
| int | d, | ||
| int * | bounds, | ||
| CFArray & | bufQ, | ||
| nmod_mat_t | FLINTN, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 4478 of file facFqBivar.cc.
| CFList increasePrecision2 | ( | const CanonicalForm & | F, |
| CFList & | factors, | ||
| const Variable & | alpha, | ||
| int | precision | ||
| ) |
Definition at line 4134 of file facFqBivar.cc.
| CFList increasePrecisionFq2Fp | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | factorsFound, | ||
| int | oldNumCols, | ||
| int | oldL, | ||
| const Variable & | alpha, | ||
| int | precision, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 4267 of file facFqBivar.cc.
| CFList increasePrecisionFq2Fp | ( | CanonicalForm & | F, |
| CFList & | factors, | ||
| int | oldL, | ||
| int | l, | ||
| int | d, | ||
| int * | bounds, | ||
| CFArray & | bufQ, | ||
| nmod_mat_t | FLINTN, | ||
| const Variable & | alpha, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 5014 of file facFqBivar.cc.
| ExtensionInfo init4ext | ( | const ExtensionInfo & | info, |
| const CanonicalForm & | evaluation, | ||
| int & | degMipo | ||
| ) |
Definition at line 7657 of file facFqBivar.cc.
| long isReduced | ( | const mat_zz_p & | M | ) |
Definition at line 1468 of file facFqBivar.cc.
| long isReduced | ( | const mat_zz_pE & | M | ) |
Definition at line 1506 of file facFqBivar.cc.
| long isReduced | ( | const nmod_mat_t | M | ) |
Definition at line 1487 of file facFqBivar.cc.
| int liftAndComputeLattice | ( | const CanonicalForm & | F, |
| int * | bounds, | ||
| int | sizeBounds, | ||
| int | start, | ||
| int | liftBound, | ||
| int | minBound, | ||
| CFList & | factors, | ||
| mat_zz_p & | NTLN, | ||
| CFList & | diophant, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFArray & | bufQ, | ||
| bool & | irreducible | ||
| ) |
Definition at line 2485 of file facFqBivar.cc.
| int liftAndComputeLattice | ( | const CanonicalForm & | F, |
| int * | bounds, | ||
| int | sizeBounds, | ||
| int | start, | ||
| int | liftBound, | ||
| int | minBound, | ||
| CFList & | factors, | ||
| mat_zz_pE & | NTLN, | ||
| CFList & | diophant, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFArray & | bufQ, | ||
| bool & | irreducible | ||
| ) |
Definition at line 3157 of file facFqBivar.cc.
| int liftAndComputeLattice | ( | const CanonicalForm & | F, |
| int * | bounds, | ||
| int | sizeBounds, | ||
| int | start, | ||
| int | liftBound, | ||
| int | minBound, | ||
| CFList & | factors, | ||
| nmod_mat_t | FLINTN, | ||
| CFList & | diophant, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFArray & | bufQ, | ||
| bool & | irreducible | ||
| ) |
Definition at line 2610 of file facFqBivar.cc.
| int liftAndComputeLatticeFq2Fp | ( | const CanonicalForm & | F, |
| int * | bounds, | ||
| int | sizeBounds, | ||
| int | start, | ||
| int | liftBound, | ||
| int | minBound, | ||
| CFList & | factors, | ||
| nmod_mat_t | FLINTN, | ||
| CFList & | diophant, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFArray & | bufQ, | ||
| bool & | irreducible, | ||
| const Variable & | alpha | ||
| ) |
Definition at line 3292 of file facFqBivar.cc.
| CFList monicReconstruction | ( | CanonicalForm & | G, |
| CFList & | factors, | ||
| int * | zeroOneVecs, | ||
| int | precision, | ||
| const mat_zz_pE & | N | ||
| ) |
Definition at line 1907 of file facFqBivar.cc.
| CFList reconstruction | ( | CanonicalForm & | G, |
| CFList & | factors, | ||
| int * | zeroOneVecs, | ||
| int | precision, | ||
| const mat_zz_p & | N, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 2122 of file facFqBivar.cc.
| CFList reconstruction | ( | CanonicalForm & | G, |
| CFList & | factors, | ||
| int * | zeroOneVecs, | ||
| int | precision, | ||
| const mat_zz_pE & | N, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 1856 of file facFqBivar.cc.
| CFList reconstruction | ( | CanonicalForm & | G, |
| CFList & | factors, | ||
| int * | zeroOneVecs, | ||
| int | precision, | ||
| const nmod_mat_t | N, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 2173 of file facFqBivar.cc.
| void reconstructionTry | ( | CFList & | reconstructedFactors, |
| CanonicalForm & | F, | ||
| const CFList & | factors, | ||
| const int | liftBound, | ||
| int & | factorsFound, | ||
| int *& | factorsFoundIndex, | ||
| mat_zz_p & | N, | ||
| const CanonicalForm & | eval, | ||
| bool | beenInThres | ||
| ) |
Definition at line 1688 of file facFqBivar.cc.
| void reconstructionTry | ( | CFList & | reconstructedFactors, |
| CanonicalForm & | F, | ||
| const CFList & | factors, | ||
| const int | liftBound, | ||
| int & | factorsFound, | ||
| int *& | factorsFoundIndex, | ||
| mat_zz_pE & | N, | ||
| const CanonicalForm & | eval, | ||
| bool | beenInThres | ||
| ) |
Definition at line 1604 of file facFqBivar.cc.
| void reconstructionTry | ( | CFList & | reconstructedFactors, |
| CanonicalForm & | F, | ||
| const CFList & | factors, | ||
| const int | liftBound, | ||
| int & | factorsFound, | ||
| int *& | factorsFoundIndex, | ||
| nmod_mat_t | N, | ||
| const CanonicalForm & | eval, | ||
| bool | beenInThres | ||
| ) |
Definition at line 1772 of file facFqBivar.cc.
| void refineAndRestartLift | ( | const CanonicalForm & | F, |
| const mat_zz_pE & | NTLN, | ||
| int | liftBound, | ||
| int | l, | ||
| CFList & | factors, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFList & | diophant | ||
| ) |
| void refineAndRestartLift | ( | const CanonicalForm & | F, |
| const nmod_mat_t | FLINTN, | ||
| int | liftBound, | ||
| int | l, | ||
| CFList & | factors, | ||
| CFMatrix & | M, | ||
| CFArray & | Pi, | ||
| CFList & | diophant | ||
| ) |
| CFList sieveSmallFactors | ( | const CanonicalForm & | G, |
| CFList & | uniFactors, | ||
| DegreePattern & | degPat, | ||
| CanonicalForm & | H, | ||
| CFList & | diophant, | ||
| CFArray & | Pi, | ||
| CFMatrix & | M, | ||
| bool & | success, | ||
| int | d, | ||
| const CanonicalForm & | eval | ||
| ) |
Definition at line 6762 of file facFqBivar.cc.
| TIMING_DEFINE_PRINT | ( | fac_fq_uni_factorizer | ) | const & |
Univariate factorization of squarefree monic polys over finite fields via NTL. If the characteristic is even special GF2 routines of NTL are used.
| [in] | A | squarefree univariate poly |
| [in] | alpha | algebraic variable |
| [in] | GF | GaloisFieldDomain? |
Definition at line 160 of file facFqBivar.cc.
| else L b |
Definition at line 60 of file facFqBivar.cc.
| else |
Definition at line 68 of file facFqBivar.cc.
| CFListIterator i = L |
Definition at line 71 of file facFqBivar.cc.
| else L M |
Definition at line 60 of file facFqBivar.cc.
| CFList tmp1 |
Definition at line 72 of file facFqBivar.cc.
| tmp2 = Difference (L, tmp1) |
Definition at line 72 of file facFqBivar.cc.