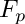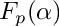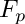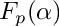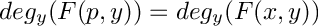Factorization of a squarefree bivariate polynomials over an arbitrary finite field, information on the current field we work over is in info. info may also contain information about the initial field if initial and current field do not coincide. In this case the current field is an extension of the initial field and the factors returned are factors of F over the initial field.
Factorization of a squarefree bivariate polynomials over an arbitrary finite field, information on the current field we work over is in info. info may also contain information about the initial field if initial and current field do not coincide. In this case the current field is an extension of the initial field and the factors returned are factors of F over the initial field.
8304{
8307
8310
8315 int k=
info.getGFDegree();
8316 bool extension=
info.isInExtension();
8317 if (
A.isUnivariate())
8318 {
8319 if (extension == false)
8321 else
8322 {
8326 }
8327 }
8328
8332
8335
8336
8339
8340 A=
A/(contentAx*contentAy);
8341 CFList contentAxFactors, contentAyFactors;
8342
8343 if (!extension)
8344 {
8347 }
8348
8349
8351 if (
A.inCoeffDomain())
8352 {
8353 append (factors, contentAxFactors);
8354 append (factors, contentAyFactors);
8356 return factors;
8357 }
8358 else if (
A.isUnivariate())
8359 {
8361 append (factors, contentAxFactors);
8362 append (factors, contentAyFactors);
8364 return factors;
8365 }
8366
8367
8368
8371 {
8373
8376
8377 if (!extension)
8379 return factors;
8380 }
8381
8382
8383 bool derivXZero= false;
8387 derivXZero= true;
8388 else
8389 {
8390 gcdDerivX=
gcd (
A, derivX);
8391 if (
degree (gcdDerivX) > 0)
8392 {
8396 append (factorsG, contentAxFactors);
8397 append (factorsG, contentAyFactors);
8399 if (!extension)
8401 return factorsG;
8402 }
8403 }
8404 bool derivYZero= false;
8408 derivYZero= true;
8409 else
8410 {
8411 gcdDerivY=
gcd (
A, derivY);
8412 if (
degree (gcdDerivY) > 0)
8413 {
8417 append (factorsG, contentAxFactors);
8418 append (factorsG, contentAyFactors);
8420 if (!extension)
8422 return factorsG;
8423 }
8424 }
8425
8428 {
8429 if (!derivYZero)
8430 {
8433 derivXZero= derivYZero;
8436 }
8437 }
8438
8439 int boundsLength;
8443 {
8444 delete [] bounds;
8446
8449
8450 if (!extension)
8452 return factors;
8453 }
8454
8455 int minBound= bounds[0];
8456 for (
int i= 1;
i < boundsLength;
i++)
8457 {
8459 minBound=
tmin (minBound, bounds[
i]);
8460 }
8461
8462 int boundsLength2;
8464 int minBound2= bounds2[0];
8465 for (
int i= 1;
i < boundsLength2;
i++)
8466 {
8467 if (bounds2[
i] != 0)
8468 minBound2=
tmin (minBound2, bounds2[
i]);
8469 }
8470
8471
8472 bool fail= false;
8474 CFList uniFactors, list, bufUniFactors;
8477
8478 bool fail2= false;
8479 CanonicalForm Aeval2, evaluation2, bufAeval2, bufEvaluation2;
8480 CFList bufUniFactors2, list2, uniFactors2;
8483 bool swap2= false;
8484
8485
8486
8487
8488 int factorNums= 3;
8491 bool symmetric= false;
8492
8494 for (
int i= 0;
i < factorNums;
i++)
8495 {
8500 if (!derivXZero && !fail2 && !symmetric)
8501 {
8503 {
8506 }
8511 "time to find eval point wrt y: ");
8512 }
8513
8514 if (fail && (
i == 0))
8515 {
8516 if (!derivXZero && !fail2 && !symmetric)
8517 {
8518 bufEvaluation= bufEvaluation2;
8519 int dummy= subCheck2;
8520 subCheck2= subCheck1;
8521 subCheck1= dummy;
8525 bufAeval= bufAeval2;
8526 swap2= true;
8527 fail= false;
8528 }
8529 else
8530 fail= true;
8531 }
8532
8533
8534 if (fail && (
i == 0))
8535 {
8540 delete [] bounds;
8541 delete [] bounds2;
8542 return factors;
8543 }
8544
8545
8546
8547 if (fail && (
i != 0))
8548 break;
8549
8550
8554 "time for univariate factorization over Fq: ");
8555 DEBOUTLN (cerr,
"Lc (bufAeval)*prod (bufUniFactors)== bufAeval " <<
8556 (
prod (bufUniFactors)*
Lc (bufAeval) == bufAeval));
8557
8558 if (!derivXZero && !fail2 && !symmetric)
8559 {
8563 "time for univariate factorization in y over Fq: ");
8564 DEBOUTLN (cerr,
"Lc (bufAeval2)*prod (bufUniFactors2)== bufAeval2 " <<
8565 (
prod (bufUniFactors2)*
Lc (bufAeval2) == bufAeval2));
8566 }
8567
8568 if (bufUniFactors.
length() == 1 ||
8569 (!fail2 && !derivXZero && !symmetric && (bufUniFactors2.
length() == 1)))
8570 {
8571 if (extension)
8572 {
8575 }
8576 else
8578
8581
8582 if (!extension)
8584 delete [] bounds;
8585 delete [] bounds2;
8586 return factors;
8587 }
8588
8589 if (
i == 0 && !extension)
8590 {
8591 if (subCheck1 > 0)
8592 {
8594
8595 if (subCheck > 1 && (subCheck1%subCheck == 0))
8596 {
8598 subst (bufA, bufA, subCheck,
x);
8603 if (!extension)
8605 delete [] bounds;
8606 delete [] bounds2;
8607 return factors;
8608 }
8609 }
8610
8611 if (!derivXZero && !fail2 && !symmetric && subCheck2 > 0)
8612 {
8614
8615 if (subCheck > 1 && (subCheck2%subCheck == 0))
8616 {
8618 subst (bufA, bufA, subCheck,
y);
8623 if (!extension)
8625 delete [] bounds;
8626 delete [] bounds2;
8627 return factors;
8628 }
8629 }
8630 }
8631
8632
8634 if (!derivXZero && !fail2 && !symmetric)
8636
8638 {
8641 uniFactors= bufUniFactors;
8642 degs= bufDegs;
8643 if (!derivXZero && !fail2 && !symmetric)
8644 {
8645 Aeval2= bufAeval2;
8646 evaluation2= bufEvaluation2;
8647 uniFactors2= bufUniFactors2;
8648 degs2= bufDegs2;
8649 }
8650 }
8651 else
8652 {
8654 if (!derivXZero && !fail2 && !symmetric)
8655 {
8658 {
8659 uniFactors2= bufUniFactors2;
8660 Aeval2= bufAeval2;
8661 evaluation2= bufEvaluation2;
8662 }
8663 }
8665 {
8666 uniFactors= bufUniFactors;
8669 }
8670 }
8671 list.
append (bufEvaluation);
8672 if (!derivXZero && !fail2 && !symmetric)
8673 list2.
append (bufEvaluation2);
8674 }
8676 "total time for univariate factorizations: ");
8677
8678 if (!derivXZero && !fail2 && !symmetric)
8679 {
8680 if ((uniFactors.
length() > uniFactors2.
length() && minBound2 <= minBound)||
8683 {
8684 degs= degs2;
8685 uniFactors= uniFactors2;
8689 swap2= true;
8690 }
8691 }
8692
8694 {
8695 if (extension)
8696 {
8699 }
8700 else
8704 if (!extension)
8706 delete [] bounds;
8707 delete [] bounds2;
8708 return factors;
8709 }
8710
8712
8713 if (swap2)
8714 {
8715 delete [] bounds;
8716 bounds= bounds2;
8717 minBound= minBound2;
8718 }
8719
8723 "time to shift eval to zero: ");
8724
8725 int degMipo= 1;
8728
8729 DEBOUTLN (cerr,
"uniFactors= " << uniFactors);
8730
8731 if ((GF && !extension) || (GF && extension &&
k != 1))
8732 {
8733 bool earlySuccess= false;
8737 (
A, earlySuccess, earlyFactors, degs, liftBound,
8740 "time for bivariate hensel lifting over Fq: ");
8741 DEBOUTLN (cerr,
"lifted factors= " << uniFactors);
8742
8744
8746 if (extension)
8749 else
8753 "time for naive bivariate factor recombi over Fq: ");
8754
8755 if (earlySuccess)
8756 factors=
Union (earlyFactors, factors);
8757 else if (!earlySuccess && degs.
getLength() == 1)
8758 factors= earlyFactors;
8759 }
8761 {
8763 if (extension)
8764 {
8767 );
8768 factors=
Union (lll, factors);
8769 }
8771 {
8774 factors=
Union (lll, factors);
8775 }
8776 else if (!extension && (
alpha !=
x || GF))
8777 {
8780 factors=
Union (lll, factors);
8781 }
8783 "time to bivar lift and LLL recombi over Fq: ");
8784 DEBOUTLN (cerr,
"lifted factors= " << uniFactors);
8785 }
8786 else
8787 {
8788 bool earlySuccess= false;
8792 (
A, earlySuccess, earlyFactors, degs, liftBound,
8795 "time for bivar hensel lifting over Fq: ");
8796 DEBOUTLN (cerr,
"lifted factors= " << uniFactors);
8797
8799 if (!extension)
8800 {
8804 "time for small subset naive recombi over Fq: ");
8805
8806 int oldUniFactorsLength= uniFactors.
length();
8808 {
8814 );
8815 else
8816 {
8820 );
8821 else
8824 );
8825 }
8827 "time to increase precision: ");
8828 factors=
Union (factors, tmp);
8830 && uniFactors.
length() != oldUniFactorsLength)
8831 )
8832 {
8839 )
8840 );
8841 }
8842 }
8843 }
8844 else
8845 {
8847 {
8849 {
8852 );
8853 }
8854 else
8855 {
8858 );
8860 {
8868 )
8869 );
8870 }
8871 }
8872 }
8873 else
8874 {
8877 );
8878 int oldUniFactorsLength= uniFactors.
length();
8880 {
8881 int degMipo;
8883
8887 info2, source, dest, liftBound
8888 );
8889 factors=
Union (factors, tmp);
8891 && uniFactors.
length() != oldUniFactorsLength)
8892 )
8893 {
8900 )
8901 );
8902 }
8903 }
8904 }
8905 }
8906
8907 if (earlySuccess)
8908 factors=
Union (earlyFactors, factors);
8909 else if (!earlySuccess && degs.
getLength() == 1)
8910 factors= earlyFactors;
8911 }
8912
8913 if (!swap2)
8914 delete [] bounds2;
8915 delete [] bounds;
8916
8919 if (!extension)
8921
8922 return factors;
8923}
const CanonicalForm CFMap CFMap & N
CanonicalForm decompress(const CanonicalForm &F, const mpz_t *inverseM, const mpz_t *A)
decompress a bivariate poly
#define GaloisFieldDomain
CanonicalForm compress(const CanonicalForm &f, CFMap &m)
CanonicalForm compress ( const CanonicalForm & f, CFMap & m )
static CanonicalForm mapDown(const CanonicalForm &F, const Variable &alpha, const CanonicalForm &G, CFList &source, CFList &dest)
the CanonicalForm G is the output of map_up, returns F considered as an element over ,...
DegreePattern provides a functionality to create, intersect and refine degree patterns.
void intersect(const DegreePattern °Pat)
intersect two degree patterns
int getLength() const
getter
void refine()
Refine a degree pattern. Assumes that (*this)[0]:= d is the degree of the poly to be factored....
ExtensionInfo contains information about extension.
factory's class for variables
#define DEBOUTLN(stream, objects)
const CanonicalForm int const CFList & evaluation
const CanonicalForm int const CFList const Variable & y
CFFList append(const CFFList &Inputlist, const CFFactor &TheFactor)
CanonicalForm subst(const CanonicalForm &f, const CFList &a, const CFList &b, const CanonicalForm &Rstar, bool isFunctionField)
CFList *& Aeval
<[in] poly
int * computeBounds(const CanonicalForm &F, int &n, bool &isIrreducible)
compute bounds for logarithmic derivative as described in K. Belabas, M. van Hoeij,...
void appendSwapDecompress(CFList &factors1, const CFList &factors2, const CFList &factors3, const bool swap1, const bool swap2, const CFMap &N)
first swap Variables in factors1 if necessary, then append factors2 and factors3 on factors1 and fina...
void appendMapDown(CFList &factors, const CanonicalForm &g, const ExtensionInfo &info, CFList &source, CFList &dest)
map g down into a subfield of the current field and append it to factors
CanonicalForm reverseSubst(const CanonicalForm &F, const int d, const Variable &x)
reverse a substitution x^d->x
int substituteCheck(const CanonicalForm &F, const Variable &x)
check if a substitution x^n->x is possible
int * computeBoundsWrtDiffMainvar(const CanonicalForm &F, int &n, bool &isIrreducible)
as above just wrt to the other variable
CFList biFactorize(const CanonicalForm &F, const ExtensionInfo &info)
bivariate factorization over finite fields as decribed in "Factoring multivariate polynomials over a ...
CFList increasePrecision(CanonicalForm &F, CFList &factors, int factorsFound, int oldNumCols, int oldL, int precision, const CanonicalForm &eval)
CFList extHenselLiftAndLatticeRecombi(const CanonicalForm &G, const CFList &uniFactors, const ExtensionInfo &extInfo, const DegreePattern °Pat, const CanonicalForm &eval)
CFList extBiFactorize(const CanonicalForm &F, const ExtensionInfo &info)
Factorization over an extension of initial field.
CFList increasePrecisionFq2Fp(CanonicalForm &F, CFList &factors, int factorsFound, int oldNumCols, int oldL, const Variable &alpha, int precision, const CanonicalForm &eval)
CFList extIncreasePrecision(CanonicalForm &F, CFList &factors, int factorsFound, int oldNumCols, int oldL, const CanonicalForm &evaluation, const ExtensionInfo &info, CFList &source, CFList &dest, int precision)
CFList henselLiftAndLatticeRecombi(const CanonicalForm &G, const CFList &uniFactors, const Variable &alpha, const DegreePattern °Pat, bool symmetric, const CanonicalForm &eval)
CFList extFactorRecombination(CFList &factors, CanonicalForm &F, const CanonicalForm &N, const ExtensionInfo &info, DegreePattern °s, const CanonicalForm &eval, int s, int thres)
naive factor recombination as decribed in "Factoring multivariate polynomials over a finite field" by...
CanonicalForm evalPoint(const CanonicalForm &F, CanonicalForm &eval, const Variable &alpha, CFList &list, const bool &GF, bool &fail)
find an evaluation point p, s.t. F(p,y) is squarefree and .
CFList henselLiftAndEarly(CanonicalForm &A, bool &earlySuccess, CFList &earlyFactors, DegreePattern °s, int &liftBound, const CFList &uniFactors, const ExtensionInfo &info, const CanonicalForm &eval, modpk &b, CanonicalForm &den)
hensel Lifting and early factor detection
CFList uniFactorizer(const CanonicalForm &A, const Variable &alpha, const bool &GF)
Univariate factorization of squarefree monic polys over finite fields via NTL. If the characteristic ...
CFList factorRecombination(CFList &factors, CanonicalForm &F, const CanonicalForm &N, DegreePattern °s, const CanonicalForm &eval, int s, int thres, const modpk &b, const CanonicalForm &den)
naive factor recombination as decribed in "Factoring multivariate polynomials over a finite field" by...
ExtensionInfo init4ext(const ExtensionInfo &info, const CanonicalForm &evaluation, int °Mipo)
CFList increasePrecision2(const CanonicalForm &F, CFList &factors, const Variable &alpha, int precision)
template CanonicalForm tmin(const CanonicalForm &, const CanonicalForm &)
template List< Variable > Union(const List< Variable > &, const List< Variable > &)
bool isIrreducible(const CanonicalForm &f)
bool isIrreducible ( const CanonicalForm & f )
bool delta(X x, Y y, D d)
int status int void * buf
static poly normalize(poly next_p, ideal add_generators, syStrategy syzstr, int *g_l, int *p_l, int crit_comp)
#define TIMING_END_AND_PRINT(t, msg)
CanonicalForm getMipo(const Variable &alpha, const Variable &x)