cf_algorithm.h File Reference

declarations of higher level algorithms. More...

#include "canonicalform.h"
#include "variable.h"

Go to the source code of this file.

Functions
CanonicalForm	psr (const CanonicalForm &f, const CanonicalForm &g, const Variable &x)
	CanonicalForm psr ( const CanonicalForm & f, const CanonicalForm & g, const Variable & x ) More...
CanonicalForm	psq (const CanonicalForm &f, const CanonicalForm &g, const Variable &x)
	CanonicalForm psq ( const CanonicalForm & f, const CanonicalForm & g, const Variable & x ) More...
void	psqr (const CanonicalForm &f, const CanonicalForm &g, CanonicalForm &q, CanonicalForm &r, const Variable &x)
	void psqr ( const CanonicalForm & f, const CanonicalForm & g, CanonicalForm & q, CanonicalForm & r, const Variable & x ) More...
CanonicalForm FACTORY_PUBLIC	bCommonDen (const CanonicalForm &f)
	CanonicalForm bCommonDen ( const CanonicalForm & f ) More...
bool	fdivides (const CanonicalForm &f, const CanonicalForm &g)
	bool fdivides ( const CanonicalForm & f, const CanonicalForm & g ) More...
bool	fdivides (const CanonicalForm &f, const CanonicalForm &g, CanonicalForm &quot)
	same as fdivides if true returns quotient quot of g by f otherwise quot == 0 More...
bool	tryFdivides (const CanonicalForm &f, const CanonicalForm &g, const CanonicalForm &M, bool &fail)
	same as fdivides but handles zero divisors in Z_p[t]/(f)[x1,...,xn] for reducible f More...
CanonicalForm	maxNorm (const CanonicalForm &f)
	CanonicalForm maxNorm ( const CanonicalForm & f ) More...
CanonicalForm	euclideanNorm (const CanonicalForm &f)
	CanonicalForm euclideanNorm ( const CanonicalForm & f ) More...
void FACTORY_PUBLIC	chineseRemainder (const CanonicalForm &x1, const CanonicalForm &q1, const CanonicalForm &x2, const CanonicalForm &q2, CanonicalForm &xnew, CanonicalForm &qnew)
	void chineseRemainder ( const CanonicalForm & x1, const CanonicalForm & q1, const CanonicalForm & x2, const CanonicalForm & q2, CanonicalForm & xnew, CanonicalForm & qnew ) More...
void FACTORY_PUBLIC	chineseRemainder (const CFArray &x, const CFArray &q, CanonicalForm &xnew, CanonicalForm &qnew)
	void chineseRemainder ( const CFArray & x, const CFArray & q, CanonicalForm & xnew, CanonicalForm & qnew ) More...
void FACTORY_PUBLIC	chineseRemainderCached (const CanonicalForm &x1, const CanonicalForm &q1, const CanonicalForm &x2, const CanonicalForm &q2, CanonicalForm &xnew, CanonicalForm &qnew, CFArray &inv)
void FACTORY_PUBLIC	chineseRemainderCached (const CFArray &a, const CFArray &n, CanonicalForm &xnew, CanonicalForm &prod, CFArray &inv)
CanonicalForm	Farey (const CanonicalForm &f, const CanonicalForm &q)
	Farey rational reconstruction. More...
bool	isPurePoly (const CanonicalForm &f)
bool	isPurePoly_m (const CanonicalForm &f)
CFFList FACTORY_PUBLIC	factorize (const CanonicalForm &f, bool issqrfree=false)
	factorization over or More...
CFFList FACTORY_PUBLIC	factorize (const CanonicalForm &f, const Variable &alpha)
	factorization over or More...
CFFList FACTORY_PUBLIC	sqrFree (const CanonicalForm &f, bool sort=false)
	squarefree factorization More...
CanonicalForm	homogenize (const CanonicalForm &f, const Variable &x)
	homogenize homogenizes f with Variable x More...
CanonicalForm	homogenize (const CanonicalForm &f, const Variable &x, const Variable &v1, const Variable &v2)
Variable	get_max_degree_Variable (const CanonicalForm &f)
	get_max_degree_Variable returns Variable with highest degree. More...
CFList	get_Terms (const CanonicalForm &f)
void	getTerms (const CanonicalForm &f, const CanonicalForm &t, CFList &result)
	get_Terms: Split the polynomial in the containing terms. More...
bool	linearSystemSolve (CFMatrix &M)
CanonicalForm FACTORY_PUBLIC	determinant (const CFMatrix &M, int n)
CFArray	subResChain (const CanonicalForm &f, const CanonicalForm &g, const Variable &x)
	CFArray subResChain ( const CanonicalForm & f, const CanonicalForm & g, const Variable & x ) More...
CanonicalForm FACTORY_PUBLIC	resultant (const CanonicalForm &f, const CanonicalForm &g, const Variable &x)
	CanonicalForm resultant ( const CanonicalForm & f, const CanonicalForm & g, const Variable & x ) More...
CanonicalForm	abs (const CanonicalForm &f)
	inline CanonicalForm abs ( const CanonicalForm & f ) More...

Variables
EXTERN_VAR int	singular_homog_flag

Detailed Description

declarations of higher level algorithms.

Header file corresponds to: cf_algorithm.cc, cf_chinese.cc, cf_factor.cc, cf_linsys.cc, cf_resultant.cc

Hierarchy: mathematical algorithms on canonical forms

Developers note:

This header file collects declarations of most of the functions in Factory which implement higher level algorithms on canonical forms (factorization, gcd, etc.) and declarations of some low level mathematical functions, too (absolute value, euclidean norm, etc.).

Definition in file cf_algorithm.h.

Function Documentation

abs()

CanonicalForm abs ( const CanonicalForm &  f )

inline

inline CanonicalForm abs ( const CanonicalForm & f )

abs() - return absolute value of ‘f’.

The absolute value is defined in terms of the function ‘sign()’. If it reports negative sign for ‘f’ than -‘f’ is returned, otherwise ‘f’.

This behaviour is most useful for integers and rationals. But it may be used to sign-normalize the leading coefficient of arbitrary polynomials, too.

Type info:

f: CurrentPP

Definition at line 117 of file cf_algorithm.h.

{
    // it is not only more general to use `sign()' instead of a
    // direct comparison `f < 0', it is faster, too
    if ( sign( f ) < 0 )
        return -f;
    else
        return f;
}

bCommonDen()

CanonicalForm FACTORY_PUBLIC bCommonDen

(

const CanonicalForm &

f

)

CanonicalForm bCommonDen ( const CanonicalForm & f )

bCommonDen() - calculate multivariate common denominator of coefficients of ‘f’.

The common denominator is calculated with respect to all coefficients of ‘f’ which are in a base domain. In other words, common_den( ‘f’ ) * ‘f’ is guaranteed to have integer coefficients only. The common denominator of zero is one.

Returns something non-trivial iff the current domain is Q.

Type info:

f: CurrentPP

Definition at line 293 of file cf_algorithm.cc.

{
    if ( getCharacteristic() == 0 && isOn( SW_RATIONAL ) )
    {
        // otherwise `bgcd()' returns one
        Off( SW_RATIONAL );
        CanonicalForm result = internalBCommonDen( f );
        On( SW_RATIONAL );
        return result;
    }
    else
        return CanonicalForm( 1 );
}

chineseRemainder() [1/2]

void FACTORY_PUBLIC chineseRemainder	(	const CanonicalForm &	x1,
		const CanonicalForm &	q1,
		const CanonicalForm &	x2,
		const CanonicalForm &	q2,
		CanonicalForm &	xnew,
		CanonicalForm &	qnew
	)

void chineseRemainder ( const CanonicalForm & x1, const CanonicalForm & q1, const CanonicalForm & x2, const CanonicalForm & q2, CanonicalForm & xnew, CanonicalForm & qnew )

chineseRemainder - integer chinese remaindering.

Calculate xnew such that xnew=x1 (mod q1) and xnew=x2 (mod q2) and qnew = q1*q2. q1 and q2 should be positive integers, pairwise prime, x1 and x2 should be polynomials with integer coefficients. If x1 and x2 are polynomials with positive coefficients, the result is guaranteed to have positive coefficients, too.

Note: This algorithm is optimized for the case q1>>q2.

This is a standard algorithm. See, for example, Geddes/Czapor/Labahn - 'Algorithms for Computer Algebra', par. 5.6 and 5.8, or the article of M. Lauer - 'Computing by Homomorphic Images' in B. Buchberger - 'Computer Algebra - Symbolic and Algebraic Computation'.

Note: Be sure you are calculating in Z, and not in Q!

Definition at line 57 of file cf_chinese.cc.

{
    DEBINCLEVEL( cerr, "chineseRemainder" );
 
    DEBOUTLN( cerr, "log(q1) = " << q1.ilog2() );
    DEBOUTLN( cerr, "log(q2) = " << q2.ilog2() );
 
    // We calculate xnew as follows:
    //     xnew = v1 + v2 * q1
    // where
    //     v1 = x1 (mod q1)
    //     v2 = (x2-v1)/q1 (mod q2)  (*)
    //
    // We do one extra test to check whether x2-v1 vanishes (mod
    // q2) in (*) since it is not costly and may save us
    // from calculating the inverse of q1 (mod q2).
    //
    // u: v1 (mod q2)
    // d: x2-v1 (mod q2)
    // s: 1/q1 (mod q2)
    //
    CanonicalForm v2, v1;
    CanonicalForm u, d, s, dummy;
 
    v1 = mod( x1, q1 );
    u = mod( v1, q2 );
    d = mod( x2-u, q2 );
    if ( d.isZero() )
    {
        xnew = v1;
        qnew = q1 * q2;
        DEBDECLEVEL( cerr, "chineseRemainder" );
        return;
    }
    (void)bextgcd( q1, q2, s, dummy );
    v2 = mod( d*s, q2 );
    xnew = v1 + v2*q1;
 
    // After all, calculate new modulus.  It is important that
    // this is done at the very end of the algorithm, since q1
    // and qnew may refer to the same object (same is true for x1
    // and xnew).
    qnew = q1 * q2;
 
    DEBDECLEVEL( cerr, "chineseRemainder" );
}

chineseRemainder() [2/2]

void FACTORY_PUBLIC chineseRemainder	(	const CFArray &	x,
		const CFArray &	q,
		CanonicalForm &	xnew,
		CanonicalForm &	qnew
	)

void chineseRemainder ( const CFArray & x, const CFArray & q, CanonicalForm & xnew, CanonicalForm & qnew )

chineseRemainder - integer chinese remaindering.

Calculate xnew such that xnew=x[i] (mod q[i]) and qnew is the product of all q[i]. q[i] should be positive integers, pairwise prime. x[i] should be polynomials with integer coefficients. If all coefficients of all x[i] are positive integers, the result is guaranteed to have positive coefficients, too.

This is a standard algorithm, too, except for the fact that we use a divide-and-conquer method instead of a linear approach to calculate the remainder.

Note: Be sure you are calculating in Z, and not in Q!

Definition at line 124 of file cf_chinese.cc.

{
    DEBINCLEVEL( cerr, "chineseRemainder( ... CFArray ... )" );
 
    ASSERT( x.min() == q.min() && x.size() == q.size(), "incompatible arrays" );
    CFArray X(x), Q(q);
    int i, j, n = x.size(), start = x.min();
 
    DEBOUTLN( cerr, "array size = " << n );
 
    while ( n != 1 )
    {
        i = j = start;
        while ( i < start + n - 1 )
        {
            // This is a little bit dangerous: X[i] and X[j] (and
            // Q[i] and Q[j]) may refer to the same object.  But
            // xnew and qnew in the above function are modified
            // at the very end of the function, so we do not
            // modify x1 and q1, resp., by accident.
            chineseRemainder( X[i], Q[i], X[i+1], Q[i+1], X[j], Q[j] );
            i += 2;
            j++;
        }
 
        if ( n & 1 )
        {
            X[j] = X[i];
            Q[j] = Q[i];
        }
        // Maybe we would get some memory back at this point if
        // we would set X[j+1, ..., n] and Q[j+1, ..., n] to zero
        // at this point?
 
        n = ( n + 1) / 2;
    }
    xnew = X[start];
    qnew = Q[q.min()];
 
    DEBDECLEVEL( cerr, "chineseRemainder( ... CFArray ... )" );
}

chineseRemainderCached() [1/2]

void FACTORY_PUBLIC chineseRemainderCached	(	const CanonicalForm &	x1,
		const CanonicalForm &	q1,
		const CanonicalForm &	x2,
		const CanonicalForm &	q2,
		CanonicalForm &	xnew,
		CanonicalForm &	qnew,
		CFArray &	inv
	)

Definition at line 308 of file cf_chinese.cc.

{
  CFArray A(2); A[0]=a; A[1]=b;
  CFArray Q(2); Q[0]=q1; Q[1]=q2;
  chineseRemainderCached(A,Q,xnew,qnew,inv);
}

chineseRemainderCached() [2/2]

void FACTORY_PUBLIC chineseRemainderCached	(	const CFArray &	a,
		const CFArray &	n,
		CanonicalForm &	xnew,
		CanonicalForm &	prod,
		CFArray &	inv
	)

Definition at line 290 of file cf_chinese.cc.

{
  CanonicalForm p, sum=0L; prod=1L;
  int i;
  int len=n.size();
 
  for (i = 0; i < len; i++) prod *= n[i];
 
  for (i = 0; i < len; i++)
  {
    p = prod / n[i];
    sum += a[i] * chin_mul_inv(p, n[i], i, inv) * p;
  }
 
  xnew = mod(sum , prod);
}

determinant()

CanonicalForm FACTORY_PUBLIC determinant	(	const CFMatrix &	M,
		int	n
	)

Definition at line 222 of file cf_linsys.cc.

{
    typedef int* int_ptr;
 
    ASSERT( rows <= M.rows() && rows <= M.columns() && rows > 0, "undefined determinant" );
    if ( rows == 1 )
        return M(1,1);
    else  if ( rows == 2 )
        return M(1,1)*M(2,2)-M(2,1)*M(1,2);
    else  if ( matrix_in_Z( M, rows ) )
    {
        int ** mm = new int_ptr[rows];
        CanonicalForm x, q, Qhalf, B;
        int n, i, intdet, p, pno;
        for ( i = 0; i < rows; i++ )
        {
            mm[i] = new int[rows];
        }
        pno = 0; n = 0;
        TIMING_START(det_bound);
        B = detbound( M, rows );
        TIMING_END(det_bound);
        q = 1;
        TIMING_START(det_numprimes);
        while ( B > q && n < cf_getNumBigPrimes() )
        {
            q *= cf_getBigPrime( n );
            n++;
        }
        TIMING_END(det_numprimes);
 
        CFArray X(1,n), Q(1,n);
 
        while ( pno < n )
        {
            p = cf_getBigPrime( pno );
            setCharacteristic( p );
            // map matrix into char p
            TIMING_START(det_mapping);
            fill_int_mat( M, mm, rows );
            TIMING_END(det_mapping);
            pno++;
            DEBOUT( cerr, "." );
            TIMING_START(det_determinant);
            intdet = determinant( mm, rows );
            TIMING_END(det_determinant);
            setCharacteristic( 0 );
            X[pno] = intdet;
            Q[pno] = p;
        }
        TIMING_START(det_chinese);
        chineseRemainder( X, Q, x, q );
        TIMING_END(det_chinese);
        Qhalf = q / 2;
        if ( x > Qhalf )
            x = x - q;
        for ( i = 0; i < rows; i++ )
            delete [] mm[i];
        delete [] mm;
        return x;
    }
    else
    {
        CFMatrix m( M );
        CanonicalForm divisor = 1, pivot, mji;
        int i, j, k, sign = 1;
        for ( i = 1; i <= rows; i++ ) {
            pivot = m(i,i); k = i;
            for ( j = i+1; j <= rows; j++ ) {
                if ( betterpivot( pivot, m(j,i) ) ) {
                    pivot = m(j,i);
                    k = j;
                }
            }
            if ( pivot.isZero() )
                return 0;
            if ( i != k )
            {
                m.swapRow( i, k );
                sign = -sign;
            }
            for ( j = i+1; j <= rows; j++ )
            {
                if ( ! m(j,i).isZero() )
                {
                    divisor *= pivot;
                    mji = m(j,i);
                    m(j,i) = 0;
                    for ( k = i+1; k <= rows; k++ )
                        m(j,k) = m(j,k) * pivot - m(i,k)*mji;
                }
            }
        }
        pivot = sign;
        for ( i = 1; i <= rows; i++ )
            pivot *= m(i,i);
        return pivot / divisor;
    }
}

euclideanNorm()

CanonicalForm euclideanNorm

(

const CanonicalForm &

f

)

CanonicalForm euclideanNorm ( const CanonicalForm & f )

euclideanNorm() - return Euclidean norm of ‘f’.

Returns the largest integer smaller or equal norm(‘f’) = sqrt(sum( ‘f’[i]^2 )).

Type info:

f: UVPoly( Z )

Definition at line 565 of file cf_algorithm.cc.

{
    ASSERT( (f.inBaseDomain() || f.isUnivariate()) && f.LC().inZ(),
            "type error: univariate poly over Z expected" );
 
    CanonicalForm result = 0;
    for ( CFIterator i = f; i.hasTerms(); i++ ) {
        CanonicalForm coeff = i.coeff();
        result += coeff*coeff;
    }
    return sqrt( result );
}

factorize() [1/2]

CFFList FACTORY_PUBLIC factorize	(	const CanonicalForm &	f,
		bool	issqrfree = false
	)

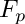
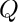
factorization over or

Definition at line 405 of file cf_factor.cc.

{
  if ( f.inCoeffDomain() )
        return CFFList( f );
#ifndef NOASSERT
  Variable a;
  ASSERT (!hasFirstAlgVar (f, a), "f has an algebraic variable use factorize \
          ( const CanonicalForm & f, const Variable & alpha ) instead");
#endif
  //out_cf("factorize:",f,"==================================\n");
  if (! f.isUnivariate() ) // preprocess homog. polys
  {
    if ( singular_homog_flag && f.isHomogeneous())
    {
      Variable xn = get_max_degree_Variable(f);
      int d_xn = degree(f,xn);
      CFMap n;
      CanonicalForm F = compress(f(1,xn),n);
      CFFList Intermediatelist;
      Intermediatelist = factorize(F);
      CFFList Homoglist;
      CFFListIterator j;
      for ( j=Intermediatelist; j.hasItem(); j++ )
      {
        Homoglist.append(
            CFFactor( n(j.getItem().factor()), j.getItem().exp()) );
      }
      CFFList Unhomoglist;
      CanonicalForm unhomogelem;
      for ( j=Homoglist; j.hasItem(); j++ )
      {
        unhomogelem= homogenize(j.getItem().factor(),xn);
        Unhomoglist.append(CFFactor(unhomogelem,j.getItem().exp()));
        d_xn -= (degree(unhomogelem,xn)*j.getItem().exp());
      }
      if ( d_xn != 0 ) // have to append xn^(d_xn)
        Unhomoglist.append(CFFactor(CanonicalForm(xn),d_xn));
      if(isOn(SW_USE_NTL_SORT)) Unhomoglist.sort(cmpCF);
      return Unhomoglist;
    }
  }
  CFFList F;
  if ( getCharacteristic() > 0 )
  {
    if (f.isUnivariate())
    {
#ifdef HAVE_FLINT
#ifdef HAVE_NTL
      if (degree (f) < 300)
#endif
      {
        // use FLINT: char p, univariate
        nmod_poly_t f1;
        convertFacCF2nmod_poly_t (f1, f);
        nmod_poly_factor_t result;
        nmod_poly_factor_init (result);
        mp_limb_t leadingCoeff= nmod_poly_factor (result, f1);
        F= convertFLINTnmod_poly_factor2FacCFFList (result, leadingCoeff, f.mvar());
        nmod_poly_factor_clear (result);
        nmod_poly_clear (f1);
        if(isOn(SW_USE_NTL_SORT)) F.sort(cmpCF);
        return F;
      }
#endif
#ifdef HAVE_NTL
      { // NTL char 2, univariate
        if (getCharacteristic()==2)
        {
          // Specialcase characteristic==2
          if (fac_NTL_char != 2)
          {
            fac_NTL_char = 2;
            zz_p::init(2);
          }
          // convert to NTL using the faster conversion routine for characteristic 2
          GF2X f1=convertFacCF2NTLGF2X(f);
          // no make monic necessary in GF2
          //factorize
          vec_pair_GF2X_long factors;
          CanZass(factors,f1);
 
          // convert back to factory again using the faster conversion routine for vectors over GF2X
          F=convertNTLvec_pair_GF2X_long2FacCFFList(factors,LeadCoeff(f1),f.mvar());
          if(isOn(SW_USE_NTL_SORT)) F.sort(cmpCF);
          return F;
        }
      }
#endif
#ifdef HAVE_NTL
      {
        // use NTL char p, univariate
        if (fac_NTL_char != getCharacteristic())
        {
          fac_NTL_char = getCharacteristic();
          zz_p::init(getCharacteristic());
        }
 
        // convert to NTL
        zz_pX f1=convertFacCF2NTLzzpX(f);
        zz_p leadcoeff = LeadCoeff(f1);
 
        //make monic
        f1=f1 / LeadCoeff(f1);
        // factorize
        vec_pair_zz_pX_long factors;
        CanZass(factors,f1);
 
        F=convertNTLvec_pair_zzpX_long2FacCFFList(factors,leadcoeff,f.mvar());
        //test_cff(F,f);
        if(isOn(SW_USE_NTL_SORT)) F.sort(cmpCF);
        return F;
      }
#endif
#if !defined(HAVE_NTL) && !defined(HAVE_FLINT)
      // Use Factory without NTL and without FLINT: char p, univariate
      {
        if ( isOn( SW_BERLEKAMP ) )
          F=FpFactorizeUnivariateB( f, issqrfree );
        else
          F=FpFactorizeUnivariateCZ( f, issqrfree, 0, Variable(), Variable() );
        return F;
      }
#endif
    }
    else // char p, multivariate
    {
      if (CFFactory::gettype() == GaloisFieldDomain)
      {
        #if defined(HAVE_NTL)
        if (issqrfree)
        {
          CFList factors;
          Variable alpha;
          factors= GFSqrfFactorize (f);
          for (CFListIterator i= factors; i.hasItem(); i++)
            F.append (CFFactor (i.getItem(), 1));
        }
        else
        {
          Variable alpha;
          F= GFFactorize (f);
        }
        #else
        factoryError ("multivariate factorization over GF depends on NTL(missing)");
        return CFFList (CFFactor (f, 1));
        #endif
      }
      else
      {
        #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20700) && defined(HAVE_NTL)
        if (!isOn(SW_USE_FL_FAC_P))
        {
        #endif
        #if defined(HAVE_NTL)
          if (issqrfree)
          {
            CFList factors;
            Variable alpha;
            factors= FpSqrfFactorize (f);
            for (CFListIterator i= factors; i.hasItem(); i++)
              F.append (CFFactor (i.getItem(), 1));
            goto end_charp;
          }
          else
          {
            Variable alpha;
            F= FpFactorize (f);
            goto end_charp;
          }
        #endif
        #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20700) && defined(HAVE_NTL)
        }
        #endif
        #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20700)
        nmod_mpoly_ctx_t ctx;
        nmod_mpoly_ctx_init(ctx,f.level(),ORD_LEX,getCharacteristic());
        nmod_mpoly_t Flint_f;
        nmod_mpoly_init(Flint_f,ctx);
        convFactoryPFlintMP(f,Flint_f,ctx,f.level());
        nmod_mpoly_factor_t factors;
        nmod_mpoly_factor_init(factors,ctx);
        int okay;
        if (issqrfree) okay=nmod_mpoly_factor_squarefree(factors,Flint_f,ctx);
        else           okay=nmod_mpoly_factor(factors,Flint_f,ctx);
        nmod_mpoly_t fac;
        nmod_mpoly_init(fac,ctx);
        CanonicalForm cf_fac;
        int cf_exp;
        cf_fac=nmod_mpoly_factor_get_constant_ui(factors,ctx);
        F.append(CFFactor(cf_fac,1));
        for(int i=nmod_mpoly_factor_length(factors,ctx)-1; i>=0; i--)
        {
          nmod_mpoly_factor_get_base(fac,factors,i,ctx);
          cf_fac=convFlintMPFactoryP(fac,ctx,f.level());
          cf_exp=nmod_mpoly_factor_get_exp_si(factors,i,ctx);
          F.append(CFFactor(cf_fac,cf_exp));
        }
        nmod_mpoly_factor_clear(factors,ctx);
        nmod_mpoly_clear(Flint_f,ctx);
        nmod_mpoly_ctx_clear(ctx);
        if (okay==0)
        {
          Off(SW_USE_FL_GCD_P);
          Off(SW_USE_FL_FAC_P);
          F=factorize(f,issqrfree);
          On(SW_USE_FL_GCD_P);
          On(SW_USE_FL_FAC_P);
        }
        #endif
        #if !defined(HAVE_FLINT) || (__FLINT_RELEASE < 20700)
        #ifndef HAVE_NTL
        factoryError ("multivariate factorization depends on NTL/FLINT(missing)");
        return CFFList (CFFactor (f, 1));
        #endif
        #endif
      }
    }
  }
  else // char 0
  {
    bool on_rational = isOn(SW_RATIONAL);
    On(SW_RATIONAL);
    CanonicalForm cd = bCommonDen( f );
    CanonicalForm fz = f * cd;
    Off(SW_RATIONAL);
    if ( f.isUnivariate() )
    {
      CanonicalForm ic=icontent(fz);
      fz/=ic;
      if (fz.degree()==1)
      {
        F=CFFList(CFFactor(fz,1));
        F.insert(CFFactor(ic,1));
      }
      else
      #if defined(HAVE_FLINT) && (__FLINT_RELEASE>=20503)  && (__FLINT_RELEASE!= 20600)
      {
        // FLINT 2.6.0 has a bug:
        // factorize x^12-13*x^10-13*x^8+13*x^4+13*x^2-1 runs forever
        // use FLINT: char 0, univariate
        fmpz_poly_t f1;
        convertFacCF2Fmpz_poly_t (f1, fz);
        fmpz_poly_factor_t result;
        fmpz_poly_factor_init (result);
        fmpz_poly_factor(result, f1);
        F= convertFLINTfmpz_poly_factor2FacCFFList (result, fz.mvar());
        fmpz_poly_factor_clear (result);
        fmpz_poly_clear (f1);
        if ( ! ic.isOne() )
        {
           // according to convertFLINTfmpz_polyfactor2FcaCFFlist,
           //  first entry is in CoeffDomain
          CFFactor new_first( F.getFirst().factor() * ic );
          F.removeFirst();
          F.insert( new_first );
        }
      }
      goto end_char0;
      #elif defined(HAVE_NTL)
      {
        //use NTL
        ZZ c;
        vec_pair_ZZX_long factors;
        //factorize the converted polynomial
        factor(c,factors,convertFacCF2NTLZZX(fz));
 
        //convert the result back to Factory
        F=convertNTLvec_pair_ZZX_long2FacCFFList(factors,c,fz.mvar());
        if ( ! ic.isOne() )
        {
           // according to convertNTLvec_pair_ZZX_long2FacCFFList
           //  first entry is in CoeffDomain
          CFFactor new_first( F.getFirst().factor() * ic );
          F.removeFirst();
          F.insert( new_first );
        }
      }
      goto end_char0;
      #else
      {
        //Use Factory without NTL: char 0, univariate
        F = ZFactorizeUnivariate( fz, issqrfree );
        goto end_char0;
      }
      #endif
    }
    else // multivariate,  char 0
    {
      #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20700)
      if (isOn(SW_USE_FL_FAC_0))
      {
        On (SW_RATIONAL);
        fmpz_mpoly_ctx_t ctx;
        fmpz_mpoly_ctx_init(ctx,f.level(),ORD_LEX);
        fmpz_mpoly_t Flint_f;
        fmpz_mpoly_init(Flint_f,ctx);
        convFactoryPFlintMP(fz,Flint_f,ctx,fz.level());
        fmpz_mpoly_factor_t factors;
        fmpz_mpoly_factor_init(factors,ctx);
        int rr;
        if (issqrfree) rr=fmpz_mpoly_factor_squarefree(factors,Flint_f,ctx);
        else           rr=fmpz_mpoly_factor(factors,Flint_f,ctx);
        if (rr==0) printf("fail\n");
        fmpz_mpoly_t fac;
        fmpz_mpoly_init(fac,ctx);
        CanonicalForm cf_fac;
        int cf_exp;
        fmpz_t c;
        fmpz_init(c);
        fmpz_mpoly_factor_get_constant_fmpz(c,factors,ctx);
        cf_fac=convertFmpz2CF(c);
        fmpz_clear(c);
        F.append(CFFactor(cf_fac,1));
        for(int i=fmpz_mpoly_factor_length(factors,ctx)-1; i>=0; i--)
        {
           fmpz_mpoly_factor_get_base(fac,factors,i,ctx);
           cf_fac=convFlintMPFactoryP(fac,ctx,f.level());
           cf_exp=fmpz_mpoly_factor_get_exp_si(factors,i,ctx);
           F.append(CFFactor(cf_fac,cf_exp));
        }
        fmpz_mpoly_factor_clear(factors,ctx);
        fmpz_mpoly_clear(Flint_f,ctx);
        fmpz_mpoly_ctx_clear(ctx);
        goto end_char0;
      }
      #endif
      #if defined(HAVE_NTL)
      On (SW_RATIONAL);
      if (issqrfree)
      {
        CFList factors= ratSqrfFactorize (fz);
        for (CFListIterator i= factors; i.hasItem(); i++)
          F.append (CFFactor (i.getItem(), 1));
      }
      else
      {
        F = ratFactorize (fz);
      }
      #endif
      #if !defined(HAVE_FLINT) || (__FLINT_RELEASE < 20700)
      #ifndef HAVE_NTL
      F=ZFactorizeMultivariate(fz, issqrfree);
      #endif
      #endif
    }
 
end_char0:
    if ( on_rational )
      On(SW_RATIONAL);
    else
      Off(SW_RATIONAL);
    if ( ! cd.isOne() )
    {
      CFFactor new_first( F.getFirst().factor() / cd );
      F.removeFirst();
      F.insert( new_first );
    }
  }
 
#if defined(HAVE_NTL)
end_charp:
#endif
  if(isOn(SW_USE_NTL_SORT)) F.sort(cmpCF);
  return F;
}

factorize() [2/2]

CFFList FACTORY_PUBLIC factorize	(	const CanonicalForm &	f,
		const Variable &	alpha
	)

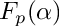
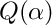
factorization over or

Definition at line 774 of file cf_factor.cc.

{
  if ( f.inCoeffDomain() )
    return CFFList( f );
  //out_cf("factorize:",f,"==================================\n");
  //out_cf("mipo:",getMipo(alpha),"\n");
 
  CFFList F;
  ASSERT( alpha.level() < 0 && getReduce (alpha), "not an algebraic extension" );
#ifndef NOASSERT
  Variable beta;
  if (hasFirstAlgVar(f, beta))
    ASSERT (beta == alpha, "f has an algebraic variable that \
                            does not coincide with alpha");
#endif
  int ch=getCharacteristic();
  if (ch>0)
  {
    if (f.isUnivariate())
    {
#ifdef HAVE_NTL
      if (/*getCharacteristic()*/ch==2)
      {
        // special case : GF2
 
        // remainder is two ==> nothing to do
 
        // set minimal polynomial in NTL using the optimized conversion routines for characteristic 2
        GF2X minPo=convertFacCF2NTLGF2X(getMipo(alpha,f.mvar()));
        GF2E::init (minPo);
 
        // convert to NTL again using the faster conversion routines
        GF2EX f1;
        if (isPurePoly(f))
        {
          GF2X f_tmp=convertFacCF2NTLGF2X(f);
          f1=to_GF2EX(f_tmp);
        }
        else
          f1=convertFacCF2NTLGF2EX(f,minPo);
 
        // make monic (in Z/2(a))
        GF2E f1_coef=LeadCoeff(f1);
        MakeMonic(f1);
 
        // factorize using NTL
        vec_pair_GF2EX_long factors;
        CanZass(factors,f1);
 
        // return converted result
        F=convertNTLvec_pair_GF2EX_long2FacCFFList(factors,f1_coef,f.mvar(),alpha);
        if(isOn(SW_USE_NTL_SORT)) F.sort(cmpCF);
        return F;
      }
#endif
#if (HAVE_FLINT && __FLINT_RELEASE >= 20400)
      {
        // use FLINT
        nmod_poly_t FLINTmipo, leadingCoeff;
        fq_nmod_ctx_t fq_con;
 
        nmod_poly_init (FLINTmipo, ch);
        nmod_poly_init (leadingCoeff, ch);
        convertFacCF2nmod_poly_t (FLINTmipo, getMipo (alpha));
 
        fq_nmod_ctx_init_modulus (fq_con, FLINTmipo, "Z");
        fq_nmod_poly_t FLINTF;
        convertFacCF2Fq_nmod_poly_t (FLINTF, f, fq_con);
        fq_nmod_poly_factor_t res;
        fq_nmod_poly_factor_init (res, fq_con);
        fq_nmod_poly_factor (res, leadingCoeff, FLINTF, fq_con);
        F= convertFLINTFq_nmod_poly_factor2FacCFFList (res, f.mvar(), alpha, fq_con);
        F.insert (CFFactor (Lc (f), 1));
 
        fq_nmod_poly_factor_clear (res, fq_con);
        fq_nmod_poly_clear (FLINTF, fq_con);
        nmod_poly_clear (FLINTmipo);
        nmod_poly_clear (leadingCoeff);
        fq_nmod_ctx_clear (fq_con);
        if(isOn(SW_USE_NTL_SORT)) F.sort(cmpCF);
        return F;
      }
#endif
#ifdef HAVE_NTL
      {
        // use NTL
        if (fac_NTL_char != ch)
        {
          fac_NTL_char = ch;
          zz_p::init(ch);
        }
 
        // set minimal polynomial in NTL
        zz_pX minPo=convertFacCF2NTLzzpX(getMipo(alpha));
        zz_pE::init (minPo);
 
        // convert to NTL
        zz_pEX f1=convertFacCF2NTLzz_pEX(f,minPo);
        zz_pE leadcoeff= LeadCoeff(f1);
 
        //make monic
        f1=f1 / leadcoeff; //leadcoeff==LeadCoeff(f1);
 
        // factorize
        vec_pair_zz_pEX_long factors;
        CanZass(factors,f1);
 
        // return converted result
        F=convertNTLvec_pair_zzpEX_long2FacCFFList(factors,leadcoeff,f.mvar(),alpha);
        //test_cff(F,f);
        if(isOn(SW_USE_NTL_SORT)) F.sort(cmpCF);
        return F;
      }
#endif
#if !defined(HAVE_NTL) && !defined(HAVE_FLINT)
      // char p, extension, univariate
      CanonicalForm c=Lc(f);
      CanonicalForm fc=f/c;
      F=FpFactorizeUnivariateCZ( fc, false, 1, alpha, Variable() );
      F.insert (CFFactor (c, 1));
#endif
    }
    else // char p, multivariate
    {
      #if (HAVE_FLINT && __FLINT_RELEASE >= 20700)
        // use FLINT
        nmod_poly_t FLINTmipo;
        fq_nmod_ctx_t fq_con;
        fq_nmod_mpoly_ctx_t ctx;
 
        nmod_poly_init (FLINTmipo, ch);
        convertFacCF2nmod_poly_t (FLINTmipo, getMipo (alpha));
 
        fq_nmod_ctx_init_modulus (fq_con, FLINTmipo, "Z");
        fq_nmod_mpoly_ctx_init(ctx,f.level(),ORD_LEX,fq_con);
 
        fq_nmod_mpoly_t FLINTF;
        fq_nmod_mpoly_init(FLINTF,ctx);
        convertFacCF2Fq_nmod_mpoly_t(FLINTF,f,ctx,f.level(),fq_con);
        fq_nmod_mpoly_factor_t res;
        fq_nmod_mpoly_factor_init (res, ctx);
        fq_nmod_mpoly_factor (res, FLINTF, ctx);
        F= convertFLINTFq_nmod_mpoly_factor2FacCFFList (res, ctx,f.level(),fq_con,alpha);
        //F.insert (CFFactor (Lc (f), 1));
 
        fq_nmod_mpoly_factor_clear (res, ctx);
        fq_nmod_mpoly_clear (FLINTF, ctx);
        nmod_poly_clear (FLINTmipo);
        fq_nmod_mpoly_ctx_clear (ctx);
        fq_nmod_ctx_clear (fq_con);
        if(isOn(SW_USE_NTL_SORT)) F.sort(cmpCF);
        return F;
      #elif defined(HAVE_NTL)
      F= FqFactorize (f, alpha);
      #else
      factoryError ("multivariate factorization over Z/pZ(alpha) depends on NTL/Flint(missing)");
      return CFFList (CFFactor (f, 1));
      #endif
    }
  }
  else // Q(a)[x]
  {
    if (f.isUnivariate())
    {
      F= AlgExtFactorize (f, alpha);
    }
    else //Q(a)[x1,...,xn]
    {
      #if defined(HAVE_NTL) || defined(HAVE_FLINT)
      F= ratFactorize (f, alpha);
      #else
      factoryError ("multivariate factorization over Q(alpha) depends on NTL or FLINT (missing)");
      return CFFList (CFFactor (f, 1));
      #endif
    }
  }
  if(isOn(SW_USE_NTL_SORT)) F.sort(cmpCF);
  return F;
}

Farey()

CanonicalForm Farey	(	const CanonicalForm &	f,
		const CanonicalForm &	q
	)

Farey rational reconstruction.

If NTL is available it uses the fast algorithm from NTL, i.e. Encarnacion, Collins.

Definition at line 202 of file cf_chinese.cc.

{
  int is_rat=isOn(SW_RATIONAL);
  Off(SW_RATIONAL);
  Variable x = f.mvar();
  CanonicalForm result = 0;
  CanonicalForm c;
  CFIterator i;
#ifdef HAVE_FLINT
  fmpz_t FLINTq;
  fmpz_init(FLINTq);
  convertCF2initFmpz(FLINTq,q);
  fmpz_t FLINTc;
  fmpz_init(FLINTc);
  fmpq_t FLINTres;
  fmpq_init(FLINTres);
#elif defined(HAVE_NTL)
  ZZ NTLq= convertFacCF2NTLZZ (q);
  ZZ bound;
  SqrRoot (bound, NTLq/2);
#else
  factoryError("NTL/FLINT missing:Farey");
#endif
  for ( i = f; i.hasTerms(); i++ )
  {
    c = i.coeff();
    if ( c.inCoeffDomain())
    {
#ifdef HAVE_FLINT
      if (c.inZ())
      {
        convertCF2initFmpz(FLINTc,c);
        fmpq_reconstruct_fmpz(FLINTres,FLINTc,FLINTq);
        result += power (x, i.exp())*(convertFmpq2CF(FLINTres));
      }
#elif defined(HAVE_NTL)
      if (c.inZ())
      {
        ZZ NTLc= convertFacCF2NTLZZ (c);
        bool lessZero= (sign (NTLc) == -1);
        if (lessZero)
          NTL::negate (NTLc, NTLc);
        ZZ NTLnum, NTLden;
        if (ReconstructRational (NTLnum, NTLden, NTLc, NTLq, bound, bound))
        {
          if (lessZero)
            NTL::negate (NTLnum, NTLnum);
          CanonicalForm num= convertNTLZZX2CF (to_ZZX (NTLnum), Variable (1));
          CanonicalForm den= convertNTLZZX2CF (to_ZZX (NTLden), Variable (1));
          On (SW_RATIONAL);
          result += power (x, i.exp())*(num/den);
          Off (SW_RATIONAL);
        }
      }
#else
      if (c.inZ())
        result += power (x, i.exp()) * Farey_n(c,q);
#endif
      else
        result += power( x, i.exp() ) * Farey(c,q);
    }
    else
      result += power( x, i.exp() ) * Farey(c,q);
  }
  if (is_rat) On(SW_RATIONAL);
#ifdef HAVE_FLINT
  fmpq_clear(FLINTres);
  fmpz_clear(FLINTc);
  fmpz_clear(FLINTq);
#endif
  return result;
}

fdivides() [1/2]

bool fdivides	(	const CanonicalForm &	f,
		const CanonicalForm &	g
	)

bool fdivides ( const CanonicalForm & f, const CanonicalForm & g )

fdivides() - check whether ‘f’ divides ‘g’.

Returns true iff ‘f’ divides ‘g’. Uses some extra heuristic to avoid polynomial division. Without the heuristic, the test essentialy looks like ‘divremt(g, f, q, r) && r.isZero()’.

Type info:

f, g: Current

Elements from prime power domains (or polynomials over such domains) are admissible if ‘f’ (or lc(‘f’), resp.) is not a zero divisor. This is a slightly stronger precondition than mathematically necessary since divisibility is a well-defined notion in arbitrary rings. Hence, we decided not to declare the weaker type ‘CurrentPP’.

Developers note:

One may consider the the test ‘fdivides( f.LC(), g.LC() )’ in the main ‘if’-test superfluous since ‘divremt()’ in the ‘if’-body repeats the test. However, ‘divremt()’ does not use any heuristic to do so.

It seems not reasonable to call ‘fdivides()’ from ‘divremt()’ to check divisibility of leading coefficients. ‘fdivides()’ is on a relatively high level compared to ‘divremt()’.

Definition at line 340 of file cf_algorithm.cc.

{
    // trivial cases
    if ( g.isZero() )
        return true;
    else if ( f.isZero() )
        return false;
 
    if ( (f.inCoeffDomain() || g.inCoeffDomain())
         && ((getCharacteristic() == 0 && isOn( SW_RATIONAL ))
             || (getCharacteristic() > 0) ))
    {
        // if we are in a field all elements not equal to zero are units
        if ( f.inCoeffDomain() )
            return true;
        else
            // g.inCoeffDomain()
            return false;
    }
 
    // we may assume now that both levels either equal LEVELBASE
    // or are greater zero
    int fLevel = f.level();
    int gLevel = g.level();
    if ( (gLevel > 0) && (fLevel == gLevel) )
        // f and g are polynomials in the same main variable
        if ( degree( f ) <= degree( g )
             && fdivides( f.tailcoeff(), g.tailcoeff() )
             && fdivides( f.LC(), g.LC() ) )
        {
            CanonicalForm q, r;
            return divremt( g, f, q, r ) && r.isZero();
        }
        else
            return false;
    else if ( gLevel < fLevel )
        // g is a coefficient w.r.t. f
        return false;
    else
    {
        // either f is a coefficient w.r.t. polynomial g or both
        // f and g are from a base domain (should be Z or Z/p^n,
        // then)
        CanonicalForm q, r;
        return divremt( g, f, q, r ) && r.isZero();
    }
}

fdivides() [2/2]

bool fdivides	(	const CanonicalForm &	f,
		const CanonicalForm &	g,
		CanonicalForm &	quot
	)

same as fdivides if true returns quotient quot of g by f otherwise quot == 0

Definition at line 390 of file cf_algorithm.cc.

{
    quot= 0;
    // trivial cases
    if ( g.isZero() )
        return true;
    else if ( f.isZero() )
        return false;
 
    if ( (f.inCoeffDomain() || g.inCoeffDomain())
         && ((getCharacteristic() == 0 && isOn( SW_RATIONAL ))
             || (getCharacteristic() > 0) ))
    {
        // if we are in a field all elements not equal to zero are units
        if ( f.inCoeffDomain() )
        {
            quot= g/f;
            return true;
        }
        else
            // g.inCoeffDomain()
            return false;
    }
 
    // we may assume now that both levels either equal LEVELBASE
    // or are greater zero
    int fLevel = f.level();
    int gLevel = g.level();
    if ( (gLevel > 0) && (fLevel == gLevel) )
        // f and g are polynomials in the same main variable
        if ( degree( f ) <= degree( g )
             && fdivides( f.tailcoeff(), g.tailcoeff() )
             && fdivides( f.LC(), g.LC() ) )
        {
            CanonicalForm q, r;
            if (divremt( g, f, q, r ) && r.isZero())
            {
              quot= q;
              return true;
            }
            else
              return false;
        }
        else
            return false;
    else if ( gLevel < fLevel )
        // g is a coefficient w.r.t. f
        return false;
    else
    {
        // either f is a coefficient w.r.t. polynomial g or both
        // f and g are from a base domain (should be Z or Z/p^n,
        // then)
        CanonicalForm q, r;
        if (divremt( g, f, q, r ) && r.isZero())
        {
          quot= q;
          return true;
        }
        else
          return false;
    }
}

get_max_degree_Variable()

Variable get_max_degree_Variable

(

const CanonicalForm &

f

)

get_max_degree_Variable returns Variable with highest degree.

We assume f is not a constant!

Definition at line 260 of file cf_factor.cc.

{
  ASSERT( ( ! f.inCoeffDomain() ), "no constants" );
  int max=0, maxlevel=0, n=level(f);
  for ( int i=1; i<=n; i++ )
  {
    if (degree(f,Variable(i)) >= max)
    {
      max= degree(f,Variable(i)); maxlevel= i;
    }
  }
  return Variable(maxlevel);
}

get_Terms()

CFList get_Terms

(

const CanonicalForm &

f

)

Definition at line 289 of file cf_factor.cc.

                                    {
  CFList result,dummy,dummy2;
  CFIterator i;
  CFListIterator j;
 
  if ( getNumVars(f) == 0 ) result.append(f);
  else{
    Variable _x(level(f));
    for ( i=f; i.hasTerms(); i++ ){
      getTerms(i.coeff(), 1, dummy);
      for ( j=dummy; j.hasItem(); j++ )
        result.append(j.getItem() * power(_x, i.exp()));
 
      dummy= dummy2; // have to initalize new
    }
  }
  return result;
}

getTerms()

void getTerms	(	const CanonicalForm &	f,
		const CanonicalForm &	t,
		CFList &	result
	)

get_Terms: Split the polynomial in the containing terms.

getTerms: the real work is done here.

Definition at line 279 of file cf_factor.cc.

{
  if ( getNumVars(f) == 0 ) result.append(f*t);
  else{
    Variable x(level(f));
    for ( CFIterator i=f; i.hasTerms(); i++ )
      getTerms( i.coeff(), t*power(x,i.exp()), result);
  }
}

homogenize() [1/2]

CanonicalForm homogenize	(	const CanonicalForm &	f,
		const Variable &	x
	)

homogenize homogenizes f with Variable x

Definition at line 313 of file cf_factor.cc.

{
#if 0
  int maxdeg=totaldegree(f), deg;
  CFIterator i;
  CanonicalForm elem, result(0);
 
  for (i=f; i.hasTerms(); i++)
  {
    elem= i.coeff()*power(f.mvar(),i.exp());
    deg = totaldegree(elem);
    if ( deg < maxdeg )
      result += elem * power(x,maxdeg-deg);
    else
      result+=elem;
  }
  return result;
#else
  CFList Newlist, Termlist= get_Terms(f);
  int maxdeg=totaldegree(f), deg;
  CFListIterator i;
  CanonicalForm elem, result(0);
 
  for (i=Termlist; i.hasItem(); i++)
  {
    elem= i.getItem();
    deg = totaldegree(elem);
    if ( deg < maxdeg )
      Newlist.append(elem * power(x,maxdeg-deg));
    else
      Newlist.append(elem);
  }
  for (i=Newlist; i.hasItem(); i++) // rebuild
    result += i.getItem();
 
  return result;
#endif
}

homogenize() [2/2]

CanonicalForm homogenize	(	const CanonicalForm &	f,
		const Variable &	x,
		const Variable &	v1,
		const Variable &	v2
	)

Definition at line 353 of file cf_factor.cc.

{
#if 0
  int maxdeg=totaldegree(f), deg;
  CFIterator i;
  CanonicalForm elem, result(0);
 
  for (i=f; i.hasTerms(); i++)
  {
    elem= i.coeff()*power(f.mvar(),i.exp());
    deg = totaldegree(elem);
    if ( deg < maxdeg )
      result += elem * power(x,maxdeg-deg);
    else
      result+=elem;
  }
  return result;
#else
  CFList Newlist, Termlist= get_Terms(f);
  int maxdeg=totaldegree(f), deg;
  CFListIterator i;
  CanonicalForm elem, result(0);
 
  for (i=Termlist; i.hasItem(); i++)
  {
    elem= i.getItem();
    deg = totaldegree(elem,v1,v2);
    if ( deg < maxdeg )
      Newlist.append(elem * power(x,maxdeg-deg));
    else
      Newlist.append(elem);
  }
  for (i=Newlist; i.hasItem(); i++) // rebuild
    result += i.getItem();
 
  return result;
#endif
}

isPurePoly()

bool isPurePoly

(

const CanonicalForm &

f

)

Definition at line 244 of file cf_factor.cc.

{
  if (f.level()<=0) return false;
  for (CFIterator i=f;i.hasTerms();i++)
  {
    if (!(i.coeff().inBaseDomain())) return false;
  }
  return true;
}

isPurePoly_m()

bool isPurePoly_m

(

const CanonicalForm &

f

)

Definition at line 234 of file cf_factor.cc.

{
  if (f.inBaseDomain()) return true;
  if (f.level()<0) return false;
  for (CFIterator i=f;i.hasTerms();i++)
  {
    if (!isPurePoly_m(i.coeff())) return false;
  }
  return true;
}

linearSystemSolve()

bool linearSystemSolve

(

CFMatrix &

M

)

Definition at line 78 of file cf_linsys.cc.

{
    typedef int* int_ptr;
 
    if ( ! matrix_in_Z( M ) ) {
        int nrows = M.rows(), ncols = M.columns();
        int i, j, k;
        CanonicalForm rowpivot, pivotrecip;
        // triangularization
        for ( i = 1; i <= nrows; i++ ) {
            //find "pivot"
            for (j = i; j <= nrows; j++ )
                if ( M(j,i) != 0 ) break;
            if ( j > nrows ) return false;
            if ( j != i )
                M.swapRow( i, j );
            pivotrecip = 1 / M(i,i);
            for ( j = 1; j <= ncols; j++ )
                M(i,j) *= pivotrecip;
            for ( j = i+1; j <= nrows; j++ ) {
                rowpivot = M(j,i);
                if ( rowpivot == 0 ) continue;
                for ( k = i; k <= ncols; k++ )
                    M(j,k) -= M(i,k) * rowpivot;
            }
        }
        // matrix is now upper triangular with 1s down the diagonal
        // back-substitute
        for ( i = nrows-1; i > 0; i-- ) {
            for ( j = nrows+1; j <= ncols; j++ ) {
                for ( k = i+1; k <= nrows; k++ )
                    M(i,j) -= M(k,j) * M(i,k);
            }
        }
        return true;
    }
    else {
        int rows = M.rows(), cols = M.columns();
        CFMatrix MM( rows, cols );
        int ** mm = new int_ptr[rows];
        CanonicalForm Q, Qhalf, mnew, qnew, B;
        int i, j, p, pno;
        bool ok;
 
        // initialize room to hold the result and the result mod p
        for ( i = 0; i < rows; i++ ) {
            mm[i] = new int[cols];
        }
 
        // calculate the bound for the result
        B = bound( M );
        DEBOUTLN( cerr, "bound = " <<  B );
 
        // find a first solution mod p
        pno = 0;
        do {
            DEBOUTSL( cerr );
            DEBOUT( cerr, "trying prime(" << pno << ") = " );
            p = cf_getBigPrime( pno );
            DEBOUT( cerr, p );
            DEBOUTENDL( cerr );
            setCharacteristic( p );
            // map matrix into char p
            for ( i = 1; i <= rows; i++ )
                for ( j = 1; j <= cols; j++ )
                    mm[i-1][j-1] = mapinto( M(i,j) ).intval();
            // solve mod p
            ok = solve( mm, rows, cols );
            pno++;
        } while ( ! ok );
 
        // initialize the result matrix with first solution
        setCharacteristic( 0 );
        for ( i = 1; i <= rows; i++ )
            for ( j = rows+1; j <= cols; j++ )
                MM(i,j) = mm[i-1][j-1];
 
        // Q so far
        Q = p;
        while ( Q < B && pno < cf_getNumBigPrimes() ) {
            do {
                DEBOUTSL( cerr );
                DEBOUT( cerr, "trying prime(" << pno << ") = " );
                p = cf_getBigPrime( pno );
                DEBOUT( cerr, p );
                DEBOUTENDL( cerr );
                setCharacteristic( p );
                for ( i = 1; i <= rows; i++ )
                    for ( j = 1; j <= cols; j++ )
                        mm[i-1][j-1] = mapinto( M(i,j) ).intval();
                // solve mod p
                ok = solve( mm, rows, cols );
                pno++;
            } while ( ! ok );
            // found a solution mod p
            // now chinese remainder it to a solution mod Q*p
            setCharacteristic( 0 );
            for ( i = 1; i <= rows; i++ )
                for ( j = rows+1; j <= cols; j++ )
                {
                    chineseRemainder( MM[i][j], Q, CanonicalForm(mm[i-1][j-1]), CanonicalForm(p), mnew, qnew );
                    MM(i, j) = mnew;
                }
            Q = qnew;
        }
        if ( pno == cf_getNumBigPrimes() )
            fuzzy_result = true;
        else
            fuzzy_result = false;
        // store the result in M
        Qhalf = Q / 2;
        for ( i = 1; i <= rows; i++ ) {
            for ( j = rows+1; j <= cols; j++ )
                if ( MM(i,j) > Qhalf )
                    M(i,j) = MM(i,j) - Q;
                else
                    M(i,j) = MM(i,j);
            delete [] mm[i-1];
        }
        delete [] mm;
        return ! fuzzy_result;
    }
}

maxNorm()

CanonicalForm maxNorm

(

const CanonicalForm &

f

)

CanonicalForm maxNorm ( const CanonicalForm & f )

maxNorm() - return maximum norm of ‘f’.

That is, the base coefficient of ‘f’ with the largest absolute value.

Valid for arbitrary polynomials over arbitrary domains, but most useful for multivariate polynomials over Z.

Type info:

f: CurrentPP

Definition at line 536 of file cf_algorithm.cc.

{
    if ( f.inBaseDomain() )
        return abs( f );
    else {
        CanonicalForm result = 0;
        for ( CFIterator i = f; i.hasTerms(); i++ ) {
            CanonicalForm coeffMaxNorm = maxNorm( i.coeff() );
            if ( coeffMaxNorm > result )
                result = coeffMaxNorm;
        }
        return result;
    }
}

psq()

CanonicalForm psq	(	const CanonicalForm &	f,
		const CanonicalForm &	g,
		const Variable &	x
	)

CanonicalForm psq ( const CanonicalForm & f, const CanonicalForm & g, const Variable & x )

psq() - return pseudo quotient of ‘f’ and ‘g’ with respect to ‘x’.

‘g’ must not equal zero.

Type info:

f, g: Current x: Polynomial

Developers note:

This is not an optimal implementation. Better would have been an implementation in ‘InternalPoly’ avoiding the exponentiation of the leading coefficient of ‘g’. It seemed not worth to do so.

See also

psr(), psqr()

Definition at line 172 of file cf_algorithm.cc.

{
    ASSERT( x.level() > 0, "type error: polynomial variable expected" );
    ASSERT( ! g.isZero(), "math error: division by zero" );
 
    // swap variables such that x's level is larger or equal
    // than both f's and g's levels.
    Variable X = tmax( tmax( f.mvar(), g.mvar() ), x );
    CanonicalForm F = swapvar( f, x, X );
    CanonicalForm G = swapvar( g, x, X );
 
    // now, we have to calculate the pseudo remainder of F and G
    // w.r.t. X
    int fDegree = degree( F, X );
    int gDegree = degree( G, X );
    if ( fDegree < 0 || fDegree < gDegree )
        return 0;
    else {
        CanonicalForm result = (power( LC( G, X ), fDegree-gDegree+1 ) * F) / G;
        return swapvar( result, x, X );
    }
}

psqr()

void psqr	(	const CanonicalForm &	f,
		const CanonicalForm &	g,
		CanonicalForm &	q,
		CanonicalForm &	r,
		const Variable &	x
	)

void psqr ( const CanonicalForm & f, const CanonicalForm & g, CanonicalForm & q, CanonicalForm & r, const Variable & x )

psqr() - calculate pseudo quotient and remainder of ‘f’ and ‘g’ with respect to ‘x’.

Returns the pseudo quotient of ‘f’ and ‘g’ in ‘q’, the pseudo remainder in ‘r’. ‘g’ must not equal zero.

See ‘psr()’ for more detailed information.

Type info:

f, g: Current q, r: Anything x: Polynomial

Developers note:

This is not an optimal implementation. Better would have been an implementation in ‘InternalPoly’ avoiding the exponentiation of the leading coefficient of ‘g’. It seemed not worth to do so.

See also

psr(), psq()

Definition at line 223 of file cf_algorithm.cc.

{
    ASSERT( x.level() > 0, "type error: polynomial variable expected" );
    ASSERT( ! g.isZero(), "math error: division by zero" );
 
    // swap variables such that x's level is larger or equal
    // than both f's and g's levels.
    Variable X = tmax( tmax( f.mvar(), g.mvar() ), x );
    CanonicalForm F = swapvar( f, x, X );
    CanonicalForm G = swapvar( g, x, X );
 
    // now, we have to calculate the pseudo remainder of F and G
    // w.r.t. X
    int fDegree = degree( F, X );
    int gDegree = degree( G, X );
    if ( fDegree < 0 || fDegree < gDegree ) {
        q = 0; r = f;
    } else {
        divrem( power( LC( G, X ), fDegree-gDegree+1 ) * F, G, q, r );
        q = swapvar( q, x, X );
        r = swapvar( r, x, X );
    }
}

psr()

CanonicalForm psr	(	const CanonicalForm &	rr,
		const CanonicalForm &	vv,
		const Variable &	x
	)

CanonicalForm psr ( const CanonicalForm & f, const CanonicalForm & g, const Variable & x )

psr() - return pseudo remainder of ‘f’ and ‘g’ with respect to ‘x’.

‘g’ must not equal zero.

For f and g in R[x], R an arbitrary ring, g != 0, there is a representation

LC(g)^s*f = g*q + r

with r = 0 or deg(r) < deg(g) and s = 0 if f = 0 or s = max( 0, deg(f)-deg(g)+1 ) otherwise. r = psr(f, g) and q = psq(f, g) are called "pseudo remainder" and "pseudo quotient", resp. They are uniquely determined if LC(g) is not a zero divisor in R.

See H.-J. Reiffen/G. Scheja/U. Vetter - "Algebra", 2nd ed., par. 15, for a reference.

Type info:

f, g: Current x: Polynomial

Polynomials over prime power domains are admissible if lc(LC(‘g’,‘x’)) is not a zero divisor. This is a slightly stronger precondition than mathematically necessary since pseudo remainder and quotient are well-defined if LC(‘g’,‘x’) is not a zero divisor.

For example, psr(y^2, (13*x+1)*y) is well-defined in (Z/13^2[x])[y] since (13*x+1) is not a zero divisor. But calculating it with Factory would fail since 13 is a zero divisor in Z/13^2.

Due to this inconsistency with mathematical notion, we decided not to declare type ‘CurrentPP’ for ‘f’ and ‘g’.

Developers note:

This is not an optimal implementation. Better would have been an implementation in ‘InternalPoly’ avoiding the exponentiation of the leading coefficient of ‘g’. In contrast to ‘psq()’ and ‘psqr()’ it definitely seems worth to implement the pseudo remainder on the internal level.

See also

psq(), psqr()

Definition at line 117 of file cf_algorithm.cc.

{
  CanonicalForm r=rr, v=vv, l, test, lu, lv, t, retvalue;
  int dr, dv, d,n=0;
 
 
  dr = degree( r, x );
  if (dr>0)
  {
    dv = degree( v, x );
    if (dv <= dr) {l=LC(v,x); v = v -l*power(x,dv);}
    else { l = 1; }
    d= dr-dv+1;
    //out_cf("psr(",rr," ");
    //out_cf("",vv," ");
    //printf(" var=%d\n",x.level());
    while ( ( dv <= dr  ) && ( !r.isZero()) )
    {
      test = power(x,dr-dv)*v*LC(r,x);
      if ( dr == 0 ) { r= CanonicalForm(0); }
      else { r= r - LC(r,x)*power(x,dr); }
      r= l*r -test;
      dr= degree(r,x);
      n+=1;
    }
    r= power(l, d-n)*r;
  }
  return r;
}

resultant()

CanonicalForm FACTORY_PUBLIC resultant	(	const CanonicalForm &	f,
		const CanonicalForm &	g,
		const Variable &	x
	)

CanonicalForm resultant ( const CanonicalForm & f, const CanonicalForm & g, const Variable & x )

resultant() - return resultant of f and g with respect to x.

The chain is calculated from f and g with respect to variable x which should not be an algebraic variable. If f or q equals zero, zero is returned. If f is a coefficient with respect to x, f^degree(g, x) is returned, analogously for g.

This algorithm serves as a wrapper around other resultant algorithms which do the real work. Here we use standard properties of resultants only.

Definition at line 173 of file cf_resultant.cc.

{
    ASSERT( x.level() > 0, "cannot calculate resultant with respect to algebraic variables" );
 
    // some checks on triviality.  We will not use degree( v )
    // here because this may involve variable swapping.
    if ( f.isZero() || g.isZero() )
        return 0;
    if ( f.mvar() < x )
        return power( f, g.degree( x ) );
    if ( g.mvar() < x )
        return power( g, f.degree( x ) );
 
    // make x main variale
    CanonicalForm F, G;
    Variable X;
    if ( f.mvar() > x || g.mvar() > x ) {
        if ( f.mvar() > g.mvar() )
            X = f.mvar();
        else
            X = g.mvar();
        F = swapvar( f, X, x );
        G = swapvar( g, X, x );
    }
    else {
        X = x;
        F = f;
        G = g;
    }
    // at this point, we have to calculate resultant( F, G, X )
    // where X is equal to or greater than the main variables
    // of F and G
 
    int m = degree( F, X );
    int n = degree( G, X );
    // catch trivial cases
    if ( m+n <= 2 || m == 0 || n == 0 )
        return swapvar( trivialResultant( F, G, X ), X, x );
 
    // exchange F and G if necessary
    int flipFactor;
    if ( m < n ) {
        CanonicalForm swap = F;
        F = G; G = swap;
        int degswap = m;
        m = n; n = degswap;
        if ( m & 1 && n & 1 )
            flipFactor = -1;
        else
            flipFactor = 1;
    } else
        flipFactor = 1;
 
    // this is not an effective way to calculate the resultant!
    CanonicalForm extFactor;
    if ( m == n ) {
        if ( n & 1 )
            extFactor = -LC( G, X );
        else
            extFactor = LC( G, X );
    } else
        extFactor = power( LC( F, X ), m-n-1 );
 
    CanonicalForm result;
    result = subResChain( F, G, X )[0] / extFactor;
 
    return swapvar( result, X, x ) * flipFactor;
}

sqrFree()

CFFList FACTORY_PUBLIC sqrFree	(	const CanonicalForm &	f,
		bool	sort = false
	)

squarefree factorization

Definition at line 957 of file cf_factor.cc.

{
//    ASSERT( f.isUnivariate(), "multivariate factorization not implemented" );
    CFFList result;
 
    if ( getCharacteristic() == 0 )
        result = sqrFreeZ( f );
    else
    {
        Variable alpha;
        if (hasFirstAlgVar (f, alpha))
          result = FqSqrf( f, alpha );
        else
          result= FpSqrf (f);
    }
    if (sort)
    {
      CFFactor buf= result.getFirst();
      result.removeFirst();
      result= sortCFFList (result);
      result.insert (buf);
    }
    return result;
}

subResChain()

CFArray subResChain	(	const CanonicalForm &	f,
		const CanonicalForm &	g,
		const Variable &	x
	)

CFArray subResChain ( const CanonicalForm & f, const CanonicalForm & g, const Variable & x )

subResChain() - caculate extended subresultant chain.

The chain is calculated from f and g with respect to variable x which should not be an algebraic variable. If f or q equals zero, an array consisting of one zero entry is returned.

Note: this is not the standard subresultant chain but the extended chain!

This algorithm is from the article of R. Loos - 'Generalized Polynomial Remainder Sequences' in B. Buchberger - 'Computer Algebra - Symbolic and Algebraic Computation' with some necessary extensions concerning the calculation of the first step.

Definition at line 42 of file cf_resultant.cc.

{
    ASSERT( x.level() > 0, "cannot calculate subresultant sequence with respect to algebraic variables" );
 
    CFArray trivialResult( 0, 0 );
    CanonicalForm F, G;
    Variable X;
 
    // some checks on triviality
    if ( f.isZero() || g.isZero() ) {
        trivialResult[0] = 0;
        return trivialResult;
    }
 
    // make x main variable
    if ( f.mvar() > x || g.mvar() > x ) {
        if ( f.mvar() > g.mvar() )
            X = f.mvar();
        else
            X = g.mvar();
        F = swapvar( f, X, x );
        G = swapvar( g, X, x );
    }
    else {
        X = x;
        F = f;
        G = g;
    }
    // at this point, we have to calculate the sequence of F and
    // G in respect to X where X is equal to or greater than the
    // main variables of F and G
 
    // initialization of chain
    int m = degree( F, X );
    int n = degree( G, X );
 
    int j = (m <= n) ? n : m-1;
    int r;
 
    CFArray S( 0, j+1 );
    CanonicalForm R;
    S[j+1] = F; S[j] = G;
 
    // make sure that S[j+1] is regular and j < n
    if ( m == n && j > 0 ) {
        S[j-1] = LC( S[j], X ) * psr( S[j+1], S[j], X );
        j--;
    } else if ( m < n ) {
        S[j-1] = LC( S[j], X ) * LC( S[j], X ) * S[j+1];
        j--;
    } else if ( m > n && j > 0 ) {
        // calculate first step
        r = degree( S[j], X );
        R = LC( S[j+1], X );
 
        // if there was a gap calculate similar polynomial
        if ( j > r && r >= 0 )
            S[r] = power( LC( S[j], X ), j - r ) * S[j] * power( R, j - r );
 
        if ( r > 0 ) {
            // calculate remainder
            S[r-1] = psr( S[j+1], S[j], X ) * power( -R, j - r );
            j = r-1;
        }
    }
 
    while ( j > 0 ) {
        // at this point, 0 < j < n and S[j+1] is regular
        r = degree( S[j], X );
        R = LC( S[j+1], X );
 
        // if there was a gap calculate similar polynomial
        if ( j > r && r >= 0 )
            S[r] = (power( LC( S[j], X ), j - r ) * S[j]) / power( R, j - r );
 
        if ( r <= 0 ) break;
        // calculate remainder
        S[r-1] = psr( S[j+1], S[j], X ) / power( -R, j - r + 2 );
 
        j = r-1;
        // again 0 <= j < r <= jOld and S[j+1] is regular
    }
 
    for ( j = 0; j <= S.max(); j++ ) {
        // reswap variables if necessary
        if ( X != x ) {
            S[j] = swapvar( S[j], X, x );
        }
    }
 
    return S;
}

tryFdivides()

bool tryFdivides	(	const CanonicalForm &	f,
		const CanonicalForm &	g,
		const CanonicalForm &	M,
		bool &	fail
	)

same as fdivides but handles zero divisors in Z_p[t]/(f)[x1,...,xn] for reducible f

Definition at line 456 of file cf_algorithm.cc.

{
    fail= false;
    // trivial cases
    if ( g.isZero() )
        return true;
    else if ( f.isZero() )
        return false;
 
    if (f.inCoeffDomain() || g.inCoeffDomain())
    {
        // if we are in a field all elements not equal to zero are units
        if ( f.inCoeffDomain() )
        {
            CanonicalForm inv;
            tryInvert (f, M, inv, fail);
            return !fail;
        }
        else
        {
            return false;
        }
    }
 
    // we may assume now that both levels either equal LEVELBASE
    // or are greater zero
    int fLevel = f.level();
    int gLevel = g.level();
    if ( (gLevel > 0) && (fLevel == gLevel) )
    {
        if (degree( f ) > degree( g ))
          return false;
        bool dividestail= tryFdivides (f.tailcoeff(), g.tailcoeff(), M, fail);
 
        if (fail || !dividestail)
          return false;
        bool dividesLC= tryFdivides (f.LC(),g.LC(), M, fail);
        if (fail || !dividesLC)
          return false;
        CanonicalForm q,r;
        bool divides= tryDivremt (g, f, q, r, M, fail);
        if (fail || !divides)
          return false;
        return r.isZero();
    }
    else if ( gLevel < fLevel )
    {
        // g is a coefficient w.r.t. f
        return false;
    }
    else
    {
        // either f is a coefficient w.r.t. polynomial g or both
        // f and g are from a base domain (should be Z or Z/p^n,
        // then)
        CanonicalForm q, r;
        bool divides= tryDivremt (g, f, q, r, M, fail);
        if (fail || !divides)
          return false;
        return r.isZero();
    }
}

Variable Documentation

singular_homog_flag

EXTERN_VAR int singular_homog_flag

Definition at line 65 of file cf_algorithm.h.