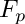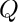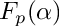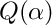406{
407 if (
f.inCoeffDomain() )
409#ifndef NOASSERT
412 ( const CanonicalForm & f, const Variable & alpha ) instead");
413#endif
414
415 if (!
f.isUnivariate() )
416 {
418 {
427 for (
j=Intermediatelist;
j.hasItem();
j++ )
428 {
430 CFFactor( n(
j.getItem().factor()),
j.getItem().exp()) );
431 }
434 for (
j=Homoglist;
j.hasItem();
j++ )
435 {
438 d_xn -= (
degree(unhomogelem,
xn)*
j.getItem().exp());
439 }
440 if ( d_xn != 0 )
443 return Unhomoglist;
444 }
445 }
448 {
449 if (
f.isUnivariate())
450 {
451#ifdef HAVE_FLINT
452#ifdef HAVE_NTL
454#endif
455 {
456
457 nmod_poly_t f1;
459 nmod_poly_factor_t
result;
460 nmod_poly_factor_init (
result);
461 mp_limb_t leadingCoeff= nmod_poly_factor (
result, f1);
463 nmod_poly_factor_clear (
result);
466 return F;
467 }
468#endif
469#ifdef HAVE_NTL
470 {
472 {
473
475 {
477 zz_p::init(2);
478 }
479
481
482
483 vec_pair_GF2X_long factors;
484 CanZass(factors,f1);
485
486
489 return F;
490 }
491 }
492#endif
493#ifdef HAVE_NTL
494 {
495
497 {
500 }
501
502
504 zz_p leadcoeff = LeadCoeff(f1);
505
506
507 f1=f1 / LeadCoeff(f1);
508
509 vec_pair_zz_pX_long factors;
510 CanZass(factors,f1);
511
513
515 return F;
516 }
517#endif
518#if !defined(HAVE_NTL) && !defined(HAVE_FLINT)
519
520 {
523 else
525 return F;
526 }
527#endif
528 }
529 else
530 {
532 {
533 #if defined(HAVE_NTL)
534 if (issqrfree)
535 {
541 }
542 else
543 {
546 }
547 #else
548 factoryError (
"multivariate factorization over GF depends on NTL(missing)");
550 #endif
551 }
552 else
553 {
554 #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20700) && defined(HAVE_NTL)
556 {
557 #endif
558 #if defined(HAVE_NTL)
559 if (issqrfree)
560 {
566 goto end_charp;
567 }
568 else
569 {
572 goto end_charp;
573 }
574 #endif
575 #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20700) && defined(HAVE_NTL)
576 }
577 #endif
578 #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20700)
579 nmod_mpoly_ctx_t ctx;
581 nmod_mpoly_t Flint_f;
582 nmod_mpoly_init(Flint_f,ctx);
583 convFactoryPFlintMP(
f,Flint_f,ctx,
f.level());
584 nmod_mpoly_factor_t factors;
585 nmod_mpoly_factor_init(factors,ctx);
586 int okay;
587 if (issqrfree) okay=nmod_mpoly_factor_squarefree(factors,Flint_f,ctx);
588 else okay=nmod_mpoly_factor(factors,Flint_f,ctx);
589 nmod_mpoly_t fac;
590 nmod_mpoly_init(fac,ctx);
592 int cf_exp;
593 cf_fac=nmod_mpoly_factor_get_constant_ui(factors,ctx);
595 for(
int i=nmod_mpoly_factor_length(factors,ctx)-1;
i>=0;
i--)
596 {
597 nmod_mpoly_factor_get_base(fac,factors,
i,ctx);
598 cf_fac=convFlintMPFactoryP(fac,ctx,
f.level());
599 cf_exp=nmod_mpoly_factor_get_exp_si(factors,
i,ctx);
601 }
602 nmod_mpoly_factor_clear(factors,ctx);
603 nmod_mpoly_clear(Flint_f,ctx);
604 nmod_mpoly_ctx_clear(ctx);
605 if (okay==0)
606 {
612 }
613 #endif
614 #if !defined(HAVE_FLINT) || (__FLINT_RELEASE < 20700)
615 #ifndef HAVE_NTL
616 factoryError (
"multivariate factorization depends on NTL/FLINT(missing)");
618 #endif
619 #endif
620 }
621 }
622 }
623 else
624 {
630 if (
f.isUnivariate() )
631 {
633 fz/=ic;
635 {
638 }
639 else
640 #if defined(HAVE_FLINT) && (__FLINT_RELEASE>=20503) && (__FLINT_RELEASE!= 20600)
641 {
642
643
644
645 fmpz_poly_t f1;
647 fmpz_poly_factor_t
result;
648 fmpz_poly_factor_init (
result);
649 fmpz_poly_factor(
result, f1);
651 fmpz_poly_factor_clear (
result);
652 fmpz_poly_clear (f1);
654 {
655
656
660 }
661 }
662 goto end_char0;
663 #elif defined(HAVE_NTL)
664 {
665
666 ZZ c;
667 vec_pair_ZZX_long factors;
668
670
671
674 {
675
676
680 }
681 }
682 goto end_char0;
683 #else
684 {
685
687 goto end_char0;
688 }
689 #endif
690 }
691 else
692 {
693 #if defined(HAVE_FLINT) && (__FLINT_RELEASE >= 20700)
695 {
697 fmpz_mpoly_ctx_t ctx;
698 fmpz_mpoly_ctx_init(ctx,
f.level(),ORD_LEX);
699 fmpz_mpoly_t Flint_f;
700 fmpz_mpoly_init(Flint_f,ctx);
701 convFactoryPFlintMP(fz,Flint_f,ctx,fz.
level());
702 fmpz_mpoly_factor_t factors;
703 fmpz_mpoly_factor_init(factors,ctx);
704 int rr;
705 if (issqrfree) rr=fmpz_mpoly_factor_squarefree(factors,Flint_f,ctx);
706 else rr=fmpz_mpoly_factor(factors,Flint_f,ctx);
707 if (rr==0) printf("fail\n");
708 fmpz_mpoly_t fac;
709 fmpz_mpoly_init(fac,ctx);
711 int cf_exp;
712 fmpz_t c;
713 fmpz_init(c);
714 fmpz_mpoly_factor_get_constant_fmpz(c,factors,ctx);
716 fmpz_clear(c);
718 for(
int i=fmpz_mpoly_factor_length(factors,ctx)-1;
i>=0;
i--)
719 {
720 fmpz_mpoly_factor_get_base(fac,factors,
i,ctx);
721 cf_fac=convFlintMPFactoryP(fac,ctx,
f.level());
722 cf_exp=fmpz_mpoly_factor_get_exp_si(factors,
i,ctx);
724 }
725 fmpz_mpoly_factor_clear(factors,ctx);
726 fmpz_mpoly_clear(Flint_f,ctx);
727 fmpz_mpoly_ctx_clear(ctx);
728 goto end_char0;
729 }
730 #endif
731 #if defined(HAVE_NTL)
733 if (issqrfree)
734 {
738 }
739 else
740 {
742 }
743 #endif
744 #if !defined(HAVE_FLINT) || (__FLINT_RELEASE < 20700)
745 #ifndef HAVE_NTL
747 #endif
748 #endif
749 }
750
751end_char0:
752 if ( on_rational )
754 else
757 {
761 }
762 }
763
764#if defined(HAVE_NTL)
765end_charp:
766#endif
768 return F;
769}
CanonicalForm convertFmpz2CF(const fmpz_t coefficient)
conversion of a FLINT integer to CanonicalForm
CFFList convertFLINTnmod_poly_factor2FacCFFList(const nmod_poly_factor_t fac, const mp_limb_t leadingCoeff, const Variable &x)
conversion of a FLINT factorization over Z/p (for word size p) to a CFFList
void convertFacCF2Fmpz_poly_t(fmpz_poly_t result, const CanonicalForm &f)
conversion of a factory univariate polynomial over Z to a fmpz_poly_t
CFFList convertFLINTfmpz_poly_factor2FacCFFList(const fmpz_poly_factor_t fac, const Variable &x)
conversion of a FLINT factorization over Z to a CFFList
CFFList convertNTLvec_pair_GF2X_long2FacCFFList(const vec_pair_GF2X_long &e, GF2, const Variable &x)
NAME: convertNTLvec_pair_GF2X_long2FacCFFList.
ZZX convertFacCF2NTLZZX(const CanonicalForm &f)
CFFList convertNTLvec_pair_zzpX_long2FacCFFList(const vec_pair_zz_pX_long &e, const zz_p cont, const Variable &x)
zz_pX convertFacCF2NTLzzpX(const CanonicalForm &f)
GF2X convertFacCF2NTLGF2X(const CanonicalForm &f)
NAME: convertFacCF2NTLGF2X.
CFFList convertNTLvec_pair_ZZX_long2FacCFFList(const vec_pair_ZZX_long &e, const ZZ &cont, const Variable &x)
NAME: convertNTLvec_pair_ZZX_long2FacCFFList.
CanonicalForm cd(bCommonDen(FF))
CanonicalForm bCommonDen(const CanonicalForm &f)
CanonicalForm bCommonDen ( const CanonicalForm & f )
#define ASSERT(expression, message)
static const int SW_USE_FL_GCD_P
set to 1 to use Flints gcd over F_p
static const int SW_RATIONAL
set to 1 for computations over Q
static const int SW_USE_NTL_SORT
set to 1 to sort factors in a factorization
static const int SW_USE_FL_FAC_0
set to 1 to prefer flints multivariate factorization over Z/p
static const int SW_USE_FL_FAC_P
set to 1 to prefer flints multivariate factorization over Z/p
static const int SW_BERLEKAMP
set to 1 to use Factorys Berlekamp alg.
#define GaloisFieldDomain
Variable get_max_degree_Variable(const CanonicalForm &f)
get_max_degree_Variable returns Variable with highest degree.
int cmpCF(const CFFactor &f, const CFFactor &g)
VAR int singular_homog_flag
CanonicalForm homogenize(const CanonicalForm &f, const Variable &x)
homogenize homogenizes f with Variable x
CFFList factorize(const CanonicalForm &f, bool issqrfree)
factorization over or
CanonicalForm compress(const CanonicalForm &f, CFMap &m)
CanonicalForm compress ( const CanonicalForm & f, CFMap & m )
VAR void(* factoryError)(const char *s)
void sort(int(*)(const T &, const T &))
factory's class for variables
CFFList ratFactorize(const CanonicalForm &G, const Variable &v=Variable(1), bool substCheck=true)
factorize a multivariate polynomial over
CFList ratSqrfFactorize(const CanonicalForm &G, const Variable &v=Variable(1))
factorize a squarefree multivariate polynomial over
CFList FpSqrfFactorize(const CanonicalForm &F)
factorize a squarefree multivariate polynomial over
CFFList FpFactorize(const CanonicalForm &G, bool substCheck=true)
factorize a multivariate polynomial over
CFFList GFFactorize(const CanonicalForm &G, bool substCheck=true)
factorize a multivariate polynomial over GF
CFList GFSqrfFactorize(const CanonicalForm &F)
factorize a squarefree multivariate polynomial over GF
convertFacCF2nmod_poly_t(FLINTmipo, M)
nmod_poly_clear(FLINTmipo)
CFFList FpFactorizeUnivariateB(const CanonicalForm &f, bool issqrfree=false)
CFFList FpFactorizeUnivariateCZ(const CanonicalForm &f, bool issqrfree, int numext, const Variable alpha, const Variable beta)
CFFList ZFactorizeMultivariate(const CanonicalForm &f, bool issqrfree)
CFFList ZFactorizeUnivariate(const CanonicalForm &ff, bool issqrfree=false)