facFqFactorize.h File Reference

This file provides functions for factorizing a multivariate polynomial over 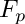, or GF. More...

#include "timing.h"
#include "facFqBivar.h"
#include "DegreePattern.h"
#include "ExtensionInfo.h"
#include "cf_util.h"
#include "facFqSquarefree.h"
#include "facFqBivarUtil.h"

Go to the source code of this file.

Functions
	TIMING_DEFINE_PRINT (fac_fq_squarefree) TIMING_DEFINE_PRINT(fac_fq_factor_squarefree) CFList multiFactorize(const CanonicalForm &F
	Factorization over a finite field. More...
CFList	FpSqrfFactorize (const CanonicalForm &F)
	factorize a squarefree multivariate polynomial over More...
CFList	FqSqrfFactorize (const CanonicalForm &F, const Variable &alpha)
	factorize a squarefree multivariate polynomial over More...
CFList	GFSqrfFactorize (const CanonicalForm &F)
	factorize a squarefree multivariate polynomial over GF More...
CFFList	FpFactorize (const CanonicalForm &G, bool substCheck=true)
	factorize a multivariate polynomial over More...
CFFList	FqFactorize (const CanonicalForm &G, const Variable &alpha, bool substCheck=true)
	factorize a multivariate polynomial over More...
CFFList	GFFactorize (const CanonicalForm &G, bool substCheck=true)
	factorize a multivariate polynomial over GF More...
CFList	extFactorRecombination (const CFList &factors, const CanonicalForm &F, const CFList &M, const ExtensionInfo &info, const CFList &evaluation)
	Naive factor recombination for multivariate factorization over an extension of the initial field. No precomputed is used to exclude combinations. More...
CFList	factorRecombination (const CanonicalForm &F, const CFList &factors, const CFList &M)
	Naive factor recombination for multivariate factorization. No precomputed is used to exclude combinations. More...
CFList	recombination (const CFList &factors1, const CFList &factors2, int s, int thres, const CanonicalForm &evalPoint, const Variable &x)
	recombination of bivariate factors factors1 s. t. the result evaluated at evalPoint coincides with factors2 More...
int	liftBoundAdaption (const CanonicalForm &F, const CFList &factors, bool &success, const int deg, const CFList &MOD, const int bound)
	Lift bound adaption. Essentially an early factor detection but only the lift bound is adapted. More...
int	extLiftBoundAdaption (const CanonicalForm &F, const CFList &factors, bool &success, const ExtensionInfo &info, const CFList &eval, const int deg, const CFList &MOD, const int bound)
	Lift bound adaption over an extension of the initial field. Essentially an early factor detection but only the lift bound is adapted. More...
CFList	earlyFactorDetect (CanonicalForm &F, CFList &factors, int &adaptedLiftBound, bool &success, const int deg, const CFList &MOD, const int bound)
	detects factors of F at stage deg of Hensel lifting. No combinations of more than one factor are tested. Lift bound is adapted. More...
CFList	extEarlyFactorDetect (CanonicalForm &F, CFList &factors, int &adaptedLiftBound, bool &success, const ExtensionInfo &info, const CFList &eval, const int deg, const CFList &MOD, const int bound)
	detects factors of F at stage deg of Hensel lifting. No combinations of more than one factor are tested. Lift bound is adapted. More...
CFList	evalPoints (const CanonicalForm &F, CFList &eval, const Variable &alpha, CFList &list, const bool &GF, bool &fail)
	evaluation point search for multivariate factorization, looks for a (F.level() - 1)-tuple such that the resulting univariate polynomial has main variable Variable (1), is squarefree and its degree coincides with degree(F) and the bivariate one is primitive wrt. Variable(1), and successively evaluated polynomials have the same degree in their main variable as F has, fails if there are no valid evaluation points, eval contains the intermediate evaluated polynomials. More...
CFList	henselLiftAndEarly (CanonicalForm &A, CFList &MOD, int *&liftBounds, bool &earlySuccess, CFList &earlyFactors, const CFList &Aeval, const CFList &biFactors, const CFList &evaluation, const ExtensionInfo &info)
	hensel Lifting and early factor detection More...
CFList	extFactorize (const CanonicalForm &F, const ExtensionInfo &info)
	Factorization over an extension of initial field. More...
CanonicalForm	lcmContent (const CanonicalForm &A, CFList &contentAi)
	compute the LCM of the contents of A wrt to each variable occuring in A. More...
CanonicalForm	myCompress (const CanonicalForm &F, CFMap &N)
	compress a polynomial s.t. and no gaps between the variables occur More...
void	evaluationWRTDifferentSecondVars (CFList *&Aeval, const CFList &evaluation, const CanonicalForm &A)
	evaluate a poly A with main variable at level 1 at an evaluation point in K^(n-1) wrt different second variables. If this evaluation is valid (see evalPoints) then Aeval contains A successively evaluated at this point, otherwise this entry is empty More...
void	refineBiFactors (const CanonicalForm &A, CFList &biFactors, CFList *const &factors, const CFList &evaluation, int minFactorsLength)
	refine a bivariate factorization of A with l factors to one with minFactorsLength if possible More...
CFList	buildUniFactors (const CFList &biFactors, const CanonicalForm &evalPoint, const Variable &y)
	plug in evalPoint for y in a list of polys More...
void	sortByUniFactors (CFList *&Aeval, int AevalLength, CFList &uniFactors, CFList &biFactors, const CFList &evaluation)
	sort bivariate factors in Aeval such that their corresponding univariate factors coincide with uniFactors, uniFactors and biFactors may get recombined if necessary More...
void	getLeadingCoeffs (const CanonicalForm &A, CFList *&Aeval)
	extract leading coefficients wrt Variable(1) from bivariate factors obtained from factorizations of A wrt different second variables More...
void	prepareLeadingCoeffs (CFList *&LCs, CanonicalForm &A, CFList &Aeval, int n, const CFList &leadingCoeffs, const CFList &biFactors, const CFList &evaluation)
	normalize precomputed leading coefficients such that leading coefficients evaluated at evaluation in K^(n-2) equal the leading coeffs wrt Variable(1) of bivariate factors and change A and Aeval accordingly More...
CFList	leadingCoeffReconstruction (const CanonicalForm &F, const CFList &factors, const CFList &M)
	obtain factors of F by reconstructing their leading coeffs More...
CFList	distributeContent (const CFList &L, const CFList *differentSecondVarFactors, int length)
	distribute content More...
void	gcdFreeBasis (CFFList &factors1, CFFList &factors2)
	gcd free basis of two lists of factors More...
CFList	precomputeLeadingCoeff (const CanonicalForm &LCF, const CFList &LCFFactors, const Variable &alpha, const CFList &evaluation, CFList *&differentSecondVarLCs, int lSecondVarLCs, Variable &y)
	computes a list l of length length(LCFFactors)+1 of polynomials such that prod (l)=LCF, note that the first entry of l may be non constant. Intended to be used to precompute coefficients of a polynomial f from its bivariate factorizations. More...
void	changeSecondVariable (CanonicalForm &A, CFList &biFactors, CFList &evaluation, CFList *&oldAeval, int lengthAeval2, const CFList &uniFactors, const Variable &w)
	changes the second variable to be w and updates all relevant data More...
void	distributeLCmultiplier (CanonicalForm &A, CFList &leadingCoeffs, CFList &biFactors, const CFList &evaluation, const CanonicalForm &LCmultipler)
	distributes a divisor LCmultiplier of LC(A,1) on the bivariate factors and the precomputed leading coefficients More...
void	LCHeuristic (CanonicalForm &A, const CanonicalForm &LCmultiplier, CFList &biFactors, CFList *&leadingCoeffs, const CFList *oldAeval, int lengthAeval, const CFList &evaluation, const CFList &oldBiFactors)
	heuristic to distribute LCmultiplier onto factors based on the variables that occur in LCmultiplier and in the leading coeffs of bivariate factors More...
void	LCHeuristicCheck (const CFList &LCs, const CFList &contents, CanonicalForm &A, const CanonicalForm &oldA, CFList &leadingCoeffs, bool &foundTrueMultiplier)
	checks if prod(LCs)==LC (oldA,1) and if so divides elements of leadingCoeffs by elements in contents, sets A to oldA and sets foundTrueMultiplier to true More...
void	LCHeuristic2 (const CanonicalForm &LCmultiplier, const CFList &factors, CFList &leadingCoeffs, CFList &contents, CFList &LCs, bool &foundTrueMultiplier)
	heuristic to distribute LCmultiplier onto factors based on the contents of factors. factors are assumed to come from LucksWangSparseHeuristic. If not successful contents will contain the content of each element of factors and LCs will contain the LC of each element of factors divided by its content More...
void	LCHeuristic3 (const CanonicalForm &LCmultiplier, const CFList &factors, const CFList &oldBiFactors, const CFList &contents, const CFList *oldAeval, CanonicalForm &A, CFList *&leadingCoeffs, int lengthAeval, bool &foundMultiplier)
	heuristic to remove LCmultiplier from a factor based on the contents of factors. factors are assumed to come from LucksWangSparseHeuristic. More...
void	LCHeuristic4 (const CFList &oldBiFactors, const CFList *oldAeval, const CFList &contents, const CFList &factors, const CanonicalForm &testVars, int lengthAeval, CFList *&leadingCoeffs, CanonicalForm &A, CanonicalForm &LCmultiplier, bool &foundMultiplier)
	heuristic to remove factors of LCmultiplier from factors. More precisely checks if elements of contents divide LCmultiplier. Assumes LCHeuristic3 is run before it and was successful. More...

Variables
const ExtensionInfo &	info
	< [in] sqrfree poly More...

Detailed Description

This file provides functions for factorizing a multivariate polynomial over 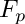, or GF.

Author

Martin Lee

Definition in file facFqFactorize.h.

Function Documentation

buildUniFactors()

CFList buildUniFactors	(	const CFList &	biFactors,
		const CanonicalForm &	evalPoint,
		const Variable &	y
	)

plug in evalPoint for y in a list of polys

Returns

returns a list of the evaluated polys, these evaluated polys are made monic

Parameters

[in]	biFactors	a list of polys
[in]	evalPoint	some evaluation point
[in]	y	some variable

Definition at line 2320 of file facFqFactorize.cc.

{
  CFList result;
  CanonicalForm tmp;
  for (CFListIterator i= biFactors; i.hasItem(); i++)
  {
    tmp= mod (i.getItem(), y - evalPoint);
    tmp /= Lc (tmp);
    result.append (tmp);
  }
  return result;
}

changeSecondVariable()

void changeSecondVariable	(	CanonicalForm &	A,
		CFList &	biFactors,
		CFList &	evaluation,
		CFList *&	oldAeval,
		int	lengthAeval2,
		const CFList &	uniFactors,
		const Variable &	w
	)

changes the second variable to be w and updates all relevant data

Parameters

[in,out]	A	a multivariate poly
[in,out]	biFactors	bivariate factors
[in,out]	evaluation	evaluation point
[in,out]	oldAeval	old bivariate factors wrt. different second vars
[in]	lengthAeval2	length of oldAeval
[in]	uniFactors	univariate factors
[in]	w	some variable

Definition at line 2543 of file facFqFactorize.cc.

{
  Variable y= Variable (2);
  A= swapvar (A, y, w);
  int i= A.level();
  CanonicalForm evalPoint;
  for (CFListIterator iter= evaluation; iter.hasItem(); iter++, i--)
  {
    if (i == w.level())
    {
      evalPoint= iter.getItem();
      iter.getItem()= evaluation.getLast();
      evaluation.removeLast();
      evaluation.append (evalPoint);
      break;
    }
  }
  for (i= 0; i < lengthAeval2; i++)
  {
    if (oldAeval[i].isEmpty())
      continue;
    if (oldAeval[i].getFirst().level() == w.level())
    {
      CFArray tmp= copy (oldAeval[i]);
      oldAeval[i]= biFactors;
      for (CFListIterator iter= oldAeval[i]; iter.hasItem(); iter++)
        iter.getItem()= swapvar (iter.getItem(), w, y);
      for (int ii= 0; ii < tmp.size(); ii++)
        tmp[ii]= swapvar (tmp[ii], w, y);
      CFArray tmp2= CFArray (tmp.size());
      CanonicalForm buf;
      for (int ii= 0; ii < tmp.size(); ii++)
      {
        buf= tmp[ii] (evaluation.getLast(),y);
        buf /= Lc (buf);
        tmp2[findItem (uniFactors, buf)-1]=tmp[ii];
      }
      biFactors= CFList();
      for (int j= 0; j < tmp2.size(); j++)
        biFactors.append (tmp2[j]);
    }
  }
}

distributeContent()

CFList distributeContent	(	const CFList &	L,
		const CFList *	differentSecondVarFactors,
		int	length
	)

distribute content

Returns

returns a list result of polys such that prod (result)= prod (L) but the first entry of L may be (partially) factorized and these factors are distributed onto other entries in L

Parameters

[in]	L	list of polys, first entry the content to be distributed
[in]	differentSecondVarFactors	factorization wrt different second vars
[in]	length	length ofdifferentSecondVarFactors

Definition at line 1294 of file facFqFactorize.cc.

{
  CFList l= L;
  CanonicalForm content= l.getFirst();
 
  if (content.inCoeffDomain())
    return l;
 
  if (l.length() == 1)
  {
    CFList result;
    for (int i= 0; i < length; i++)
    {
      if (differentSecondVarFactors[i].isEmpty())
        continue;
      if (result.isEmpty())
      {
        result= differentSecondVarFactors[i];
        for (CFListIterator iter= result; iter.hasItem(); iter++)
          content /= iter.getItem();
      }
      else
      {
        CFListIterator iter1= result;
        for (CFListIterator iter2= differentSecondVarFactors[i];iter2.hasItem();
             iter2++, iter1++)
        {
          iter1.getItem() *= iter2.getItem();
          content /= iter2.getItem();
        }
      }
    }
    result.insert (content);
    return result;
  }
 
  Variable v;
  CFListIterator iter1, iter2;
  CanonicalForm tmp, g;
  CFList multiplier;
  for (int i= 0; i < length; i++)
  {
    if (differentSecondVarFactors[i].isEmpty())
      continue;
    iter1= l;
    iter1++;
 
    tmp= 1;
    for (iter2= differentSecondVarFactors[i]; iter2.hasItem();
         iter2++, iter1++)
    {
      if (iter2.getItem().inCoeffDomain())
      {
        multiplier.append (1);
        continue;
      }
      v= iter2.getItem().mvar();
      if (degree (iter2.getItem()) == degree (iter1.getItem(),v))
      {
        multiplier.append (1);
        continue;
      }
      g= gcd (iter2.getItem(), content);
      if (!g.inCoeffDomain())
      {
        tmp *= g;
        multiplier.append (g);
      }
      else
        multiplier.append (1);
    }
    if (!tmp.isOne() && fdivides (tmp, content))
    {
      iter1= l;
      iter1++;
      content /= tmp;
      for (iter2= multiplier; iter2.hasItem(); iter1++, iter2++)
        iter1.getItem() *= iter2.getItem();
    }
    multiplier= CFList();
  }
 
  l.removeFirst();
  l.insert (content);
  return l;
}

distributeLCmultiplier()

void distributeLCmultiplier	(	CanonicalForm &	A,
		CFList &	leadingCoeffs,
		CFList &	biFactors,
		const CFList &	evaluation,
		const CanonicalForm &	LCmultipler
	)

distributes a divisor LCmultiplier of LC(A,1) on the bivariate factors and the precomputed leading coefficients

Parameters

[in,out]	A	some poly
[in,out]	leadingCoeffs	leading coefficients
[in,out]	biFactors	bivariate factors
[in]	evaluation	eval. point
[in]	LCmultipler	multiplier

Definition at line 2590 of file facFqFactorize.cc.

{
  CanonicalForm tmp= power (LCmultipler, biFactors.length() - 1);
  A *= tmp;
  tmp= LCmultipler;
  CFListIterator iter= leadingCoeffs;
  for (;iter.hasItem(); iter++)
    iter.getItem() *= LCmultipler;
  iter= evaluation;
  for (int i= A.level(); i > 2; i--, iter++)
    tmp= tmp (iter.getItem(), i);
  if (!tmp.inCoeffDomain())
  {
    for (CFListIterator i= biFactors; i.hasItem(); i++)
    {
      i.getItem() *= tmp/LC (i.getItem(), 1);
      i.getItem() /= Lc (i.getItem());
    }
  }
}

earlyFactorDetect()

CFList earlyFactorDetect	(	CanonicalForm &	F,
		CFList &	factors,
		int &	adaptedLiftBound,
		bool &	success,
		const int	deg,
		const CFList &	MOD,
		const int	bound
	)

detects factors of F at stage deg of Hensel lifting. No combinations of more than one factor are tested. Lift bound is adapted.

Returns

earlyFactorDetect returns a list of factors of F (possibly incomplete), in case of success. Otherwise an empty list.

See also

factorRecombination(), extEarlyFactorDetect()

Parameters

[in,out]	F	poly to be factored, returns poly divided by detected factors in case of success
[in,out]	factors	list of factors lifted up to deg, returns a list of factors without detected factors
[in,out]	adaptedLiftBound	adapted lift bound
[in,out]	success	indicating success
[in]	deg	stage of Hensel lifting
[in]	MOD	a list of powers of Variables
[in]	bound	initial lift bound

Definition at line 611 of file facFqFactorize.cc.

{
  CFList result;
  CFList T= factors;
  CanonicalForm buf= F;
  Variable y= F.mvar();
  Variable x= Variable (1);
  CanonicalForm LCBuf= LC (buf, x);
  CanonicalForm g, quot;
  CFList M= MOD;
  M.append (power (y, deg));
  adaptedLiftBound= 0;
  int d= bound;
  int e= 0;
  int nBuf;
  for (CFListIterator i= factors; i.hasItem(); i++)
  {
    g= mulMod (i.getItem(), LCBuf, M);
    g /= myContent (g);
    if (fdivides (g, buf, quot))
    {
      result.append (g);
      nBuf= degree (g, y) + degree (LC (g, x), y);
      d -= nBuf;
      e= tmax (e, nBuf);
      buf= quot;
      LCBuf= LC (buf, x);
      T= Difference (T, CFList (i.getItem()));
    }
  }
  adaptedLiftBound= d;
 
  if (adaptedLiftBound < deg)
  {
    if (adaptedLiftBound < degree (F) + 1)
    {
      if (d == 1)
        adaptedLiftBound= tmin (e + 1, deg);
      else
        adaptedLiftBound= deg;
    }
    factors= T;
    F= buf;
    success= true;
  }
  return result;
}

evalPoints()

CFList evalPoints	(	const CanonicalForm &	F,
		CFList &	eval,
		const Variable &	alpha,
		CFList &	list,
		const bool &	GF,
		bool &	fail
	)

evaluation point search for multivariate factorization, looks for a (F.level() - 1)-tuple such that the resulting univariate polynomial has main variable Variable (1), is squarefree and its degree coincides with degree(F) and the bivariate one is primitive wrt. Variable(1), and successively evaluated polynomials have the same degree in their main variable as F has, fails if there are no valid evaluation points, eval contains the intermediate evaluated polynomials.

Returns

evalPoints returns an evaluation point, which is valid if and only if fail == false.

Parameters

[in]	F	a compressed poly
[in,out]	eval	an empty list, returns F successive evaluated
[in]	alpha	algebraic variable
[in,out]	list	a list of points already considered, a point is encoded as a poly of degree F.level()-1 in Variable(1)
[in]	GF	GF?
[in,out]	fail	indicates failure

Definition at line 750 of file facFqFactorize.cc.

{
  int k= F.level() - 1;
  Variable x= Variable (1);
  CanonicalForm LCF=LC (F, x);
  CFList LCFeval;
 
  CFList result;
  FFRandom genFF;
  GFRandom genGF;
  int p= getCharacteristic ();
  if (p < CHAR_THRESHOLD)
  {
    if (!GF && alpha.level() == 1)
    {
      fail= true;
      return CFList();
    }
    else if (!GF && alpha.level() != 1)
    {
      if ((p == 2 && degree (getMipo (alpha)) < 6) ||
          (p == 3 && degree (getMipo (alpha)) < 4) ||
          (p == 5 && degree (getMipo (alpha)) < 3))
      {
        fail= true;
        return CFList();
      }
    }
  }
  double bound;
  if (alpha != x)
  {
    bound= pow ((double) p, (double) degree (getMipo(alpha)));
    bound *= (double) k;
  }
  else if (GF)
  {
    bound= pow ((double) p, (double) getGFDegree());
    bound *= (double) k;
  }
  else
    bound= pow ((double) p, (double) k);
 
  CanonicalForm random;
  CanonicalForm deriv_x, gcd_deriv;
  do
  {
    random= 0;
    // possible overflow if list.length() does not fit into a int
    if (list.length() >= bound)
    {
      fail= true;
      break;
    }
    for (int i= 0; i < k; i++)
    {
      if (list.isEmpty())
        result.append (0);
      else if (GF)
      {
        result.append (genGF.generate());
        random += result.getLast()*power (x, i);
      }
      else if (alpha.level() != 1)
      {
        AlgExtRandomF genAlgExt (alpha);
        result.append (genAlgExt.generate());
        random += result.getLast()*power (x, i);
      }
      else
      {
        result.append (genFF.generate());
        random += result.getLast()*power (x, i);
      }
    }
    if (find (list, random))
    {
      result= CFList();
      continue;
    }
    int l= F.level();
    eval.insert (F);
    LCFeval.insert (LCF);
    bool bad= false;
    for (CFListIterator i= result; i.hasItem(); i++, l--)
    {
      eval.insert (eval.getFirst()(i.getItem(), l));
      LCFeval.insert (LCFeval.getFirst()(i.getItem(), l));
      if (degree (eval.getFirst(), l - 1) != degree (F, l - 1))
      {
        if (!find (list, random))
          list.append (random);
        result= CFList();
        eval= CFList();
        LCFeval= CFList();
        bad= true;
        break;
      }
      if ((l != 2) && (degree (LCFeval.getFirst(), l-1) != degree (LCF, l-1)))
      {
        if (!find (list, random))
          list.append (random);
        result= CFList();
        eval= CFList();
        LCFeval= CFList();
        bad= true;
        break;
      }
    }
 
    if (bad)
      continue;
 
    if (degree (eval.getFirst()) != degree (F, 1))
    {
      if (!find (list, random))
        list.append (random);
      result= CFList();
      LCFeval= CFList();
      eval= CFList();
      continue;
    }
 
    deriv_x= deriv (eval.getFirst(), x);
    gcd_deriv= gcd (eval.getFirst(), deriv_x);
    if (degree (gcd_deriv) > 0)
    {
      if (!find (list, random))
        list.append (random);
      result= CFList();
      LCFeval= CFList();
      eval= CFList();
      continue;
    }
    CFListIterator i= eval;
    i++;
    CanonicalForm contentx= content (i.getItem(), x);
    if (degree (contentx) > 0)
    {
      if (!find (list, random))
        list.append (random);
      result= CFList();
      LCFeval= CFList();
      eval= CFList();
      continue;
    }
 
    contentx= content (i.getItem());
    if (degree (contentx) > 0)
    {
      if (!find (list, random))
        list.append (random);
      result= CFList();
      LCFeval= CFList();
      eval= CFList();
      continue;
    }
 
    if (list.length() >= bound)
    {
      fail= true;
      break;
    }
  } while (find (list, random));
 
  if (!eval.isEmpty())
    eval.removeFirst();
 
  return result;
}

evaluationWRTDifferentSecondVars()

void evaluationWRTDifferentSecondVars	(	CFList *&	Aeval,
		const CFList &	evaluation,
		const CanonicalForm &	A
	)

evaluate a poly A with main variable at level 1 at an evaluation point in K^(n-1) wrt different second variables. If this evaluation is valid (see evalPoints) then Aeval contains A successively evaluated at this point, otherwise this entry is empty

Parameters

[in,out]	Aeval	an array of length n-2 if variable at level i > 2 admits a valid evaluation this entry contains A successively evaluated at this point otherwise an empty list
[in]	evaluation	a valid evaluation point for main variable at level 1 and second variable at level 2
[in]	A	some poly

Definition at line 1965 of file facFqFactorize.cc.

{
  CanonicalForm tmp;
  CFList tmp2;
  CFListIterator iter;
  bool preserveDegree= true;
  Variable x= Variable (1);
  int j, degAi, degA1= degree (A,1);
  for (int i= A.level(); i > 2; i--)
  {
    tmp= A;
    tmp2= CFList();
    iter= evaluation;
    preserveDegree= true;
    degAi= degree (A,i);
    for (j= A.level(); j > 1; j--, iter++)
    {
      if (j == i)
        continue;
      else
      {
        tmp= tmp (iter.getItem(), j);
        tmp2.insert (tmp);
        if ((degree (tmp, i) != degAi) ||
            (degree (tmp, 1) != degA1))
        {
          preserveDegree= false;
          break;
        }
      }
    }
    if (!content(tmp,1).inCoeffDomain())
      preserveDegree= false;
    if (!content(tmp).inCoeffDomain())
      preserveDegree= false;
    if (!(gcd (deriv (tmp,x), tmp)).inCoeffDomain())
      preserveDegree= false;
    if (preserveDegree)
      Aeval [i - 3]= tmp2;
    else
      Aeval [i - 3]= CFList();
  }
}

extEarlyFactorDetect()

CFList extEarlyFactorDetect	(	CanonicalForm &	F,
		CFList &	factors,
		int &	adaptedLiftBound,
		bool &	success,
		const ExtensionInfo &	info,
		const CFList &	eval,
		const int	deg,
		const CFList &	MOD,
		const int	bound
	)

detects factors of F at stage deg of Hensel lifting. No combinations of more than one factor are tested. Lift bound is adapted.

Returns

extEarlyFactorDetect returns a list of factors of F (possibly incomplete), whose shift to zero is reversed, in case of success. Otherwise an empty list.

See also

factorRecombination(), earlyFactorDetection()

Parameters

[in,out]	F	poly to be factored, returns poly divided by detected factors in case of success
[in,out]	factors	list of factors lifted up to deg, returns a list of factors without detected factors
[in,out]	adaptedLiftBound	adapted lift bound
[in,out]	success	indicating succes
[in]	info	info about extension
[in]	eval	evaluation point
[in]	deg	stage of Hensel lifting
[in]	MOD	a list of powers of Variables
[in]	bound	initial lift bound

Definition at line 664 of file facFqFactorize.cc.

{
  Variable alpha= info.getAlpha();
  Variable beta= info.getBeta();
  CanonicalForm gamma= info.getGamma();
  CanonicalForm delta= info.getDelta();
  int k= info.getGFDegree();
  CFList result;
  CFList T= factors;
  CanonicalForm buf= F;
  Variable y= F.mvar();
  Variable x= Variable (1);
  CanonicalForm LCBuf= LC (buf, x);
  CanonicalForm g, gg, quot;
  CFList M= MOD;
  M.append (power (y, deg));
  adaptedLiftBound= 0;
  int d= bound;
  int e= 0;
  int nBuf;
  CFList source, dest;
 
  int degMipoBeta= 1;
  if (!k && beta.level() != 1)
    degMipoBeta= degree (getMipo (beta));
 
  for (CFListIterator i= factors; i.hasItem(); i++)
  {
    g= mulMod (i.getItem(), LCBuf, M);
    g /= myContent (g);
    if (fdivides (g, buf, quot))
    {
      gg= reverseShift (g, eval);
      gg /= Lc (gg);
      if (!k && beta == x)
      {
        if (degree (gg, alpha) < degMipoBeta)
        {
          appendTestMapDown (result, gg, info, source, dest);
          buf= quot;
          nBuf= degree (g, y) + degree (LC (g, x), y);
          d -= nBuf;
          e= tmax (e, nBuf);
          LCBuf= LC (buf, x);
          T= Difference (T, CFList (i.getItem()));
        }
      }
      else
      {
        if (!isInExtension (gg, gamma, k, delta, source, dest))
        {
          appendTestMapDown (result, gg, info, source, dest);
          buf= quot;
          nBuf= degree (g, y) + degree (LC (g, x), y);
          d -= nBuf;
          e= tmax (e, nBuf);
          LCBuf= LC (buf, x);
          T= Difference (T, CFList (i.getItem()));
         }
      }
    }
  }
  adaptedLiftBound= d;
 
  if (adaptedLiftBound < deg)
  {
    if (adaptedLiftBound < degree (F) + 1)
    {
      if (d == 1)
        adaptedLiftBound= tmin (e + 1, deg);
      else
        adaptedLiftBound= deg;
    }
    success= true;
    factors= T;
    F= buf;
  }
  return result;
}

extFactorize()

CFList extFactorize	(	const CanonicalForm &	F,
		const ExtensionInfo &	info
	)

Factorization over an extension of initial field.

Returns

extFactorize returns factorization of F over initial field

See also

extBiFactorize(), multiFactorize()

Factorization over an extension of initial field.

Parameters

[in]	F	poly to be factored
[in]	info	info about extension

Definition at line 3660 of file facFqFactorize.cc.

{
  CanonicalForm A= F;
 
  Variable alpha= info.getAlpha();
  Variable beta= info.getBeta();
  int k= info.getGFDegree();
  char cGFName= info.getGFName();
  CanonicalForm delta= info.getDelta();
  bool GF= (CFFactory::gettype() == GaloisFieldDomain);
  Variable w= Variable (1);
 
  CFList factors;
  if (!GF && alpha == w)  // we are in F_p
  {
    CFList factors;
    bool extension= true;
    int p= getCharacteristic();
    if (p < 7)
    {
      if (p == 2)
        setCharacteristic (getCharacteristic(), 6, 'Z');
      else if (p == 3)
        setCharacteristic (getCharacteristic(), 4, 'Z');
      else if (p == 5)
        setCharacteristic (getCharacteristic(), 3, 'Z');
      ExtensionInfo info= ExtensionInfo (extension);
      A= A.mapinto();
      factors= multiFactorize (A, info);
 
      CanonicalForm mipo= gf_mipo;
      setCharacteristic (getCharacteristic());
      Variable vBuf= rootOf (mipo.mapinto());
      for (CFListIterator j= factors; j.hasItem(); j++)
        j.getItem()= GF2FalphaRep (j.getItem(), vBuf);
      prune (vBuf);
    }
    else if (p >= 7 && p*p < (1<<16)) // pass to GF if possible
    {
      setCharacteristic (getCharacteristic(), 2, 'Z');
      ExtensionInfo info= ExtensionInfo (extension);
      A= A.mapinto();
      factors= multiFactorize (A, info);
 
      CanonicalForm mipo= gf_mipo;
      setCharacteristic (getCharacteristic());
      Variable vBuf= rootOf (mipo.mapinto());
      for (CFListIterator j= factors; j.hasItem(); j++)
        j.getItem()= GF2FalphaRep (j.getItem(), vBuf);
      prune (vBuf);
    }
    else  // not able to pass to GF, pass to F_p(\alpha)
    {
      CanonicalForm mipo= randomIrredpoly (2, w);
      Variable v= rootOf (mipo);
      ExtensionInfo info= ExtensionInfo (v);
      factors= multiFactorize (A, info);
      prune (v);
    }
    return factors;
  }
  else if (!GF && (alpha != w)) // we are in F_p(\alpha)
  {
    if (k == 1) // need factorization over F_p
    {
      int extDeg= degree (getMipo (alpha));
      extDeg++;
      CanonicalForm mipo= randomIrredpoly (extDeg, w);
      Variable v= rootOf (mipo);
      ExtensionInfo info= ExtensionInfo (v);
      factors= multiFactorize (A, info);
      prune (v);
    }
    else
    {
      if (beta == w)
      {
        Variable v= chooseExtension (alpha, beta, k);
        CanonicalForm primElem, imPrimElem;
        bool primFail= false;
        Variable vBuf;
        primElem= primitiveElement (alpha, vBuf, primFail);
        ASSERT (!primFail, "failure in integer factorizer");
        if (primFail)
          ; //ERROR
        else
          imPrimElem= mapPrimElem (primElem, alpha, v);
 
        CFList source, dest;
        CanonicalForm bufA= mapUp (A, alpha, v, primElem, imPrimElem,
                                   source, dest);
        ExtensionInfo info= ExtensionInfo (v, alpha, imPrimElem, primElem);
        factors= multiFactorize (bufA, info);
        prune (v);
      }
      else
      {
        Variable v= chooseExtension (alpha, beta, k);
        CanonicalForm primElem, imPrimElem;
        bool primFail= false;
        Variable vBuf;
        ASSERT (!primFail, "failure in integer factorizer");
        if (primFail)
          ; //ERROR
        else
          imPrimElem= mapPrimElem (delta, beta, v);
 
        CFList source, dest;
        CanonicalForm bufA= mapDown (A, info, source, dest);
        source= CFList();
        dest= CFList();
        bufA= mapUp (bufA, beta, v, delta, imPrimElem, source, dest);
        ExtensionInfo info= ExtensionInfo (v, beta, imPrimElem, delta);
        factors= multiFactorize (bufA, info);
        prune (v);
      }
    }
    return factors;
  }
  else // we are in GF (p^k)
  {
    int p= getCharacteristic();
    int extensionDeg= getGFDegree();
    bool extension= true;
    if (k == 1) // need factorization over F_p
    {
      extensionDeg++;
      if (pow ((double) p, (double) extensionDeg) < (1<<16))
      // pass to GF(p^k+1)
      {
        CanonicalForm mipo= gf_mipo;
        setCharacteristic (p);
        Variable vBuf= rootOf (mipo.mapinto());
        A= GF2FalphaRep (A, vBuf);
        setCharacteristic (p, extensionDeg, 'Z');
        ExtensionInfo info= ExtensionInfo (extension);
        factors= multiFactorize (A.mapinto(), info);
        prune (vBuf);
      }
      else // not able to pass to another GF, pass to F_p(\alpha)
      {
        CanonicalForm mipo= gf_mipo;
        setCharacteristic (p);
        Variable vBuf= rootOf (mipo.mapinto());
        A= GF2FalphaRep (A, vBuf);
        Variable v= chooseExtension (vBuf, beta, k);
        ExtensionInfo info= ExtensionInfo (v, extension);
        factors= multiFactorize (A, info);
        prune (vBuf);
      }
    }
    else // need factorization over GF (p^k)
    {
      if (pow ((double) p, (double) 2*extensionDeg) < (1<<16))
      // pass to GF(p^2k)
      {
        setCharacteristic (p, 2*extensionDeg, 'Z');
        ExtensionInfo info= ExtensionInfo (k, cGFName, extension);
        factors= multiFactorize (GFMapUp (A, extensionDeg), info);
        setCharacteristic (p, extensionDeg, cGFName);
      }
      else // not able to pass to GF (p^2k), pass to F_p (\alpha)
      {
        CanonicalForm mipo= gf_mipo;
        setCharacteristic (p);
        Variable v1= rootOf (mipo.mapinto());
        A= GF2FalphaRep (A, v1);
        Variable v2= chooseExtension (v1, v1, k);
        CanonicalForm primElem, imPrimElem;
        bool primFail= false;
        Variable vBuf;
        primElem= primitiveElement (v1, v1, primFail);
        if (primFail)
          ; //ERROR
        else
          imPrimElem= mapPrimElem (primElem, v1, v2);
        CFList source, dest;
        CanonicalForm bufA= mapUp (A, v1, v2, primElem, imPrimElem,
                                     source, dest);
        ExtensionInfo info= ExtensionInfo (v2, v1, imPrimElem, primElem);
        factors= multiFactorize (bufA, info);
        setCharacteristic (p, k, cGFName);
        for (CFListIterator i= factors; i.hasItem(); i++)
          i.getItem()= Falpha2GFRep (i.getItem());
        prune (v1);
      }
    }
    return factors;
  }
}

extFactorRecombination()

CFList extFactorRecombination	(	const CFList &	factors,
		const CanonicalForm &	F,
		const CFList &	M,
		const ExtensionInfo &	info,
		const CFList &	evaluation
	)

Naive factor recombination for multivariate factorization over an extension of the initial field. No precomputed is used to exclude combinations.

Returns

extFactorRecombination returns a list of factors of F, whose shift to zero is reversed.

See also

factorRecombination()

Parameters

[in]	factors	list of lifted factors that are monic wrt Variable (1)
[in]	F	poly to be factored
[in]	M	a list of powers of Variables
[in]	info	info about extension
[in]	evaluation	evaluation point

Definition at line 215 of file facFqFactorize.cc.

{
  Variable alpha= info.getAlpha();
  Variable beta= info.getBeta();
  CanonicalForm gamma= info.getGamma();
  CanonicalForm delta= info.getDelta();
  int k= info.getGFDegree();
  CFList source, dest;
  if (factors.length() == 1)
  {
    CanonicalForm buf= reverseShift (F, evaluation);
    return CFList (mapDown (buf, info, source, dest));
  }
  if (factors.length() < 1)
    return CFList();
 
  int degMipoBeta= 1;
  if (!k && beta.level() != 1)
    degMipoBeta= degree (getMipo (beta));
 
  CFList T, S;
  T= factors;
 
  int s= 1;
  CFList result;
  CanonicalForm buf;
 
  buf= F;
 
  Variable x= Variable (1);
  CanonicalForm g, LCBuf= LC (buf, x);
  CanonicalForm buf2, quot;
  int * v= new int [T.length()];
  for (int i= 0; i < T.length(); i++)
    v[i]= 0;
  bool noSubset= false;
  CFArray TT;
  TT= copy (factors);
  bool recombination= false;
  bool trueFactor= false;
  while (T.length() >= 2*s)
  {
    while (noSubset == false)
    {
      if (T.length() == s)
      {
        delete [] v;
        if (recombination)
        {
          T.insert (LCBuf);
          g= prodMod (T, M);
          T.removeFirst();
          result.append (g/myContent (g));
          g= reverseShift (g, evaluation);
          g /= Lc (g);
          appendTestMapDown (result, g, info, source, dest);
          return result;
        }
        else
        {
          buf= reverseShift (buf, evaluation);
          return CFList (buf);
        }
      }
 
      S= subset (v, s, TT, noSubset);
      if (noSubset) break;
 
      S.insert (LCBuf);
      g= prodMod (S, M);
      S.removeFirst();
      g /= myContent (g);
      if (fdivides (g, buf, quot))
      {
        buf2= reverseShift (g, evaluation);
        buf2 /= Lc (buf2);
        if (!k && beta == x)
        {
          if (degree (buf2, alpha) < degMipoBeta)
          {
            appendTestMapDown (result, buf2, info, source, dest);
            buf= quot;
            LCBuf= LC (buf, x);
            recombination= true;
            trueFactor= true;
          }
        }
        else
        {
          if (!isInExtension (buf2, gamma, k, delta, source, dest))
          {
            appendTestMapDown (result, buf2, info, source, dest);
            buf /= g;
            LCBuf= LC (buf, x);
            recombination= true;
            trueFactor= true;
          }
        }
 
        if (trueFactor)
        {
          T= Difference (T, S);
 
          if (T.length() < 2*s || T.length() == s)
          {
            buf= reverseShift (buf, evaluation);
            buf /= Lc (buf);
            appendTestMapDown (result, buf, info, source, dest);
            delete [] v;
            return result;
          }
          trueFactor= false;
          TT= copy (T);
          indexUpdate (v, s, T.length(), noSubset);
          if (noSubset) break;
        }
      }
    }
    s++;
    if (T.length() < 2*s || T.length() == s)
    {
      buf= reverseShift (buf, evaluation);
      appendTestMapDown (result, buf, info, source, dest);
      delete [] v;
      return result;
    }
    for (int i= 0; i < T.length(); i++)
      v[i]= 0;
    noSubset= false;
  }
  if (T.length() < 2*s)
  {
    buf= reverseShift (F, evaluation);
    appendMapDown (result, buf, info, source, dest);
  }
 
  delete [] v;
  return result;
}

extLiftBoundAdaption()

int extLiftBoundAdaption	(	const CanonicalForm &	F,
		const CFList &	factors,
		bool &	success,
		const ExtensionInfo &	info,
		const CFList &	eval,
		const int	deg,
		const CFList &	MOD,
		const int	bound
	)

Lift bound adaption over an extension of the initial field. Essentially an early factor detection but only the lift bound is adapted.

Returns

liftBoundAdaption returns an adapted lift bound.

See also

earlyFactorDetect(), earlyFactorDetection()

Parameters

[in]	F	a poly
[in]	factors	list of list of lifted factors that are monic wrt
[in,out]	success	indicates that no further lifting is necessary
[in]	info	info about extension
[in]	eval	evaluation point
[in]	deg	stage of Hensel lifting
[in]	MOD	a list of powers of Variables
[in]	bound	initial lift bound

Definition at line 513 of file facFqFactorize.cc.

{
  Variable alpha= info.getAlpha();
  Variable beta= info.getBeta();
  CanonicalForm gamma= info.getGamma();
  CanonicalForm delta= info.getDelta();
  int k= info.getGFDegree();
  int adaptedLiftBound= 0;
  CanonicalForm buf= F;
  Variable y= F.mvar();
  Variable x= Variable (1);
  CanonicalForm LCBuf= LC (buf, x);
  CanonicalForm g, gg, quot;
  CFList M= MOD;
  M.append (power (y, deg));
  adaptedLiftBound= 0;
  int d= bound;
  int e= 0;
  int nBuf;
  int degMipoBeta= 1;
  if (!k && beta.level() != 1)
    degMipoBeta= degree (getMipo (beta));
 
  CFList source, dest;
  for (CFListIterator i= factors; i.hasItem(); i++)
  {
    g= mulMod (i.getItem(), LCBuf, M);
    g /= myContent (g);
    if (fdivides (g, buf, quot))
    {
      gg= reverseShift (g, eval);
      gg /= Lc (gg);
      if (!k && beta == x)
      {
        if (degree (gg, alpha) < degMipoBeta)
        {
          buf= quot;
          nBuf= degree (g, y) + degree (LC (g, x), y);
          d -= nBuf;
          e= tmax (e, nBuf);
          LCBuf= LC (buf, x);
        }
      }
      else
      {
        if (!isInExtension (gg, gamma, k, delta, source, dest))
        {
          buf= quot;
          nBuf= degree (g, y) + degree (LC (g, x), y);
          d -= nBuf;
          e= tmax (e, nBuf);
          LCBuf= LC (buf, x);
        }
      }
    }
  }
  adaptedLiftBound= d;
 
  if (adaptedLiftBound < deg)
  {
    if (adaptedLiftBound < degree (F) + 1)
    {
      if (d == 1)
      {
        if (e + 1 > deg)
        {
          adaptedLiftBound= deg;
          success= false;
        }
        else
        {
          success= true;
          if (e + 1 < degree (F) + 1)
            adaptedLiftBound= deg;
          else
            adaptedLiftBound= e + 1;
        }
      }
      else
      {
        success= true;
        adaptedLiftBound= deg;
      }
    }
    else
    {
      success= true;
    }
  }
 
  return adaptedLiftBound;
}

factorRecombination()

CFList factorRecombination	(	const CanonicalForm &	F,
		const CFList &	factors,
		const CFList &	M
	)

Naive factor recombination for multivariate factorization. No precomputed is used to exclude combinations.

Returns

factorRecombination returns a list of factors of F

See also

extFactorRecombination()

Parameters

[in]	F	poly to be factored
[in]	factors	list of lifted factors that are monic wrt Variable (1)
[in]	M	a list of powers of Variables

Definition at line 360 of file facFqFactorize.cc.

{
  if (factors.length() == 1)
    return CFList(F);
  if (factors.length() < 1)
    return CFList();
 
  CFList T, S;
 
  T= factors;
 
  int s= 1;
  CFList result;
  CanonicalForm LCBuf= LC (F, Variable (1));
  CanonicalForm g, buf= F;
  int * v= new int [T.length()];
  for (int i= 0; i < T.length(); i++)
    v[i]= 0;
  bool noSubset= false;
  CFArray TT;
  TT= copy (factors);
  Variable y= F.level() - 1;
  bool recombination= false;
  CanonicalForm h, quot;
  while (T.length() >= 2*s)
  {
    while (noSubset == false)
    {
      if (T.length() == s)
      {
        delete [] v;
        if (recombination)
        {
          T.insert (LC (buf));
          g= prodMod (T, M);
          result.append (g/myContent (g));
          return result;
        }
        else
          return CFList (F);
      }
      S= subset (v, s, TT, noSubset);
      if (noSubset) break;
      S.insert (LCBuf);
      g= prodMod (S, M);
      S.removeFirst();
      g /= myContent (g);
      if (fdivides (g, buf, quot))
      {
        recombination= true;
        result.append (g);
        buf= quot;
        LCBuf= LC (buf, Variable(1));
        T= Difference (T, S);
        if (T.length() < 2*s || T.length() == s)
        {
          result.append (buf);
          delete [] v;
          return result;
        }
        TT= copy (T);
        indexUpdate (v, s, T.length(), noSubset);
        if (noSubset) break;
      }
    }
    s++;
    if (T.length() < 2*s || T.length() == s)
    {
      result.append (buf);
      delete [] v;
      return result;
    }
    for (int i= 0; i < T.length(); i++)
      v[i]= 0;
    noSubset= false;
  }
  if (T.length() < 2*s)
    result.append (F);
 
  delete [] v;
  return result;
}

FpFactorize()

CFFList FpFactorize ( const CanonicalForm &  G, bool  substCheck = true  )

inline

factorize a multivariate polynomial over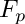

Returns

FpFactorize returns a list of monic factors with multiplicity, the first element is the leading coefficient.

See also

FqFactorize(), GFFactorize()

Parameters

[in]	G	a multivariate poly
[in]	substCheck	enables substitute check

Definition at line 101 of file facFqFactorize.h.

{
  if (getNumVars (G) == 2)
    return FpBiFactorize (G, substCheck);
 
  CanonicalForm F= G;
  if (substCheck)
  {
    bool foundOne= false;
    int * substDegree= NEW_ARRAY(int,F.level());
    for (int i= 1; i <= F.level(); i++)
    {
      if (degree (F, i) > 0)
      {
        substDegree[i-1]= substituteCheck (F, Variable (i));
        if (substDegree [i-1] > 1)
        {
          foundOne= true;
          subst (F, F, substDegree[i-1], Variable (i));
        }
      }
      else
        substDegree[i-1]= -1;
    }
    if (foundOne)
    {
      CFFList result= FpFactorize (F, false);
      CFFList newResult, tmp;
      CanonicalForm tmp2;
      newResult.insert (result.getFirst());
      result.removeFirst();
      for (CFFListIterator i= result; i.hasItem(); i++)
      {
        tmp2= i.getItem().factor();
        for (int j= 1; j <= G.level(); j++)
        {
          if (substDegree[j-1] > 1)
            tmp2= reverseSubst (tmp2, substDegree[j-1], Variable (j));
        }
        tmp= FpFactorize (tmp2, false);
        tmp.removeFirst();
        for (CFFListIterator j= tmp; j.hasItem(); j++)
          newResult.append (CFFactor (j.getItem().factor(),
                                      j.getItem().exp()*i.getItem().exp()));
      }
      DELETE_ARRAY(substDegree);
      return newResult;
    }
    DELETE_ARRAY(substDegree);
  }
 
  ExtensionInfo info= ExtensionInfo (false);
  Variable a= Variable (1);
  CanonicalForm LcF= Lc (F);
  TIMING_START (fac_fq_squarefree);
  CFFList sqrf= FpSqrf (F, false);
  TIMING_END_AND_PRINT (fac_fq_squarefree,
                        "time for squarefree factorization over Fq: ");
  CFFList result;
  CFList bufResult;
  sqrf.removeFirst();
  CFListIterator i;
  for (CFFListIterator iter= sqrf; iter.hasItem(); iter++)
  {
    TIMING_START (fac_fq_factor_squarefree);
    bufResult= multiFactorize (iter.getItem().factor(), info);
    TIMING_END_AND_PRINT (fac_fq_factor_squarefree,
                          "time to factorize sqrfree factor over Fq: ");
    for (i= bufResult; i.hasItem(); i++)
      result.append (CFFactor (i.getItem(), iter.getItem().exp()));
  }
  result.insert (CFFactor (LcF, 1));
  return result;
}

FpSqrfFactorize()

CFList FpSqrfFactorize ( const CanonicalForm &  F )

inline

factorize a squarefree multivariate polynomial over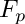

Returns

FpSqrfFactorize returns a list of monic factors, the first element is the leading coefficient.

See also

FqSqrfFactorize(), GFSqrfFactorize()

Parameters

[in]

F

a multivariate poly

Definition at line 47 of file facFqFactorize.h.

{
  if (getNumVars (F) == 2)
    return FpBiSqrfFactorize (F);
  ExtensionInfo info= ExtensionInfo (false);
  CFList result= multiFactorize (F, info);
  result.insert (Lc(F));
  return result;
}

FqFactorize()

CFFList FqFactorize ( const CanonicalForm &  G, const Variable &  alpha, bool  substCheck = true  )

inline

factorize a multivariate polynomial over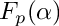

Returns

FqFactorize returns a list of monic factors with multiplicity, the first element is the leading coefficient.

See also

FpFactorize(), GFFactorize()

Parameters

[in]	G	a multivariate poly
[in]	alpha	algebraic variable
[in]	substCheck	enables substitute check

Definition at line 184 of file facFqFactorize.h.

{
  if (getNumVars (G) == 2)
    return FqBiFactorize (G, alpha, substCheck);
 
  CanonicalForm F= G;
  if (substCheck)
  {
    bool foundOne= false;
    int * substDegree= NEW_ARRAY(int,F.level());
    for (int i= 1; i <= F.level(); i++)
    {
      if (degree (F, i) > 0)
      {
        substDegree[i-1]= substituteCheck (F, Variable (i));
        if (substDegree [i-1] > 1)
        {
          foundOne= true;
          subst (F, F, substDegree[i-1], Variable (i));
        }
      }
      else
        substDegree[i-1]= -1;
    }
    if (foundOne)
    {
      CFFList result= FqFactorize (F, alpha, false);
      CFFList newResult, tmp;
      CanonicalForm tmp2;
      newResult.insert (result.getFirst());
      result.removeFirst();
      for (CFFListIterator i= result; i.hasItem(); i++)
      {
        tmp2= i.getItem().factor();
        for (int j= 1; j <= G.level(); j++)
        {
          if (substDegree[j-1] > 1)
            tmp2= reverseSubst (tmp2, substDegree[j-1], Variable (j));
        }
        tmp= FqFactorize (tmp2, alpha, false);
        tmp.removeFirst();
        for (CFFListIterator j= tmp; j.hasItem(); j++)
          newResult.append (CFFactor (j.getItem().factor(),
                                      j.getItem().exp()*i.getItem().exp()));
      }
      DELETE_ARRAY(substDegree);
      return newResult;
    }
    DELETE_ARRAY(substDegree);
  }
 
  ExtensionInfo info= ExtensionInfo (alpha, false);
  CanonicalForm LcF= Lc (F);
  TIMING_START (fac_fq_squarefree);
  CFFList sqrf= FqSqrf (F, alpha, false);
  TIMING_END_AND_PRINT (fac_fq_squarefree,
                        "time for squarefree factorization over Fq: ");
  CFFList result;
  CFList bufResult;
  sqrf.removeFirst();
  CFListIterator i;
  for (CFFListIterator iter= sqrf; iter.hasItem(); iter++)
  {
    TIMING_START (fac_fq_factor_squarefree);
    bufResult= multiFactorize (iter.getItem().factor(), info);
    TIMING_END_AND_PRINT (fac_fq_factor_squarefree,
                          "time to factorize sqrfree factor over Fq: ");
    for (i= bufResult; i.hasItem(); i++)
      result.append (CFFactor (i.getItem(), iter.getItem().exp()));
  }
  result.insert (CFFactor (LcF, 1));
  return result;
}

FqSqrfFactorize()

CFList FqSqrfFactorize ( const CanonicalForm &  F, const Variable &  alpha  )

inline

factorize a squarefree multivariate polynomial over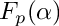

Returns

FqSqrfFactorize returns a list of monic factors, the first element is the leading coefficient.

See also

FpSqrfFactorize(), GFSqrfFactorize()

Parameters

[in]	F	a multivariate poly
[in]	alpha	algebraic variable

Definition at line 64 of file facFqFactorize.h.

{
  if (getNumVars (F) == 2)
    return FqBiSqrfFactorize (F, alpha);
  ExtensionInfo info= ExtensionInfo (alpha, false);
  CFList result= multiFactorize (F, info);
  result.insert (Lc(F));
  return result;
}

gcdFreeBasis()

void gcdFreeBasis	(	CFFList &	factors1,
		CFFList &	factors2
	)

gcd free basis of two lists of factors

Parameters

[in,out]	factors1	list of factors, returns gcd free factors
[in,out]	factors2	list of factors, returns gcd free factors

Definition at line 1268 of file facFqFactorize.cc.

{
  CanonicalForm g;
  int k= factors1.length();
  int l= factors2.length();
  int n= 0;
  int m;
  CFFListIterator j;
  for (CFFListIterator i= factors1; (n < k && i.hasItem()); i++, n++)
  {
    m= 0;
    for (j= factors2; (m < l && j.hasItem()); j++, m++)
    {
      g= gcd (i.getItem().factor(), j.getItem().factor());
      if (degree (g,1) > 0)
      {
        j.getItem()= CFFactor (j.getItem().factor()/g, j.getItem().exp());
        i.getItem()= CFFactor (i.getItem().factor()/g, i.getItem().exp());
        factors1.append (CFFactor (g, i.getItem().exp()));
        factors2.append (CFFactor (g, j.getItem().exp()));
      }
    }
  }
}

getLeadingCoeffs()

void getLeadingCoeffs	(	const CanonicalForm &	A,
		CFList *&	Aeval
	)

extract leading coefficients wrt Variable(1) from bivariate factors obtained from factorizations of A wrt different second variables

Parameters

[in]	A	some poly
[in,out]	Aeval	array of bivariate factors, returns the leading coefficients of these factors

Definition at line 2232 of file facFqFactorize.cc.

{
  CFListIterator iter;
  CFList LCs;
  for (int j= 0; j < A.level() - 2; j++)
  {
    if (!Aeval[j].isEmpty())
    {
      LCs= CFList();
      for (iter= Aeval[j]; iter.hasItem(); iter++)
        LCs.append (LC (iter.getItem(), 1));
      //normalize (LCs);
      Aeval[j]= LCs;
    }
  }
}

GFFactorize()

CFFList GFFactorize ( const CanonicalForm &  G, bool  substCheck = true  )

inline

factorize a multivariate polynomial over GF

Returns

GFFactorize returns a list of monic factors with multiplicity, the first element is the leading coefficient.

See also

FpFactorize(), FqFactorize()

Parameters

[in]	G	a multivariate poly
[in]	substCheck	enables substitute check

Definition at line 267 of file facFqFactorize.h.

{
  ASSERT (CFFactory::gettype() == GaloisFieldDomain,
          "GF as base field expected");
  if (getNumVars (G) == 2)
    return GFBiFactorize (G, substCheck);
 
  CanonicalForm F= G;
  if (substCheck)
  {
    bool foundOne= false;
    int * substDegree= NEW_ARRAY(int,F.level());
    for (int i= 1; i <= F.level(); i++)
    {
      if (degree (F, i) > 0)
      {
        substDegree[i-1]= substituteCheck (F, Variable (i));
        if (substDegree [i-1] > 1)
        {
          foundOne= true;
          subst (F, F, substDegree[i-1], Variable (i));
        }
      }
      else
        substDegree[i-1]= -1;
    }
    if (foundOne)
    {
      CFFList result= GFFactorize (F, false);
      CFFList newResult, tmp;
      CanonicalForm tmp2;
      newResult.insert (result.getFirst());
      result.removeFirst();
      for (CFFListIterator i= result; i.hasItem(); i++)
      {
        tmp2= i.getItem().factor();
        for (int j= 1; j <= G.level(); j++)
        {
          if (substDegree[j-1] > 1)
            tmp2= reverseSubst (tmp2, substDegree[j-1], Variable (j));
        }
        tmp= GFFactorize (tmp2, false);
        tmp.removeFirst();
        for (CFFListIterator j= tmp; j.hasItem(); j++)
          newResult.append (CFFactor (j.getItem().factor(),
                                      j.getItem().exp()*i.getItem().exp()));
      }
      DELETE_ARRAY(substDegree);
      return newResult;
    }
    DELETE_ARRAY(substDegree);
  }
 
  Variable a= Variable (1);
  ExtensionInfo info= ExtensionInfo (getGFDegree(), gf_name, false);
  CanonicalForm LcF= Lc (F);
  CFFList sqrf= GFSqrf (F, false);
  CFFList result;
  CFList bufResult;
  sqrf.removeFirst();
  CFListIterator i;
  for (CFFListIterator iter= sqrf; iter.hasItem(); iter++)
  {
    bufResult= multiFactorize (iter.getItem().factor(), info);
    for (i= bufResult; i.hasItem(); i++)
      result.append (CFFactor (i.getItem(), iter.getItem().exp()));
  }
  result.insert (CFFactor (LcF, 1));
  return result;
}

GFSqrfFactorize()

CFList GFSqrfFactorize ( const CanonicalForm &  F )

inline

factorize a squarefree multivariate polynomial over GF

Returns

GFSqrfFactorize returns a list of monic factors, the first element is the leading coefficient.

See also

FpSqrfFactorize(), FqSqrfFactorize()

Parameters

[in]

F

a multivariate poly

Definition at line 82 of file facFqFactorize.h.

{
  ASSERT (CFFactory::gettype() == GaloisFieldDomain,
          "GF as base field expected");
  if (getNumVars (F) == 2)
    return GFBiSqrfFactorize (F);
  ExtensionInfo info= ExtensionInfo (getGFDegree(), gf_name, false);
  CFList result= multiFactorize (F, info);
  result.insert (Lc(F));
  return result;
}

henselLiftAndEarly()

CFList henselLiftAndEarly	(	CanonicalForm &	A,
		CFList &	MOD,
		int *&	liftBounds,
		bool &	earlySuccess,
		CFList &	earlyFactors,
		const CFList &	Aeval,
		const CFList &	biFactors,
		const CFList &	evaluation,
		const ExtensionInfo &	info
	)

hensel Lifting and early factor detection

Returns

henselLiftAndEarly returns monic (wrt Variable (1)) lifted factors without factors which have been detected at an early stage of Hensel lifting

See also

earlyFactorDetectn(), extEarlyFactorDetect()

Parameters

[in,out]	A	poly to be factored, returns poly divided by detected factors, in case of success
[in,out]	MOD	a list of powers of Variables
[in,out]	liftBounds	initial lift bounds, returns adapted lift bounds
[in,out]	earlySuccess	indicating success
[in,out]	earlyFactors	early factors
[in]	Aeval	A successively evaluated at elements of evaluation@param biFactors bivariate factors
[in]	evaluation	evaluation point
[in]	info	info about extension

Definition at line 984 of file facFqFactorize.cc.

{
  bool extension= info.isInExtension();
  CFList bufFactors= biFactors;
  bufFactors.insert (LC (Aeval.getFirst(), 1));
 
  sortList (bufFactors, Variable (1));
 
  CFList diophant;
  CFArray Pi;
  int smallFactorDeg= 11; //tunable parameter
  CFList result;
  int adaptedLiftBound= 0;
  int liftBound= liftBounds[1];
 
  earlySuccess= false;
  CFList earlyReconstFactors;
  CFListIterator j= Aeval;
  j++;
  CanonicalForm buf= j.getItem();
  CFMatrix Mat= CFMatrix (liftBound, bufFactors.length() - 1);
  MOD= CFList (power (Variable (2), liftBounds[0]));
  if (smallFactorDeg >= liftBound)
  {
    result= henselLift23 (Aeval, bufFactors, liftBounds, diophant, Pi, Mat);
  }
  else if (smallFactorDeg >= degree (buf) + 1)
  {
    liftBounds[1]= degree (buf) + 1;
    result= henselLift23 (Aeval, bufFactors, liftBounds, diophant, Pi, Mat);
    if (Aeval.length() == 2)
    {
      if (!extension)
        earlyFactors= earlyFactorDetect
                       (buf, result, adaptedLiftBound, earlySuccess,
                        degree (buf) + 1, MOD, liftBound);
      else
        earlyFactors= extEarlyFactorDetect
                       (buf, result, adaptedLiftBound, earlySuccess,
                        info, evaluation, degree
                        (buf) + 1, MOD, liftBound);
    }
    else
    {
      if (!extension)
        adaptedLiftBound= liftBoundAdaption (buf, result, earlySuccess,
                                             degree (buf) + 1, MOD, liftBound);
      else
        adaptedLiftBound= extLiftBoundAdaption (buf, result, earlySuccess, info,
                                                evaluation, degree (buf) + 1,
                                                MOD, liftBound);
    }
    if (!earlySuccess)
    {
      result.insert (LC (buf, 1));
      liftBounds[1]= adaptedLiftBound;
      liftBound= adaptedLiftBound;
      henselLiftResume (buf, result, degree (buf) + 1, liftBound,
                        Pi, diophant, Mat, MOD);
    }
    else
      liftBounds[1]= adaptedLiftBound;
  }
  else if (smallFactorDeg < degree (buf) + 1)
  {
    liftBounds[1]= smallFactorDeg;
    result= henselLift23 (Aeval, bufFactors, liftBounds, diophant, Pi, Mat);
    if (Aeval.length() == 2)
    {
      if (!extension)
        earlyFactors= earlyFactorDetect (buf, result, adaptedLiftBound,
                                         earlySuccess, smallFactorDeg, MOD,
                                         liftBound);
      else
        earlyFactors= extEarlyFactorDetect (buf, result, adaptedLiftBound,
                                            earlySuccess, info, evaluation,
                                            smallFactorDeg, MOD, liftBound);
    }
    else
    {
      if (!extension)
        adaptedLiftBound= liftBoundAdaption (buf, result, earlySuccess,
                                             smallFactorDeg, MOD, liftBound);
      else
        adaptedLiftBound= extLiftBoundAdaption (buf, result, earlySuccess, info,
                                                evaluation, smallFactorDeg, MOD,
                                                liftBound);
    }
 
    if (!earlySuccess)
    {
      result.insert (LC (buf, 1));
      henselLiftResume (buf, result, smallFactorDeg, degree (buf) + 1,
                        Pi, diophant, Mat, MOD);
      if (Aeval.length() == 2)
      {
         if (!extension)
           earlyFactors= earlyFactorDetect (buf, result, adaptedLiftBound,
                                            earlySuccess, degree (buf) + 1,
                                            MOD, liftBound);
         else
           earlyFactors= extEarlyFactorDetect (buf, result, adaptedLiftBound,
                                               earlySuccess, info, evaluation,
                                               degree (buf) + 1, MOD,
                                               liftBound);
      }
      else
      {
        if (!extension)
          adaptedLiftBound= liftBoundAdaption (buf, result, earlySuccess,
                                               degree (buf) + 1, MOD,liftBound);
        else
          adaptedLiftBound= extLiftBoundAdaption (buf, result, earlySuccess,
                                                  info, evaluation,
                                                  degree (buf) + 1, MOD,
                                                  liftBound);
      }
      if (!earlySuccess)
      {
        result.insert (LC (buf, 1));
        liftBounds[1]= adaptedLiftBound;
        liftBound= adaptedLiftBound;
        henselLiftResume (buf, result, degree (buf) + 1, liftBound,
                          Pi, diophant, Mat, MOD);
      }
      else
        liftBounds[1]= adaptedLiftBound;
    }
    else
      liftBounds[1]= adaptedLiftBound;
  }
 
  MOD.append (power (Variable (3), liftBounds[1]));
 
  if (Aeval.length() > 2)
  {
    CFListIterator j= Aeval;
    j++;
    CFList bufEval;
    bufEval.append (j.getItem());
    j++;
    int liftBoundsLength= Aeval.getLast().level() - 1;
    for (int i= 2; i <= liftBoundsLength && j.hasItem(); i++, j++)
    {
      earlySuccess= false;
      result.insert (LC (bufEval.getFirst(), 1));
      bufEval.append (j.getItem());
      liftBound= liftBounds[i];
      Mat= CFMatrix (liftBounds[i], result.length() - 1);
 
      buf= j.getItem();
      if (smallFactorDeg >= liftBound)
        result= henselLift (bufEval, result, MOD, diophant, Pi, Mat,
                            liftBounds[i -  1], liftBounds[i]);
      else if (smallFactorDeg >= degree (buf) + 1)
      {
        result= henselLift (bufEval, result, MOD, diophant, Pi, Mat,
                            liftBounds[i -  1], degree (buf) + 1);
 
        if (Aeval.length() == i + 1)
        {
          if (!extension)
            earlyFactors= earlyFactorDetect
                           (buf, result, adaptedLiftBound, earlySuccess,
                            degree (buf) + 1, MOD, liftBound);
          else
            earlyFactors= extEarlyFactorDetect
                           (buf, result, adaptedLiftBound, earlySuccess,
                            info, evaluation, degree (buf) + 1, MOD, liftBound);
        }
        else
        {
          if (!extension)
            adaptedLiftBound= liftBoundAdaption
                                (buf, result, earlySuccess, degree (buf)
                                 + 1,  MOD, liftBound);
          else
            adaptedLiftBound= extLiftBoundAdaption
                                (buf, result, earlySuccess, info, evaluation,
                                 degree (buf) + 1, MOD, liftBound);
        }
 
        if (!earlySuccess)
        {
          result.insert (LC (buf, 1));
          liftBounds[i]= adaptedLiftBound;
          liftBound= adaptedLiftBound;
          henselLiftResume (buf, result, degree (buf) + 1, liftBound,
                            Pi, diophant, Mat, MOD);
        }
        else
        {
          liftBounds[i]= adaptedLiftBound;
        }
      }
      else if (smallFactorDeg < degree (buf) + 1)
      {
        result= henselLift (bufEval, result, MOD, diophant, Pi, Mat,
                            liftBounds[i -  1], smallFactorDeg);
 
        if (Aeval.length() == i + 1)
        {
          if (!extension)
            earlyFactors= earlyFactorDetect
                           (buf, result, adaptedLiftBound, earlySuccess,
                            smallFactorDeg, MOD, liftBound);
          else
            earlyFactors= extEarlyFactorDetect
                           (buf, result, adaptedLiftBound, earlySuccess,
                            info, evaluation, smallFactorDeg, MOD, liftBound);
        }
        else
        {
          if (!extension)
            adaptedLiftBound= liftBoundAdaption
                                (buf, result, earlySuccess,
                                 smallFactorDeg, MOD, liftBound);
          else
            adaptedLiftBound= extLiftBoundAdaption
                                (buf, result, earlySuccess, info, evaluation,
                                 smallFactorDeg, MOD, liftBound);
        }
 
        if (!earlySuccess)
        {
          result.insert (LC (buf, 1));
          henselLiftResume (buf, result, smallFactorDeg,
                            degree (buf) + 1, Pi, diophant, Mat, MOD);
          if (Aeval.length() == i + 1)
          {
            if (!extension)
              earlyFactors= earlyFactorDetect
                             (buf, result, adaptedLiftBound, earlySuccess,
                              degree (buf) +  1,  MOD, liftBound);
            else
              earlyFactors= extEarlyFactorDetect
                             (buf, result, adaptedLiftBound, earlySuccess,
                              info, evaluation, degree (buf) + 1, MOD,
                              liftBound);
          }
          else
          {
            if (!extension)
              adaptedLiftBound= liftBoundAdaption
                                  (buf, result, earlySuccess, degree
                                   (buf) +  1,  MOD, liftBound);
            else
              adaptedLiftBound= extLiftBoundAdaption
                                  (buf, result, earlySuccess, info, evaluation,
                                   degree (buf) + 1,  MOD, liftBound);
          }
 
          if (!earlySuccess)
          {
            result.insert (LC (buf, 1));
            liftBounds[i]= adaptedLiftBound;
            liftBound= adaptedLiftBound;
            henselLiftResume (buf, result, degree (buf) + 1, liftBound,
                              Pi, diophant, Mat, MOD);
          }
          else
            liftBounds[i]= adaptedLiftBound;
        }
        else
          liftBounds[i]= adaptedLiftBound;
      }
      MOD.append (power (Variable (i + 2), liftBounds[i]));
      bufEval.removeFirst();
    }
    bufFactors= result;
  }
  else
    bufFactors= result;
 
  if (earlySuccess)
    A= buf;
  return result;
}

LCHeuristic()

void LCHeuristic	(	CanonicalForm &	A,
		const CanonicalForm &	LCmultiplier,
		CFList &	biFactors,
		CFList *&	leadingCoeffs,
		const CFList *	oldAeval,
		int	lengthAeval,
		const CFList &	evaluation,
		const CFList &	oldBiFactors
	)

heuristic to distribute LCmultiplier onto factors based on the variables that occur in LCmultiplier and in the leading coeffs of bivariate factors

Parameters

[in,out]	A	a poly
[in,out]	LCmultiplier	divisor of LC (A,1)
[in,out]	biFactors	bivariate factors
[in,out]	leadingCoeffs	leading coeffs
[in]	oldAeval	bivariate factors wrt. different second vars
[in]	lengthAeval	length of oldAeval
[in]	evaluation	evaluation point
[in]	oldBiFactors	bivariate factors without LCmultiplier distributed on them

Definition at line 2614 of file facFqFactorize.cc.

{
  CFListIterator iter, iter2;
  int index;
  Variable xx;
  CFList vars1;
  CFFList sqrfMultiplier= sqrFree (LCmultiplier);
  if (sqrfMultiplier.getFirst().factor().inCoeffDomain())
    sqrfMultiplier.removeFirst();
  sqrfMultiplier= sortCFFListByNumOfVars (sqrfMultiplier);
  xx= Variable (2);
  for (iter= oldBiFactors; iter.hasItem(); iter++)
    vars1.append (power (xx, degree (LC (iter.getItem(),1), xx)));
  for (int i= 0; i < lengthAeval; i++)
  {
    if (oldAeval[i].isEmpty())
      continue;
    xx= oldAeval[i].getFirst().mvar();
    iter2= vars1;
    for (iter= oldAeval[i]; iter.hasItem(); iter++, iter2++)
      iter2.getItem() *= power (xx, degree (LC (iter.getItem(),1), xx));
  }
  CanonicalForm tmp, quot1, quot2, quot3;
  iter2= vars1;
  for (iter= leadingCoeffs[lengthAeval-1]; iter.hasItem(); iter++, iter2++)
  {
    tmp= iter.getItem()/LCmultiplier;
    for (int i=1; i <= tmp.level(); i++)
    {
      if (degree (tmp,i) > 0 && (degree (iter2.getItem(),i) > degree (tmp,i)))
        iter2.getItem() /= power (Variable (i), degree (tmp,i));
    }
  }
  int multi;
  for (CFFListIterator ii= sqrfMultiplier; ii.hasItem(); ii++)
  {
    multi= 0;
    for (iter= vars1; iter.hasItem(); iter++)
    {
      tmp= iter.getItem();
      while (fdivides (myGetVars (ii.getItem().factor()), tmp))
      {
        multi++;
        tmp /= myGetVars (ii.getItem().factor());
      }
    }
    if (multi == ii.getItem().exp())
    {
      index= 1;
      for (iter= vars1; iter.hasItem(); iter++, index++)
      {
        while (fdivides (myGetVars (ii.getItem().factor()), iter.getItem()))
        {
          int index2= 1;
          for (iter2= leadingCoeffs[lengthAeval-1]; iter2.hasItem();iter2++,
                                                                    index2++)
          {
            if (index2 == index)
              continue;
            else
            {
              tmp= ii.getItem().factor();
              if (fdivides (tmp, iter2.getItem(), quot1))
              {
                CFListIterator iter3= evaluation;
                for (int jj= A.level(); jj > 2; jj--, iter3++)
                  tmp= tmp (iter3.getItem(), jj);
                if (!tmp.inCoeffDomain())
                {
                  int index3= 1;
                  for (iter3= biFactors; iter3.hasItem(); iter3++, index3++)
                  {
                    if (index3 == index2)
                    {
                      if (fdivides (tmp, iter3.getItem(), quot2))
                      {
                        if (fdivides (ii.getItem().factor(), A, quot3))
                        {
                          A               = quot3;
                          iter2.getItem() = quot2;
                          iter3.getItem() = quot3;
                          iter3.getItem() /= Lc (iter3.getItem());
                          break;
                        }
                      }
                    }
                  }
                }
              }
            }
          }
          iter.getItem() /= getVars (ii.getItem().factor());
        }
      }
    }
    else
    {
      index= 1;
      for (iter= vars1; iter.hasItem(); iter++, index++)
      {
        if (!fdivides (myGetVars (ii.getItem().factor()), iter.getItem()))
        {
          int index2= 1;
          for (iter2= leadingCoeffs[lengthAeval-1];iter2.hasItem();iter2++,
                                                                    index2++)
          {
            if (index2 == index)
            {
              tmp= power (ii.getItem().factor(), ii.getItem().exp());
              if (fdivides (tmp, A, quot1))
              {
                if (fdivides (tmp, iter2.getItem()))
                {
                  CFListIterator iter3= evaluation;
                  for (int jj= A.level(); jj > 2; jj--, iter3++)
                    tmp= tmp (iter3.getItem(), jj);
                  if (!tmp.inCoeffDomain())
                  {
                    int index3= 1;
                    for (iter3= biFactors; iter3.hasItem(); iter3++, index3++)
                    {
                      if (index3 == index2)
                      {
                        if (fdivides (tmp, iter3.getItem(), quot3))
                        {
                          A               =  quot1;
                          iter2.getItem() =  quot2;
                          iter3.getItem() =  quot3;
                          iter3.getItem() /= Lc (iter3.getItem());
                          break;
                        }
                      }
                    }
                  }
                }
              }
            }
          }
        }
      }
    }
  }
}

LCHeuristic2()

void LCHeuristic2	(	const CanonicalForm &	LCmultiplier,
		const CFList &	factors,
		CFList &	leadingCoeffs,
		CFList &	contents,
		CFList &	LCs,
		bool &	foundTrueMultiplier
	)

heuristic to distribute LCmultiplier onto factors based on the contents of factors. factors are assumed to come from LucksWangSparseHeuristic. If not successful contents will contain the content of each element of factors and LCs will contain the LC of each element of factors divided by its content

Parameters

[in]	LCmultiplier	divisor of LC (A,1)
[in]	factors	result of LucksWangSparseHeuristic
[in,out]	leadingCoeffs	leading coeffs
[in,out]	contents	content of factors
[in,out]	LCs	LC of factors divided by content of factors
[in,out]	foundTrueMultiplier	success?

Definition at line 2778 of file facFqFactorize.cc.

{
  CanonicalForm cont;
  int index= 1;
  CFListIterator iter2;
  for (CFListIterator iter= factors; iter.hasItem(); iter++, index++)
  {
    cont= content (iter.getItem(), 1);
    cont= gcd (cont, LCmultiplier);
    contents.append (cont);
    if (cont.inCoeffDomain()) // trivial content->LCmultiplier needs to go there
    {
      foundTrueMultiplier= true;
      int index2= 1;
      for (iter2= leadingCoeffs; iter2.hasItem(); iter2++, index2++)
      {
        if (index2 == index)
          continue;
        iter2.getItem() /= LCmultiplier;
      }
      break;
    }
    else
      LCs.append (LC (iter.getItem()/cont, 1));
  }
}

LCHeuristic3()

void LCHeuristic3	(	const CanonicalForm &	LCmultiplier,
		const CFList &	factors,
		const CFList &	oldBiFactors,
		const CFList &	contents,
		const CFList *	oldAeval,
		CanonicalForm &	A,
		CFList *&	leadingCoeffs,
		int	lengthAeval,
		bool &	foundMultiplier
	)

heuristic to remove LCmultiplier from a factor based on the contents of factors. factors are assumed to come from LucksWangSparseHeuristic.

Parameters

[in]	LCmultiplier	divisor of LC (A,1)
[in]	factors	result of LucksWangSparseHeuristic
[in]	oldBiFactors	bivariate factors without LCmultiplier distributed on them
[in]	contents	content of factors
[in]	oldAeval	bivariate factors wrt. different second vars
[in,out]	A	poly
[in,out]	leadingCoeffs	leading coeffs
[in]	lengthAeval	length of oldAeval
[in,out]	foundMultiplier	success?

Definition at line 2808 of file facFqFactorize.cc.

{
  int index= 1;
  CFListIterator iter, iter2= factors;
  for (iter= contents; iter.hasItem(); iter++, iter2++, index++)
  {
    if (fdivides (iter.getItem(), LCmultiplier))
    {
      if ((LCmultiplier/iter.getItem()).inCoeffDomain() &&
          !isOnlyLeadingCoeff(iter2.getItem())) //content divides LCmultiplier completely and factor consists of more terms than just the leading coeff
      {
        Variable xx= Variable (2);
        CanonicalForm vars;
        vars= power (xx, degree (LC (getItem(oldBiFactors, index),1),
                                  xx));
        for (int i= 0; i < lengthAeval; i++)
        {
          if (oldAeval[i].isEmpty())
            continue;
          xx= oldAeval[i].getFirst().mvar();
          vars *= power (xx, degree (LC (getItem(oldAeval[i], index),1),
                                      xx));
        }
        if (vars.level() <= 2)
        {
          int index2= 1;
          for (CFListIterator iter3= leadingCoeffs[lengthAeval-1];
                iter3.hasItem(); iter3++, index2++)
          {
            if (index2 == index)
            {
              iter3.getItem() /= LCmultiplier;
              break;
            }
          }
          A /= LCmultiplier;
          foundMultiplier= true;
          iter.getItem()= 1;
        }
      }
    }
  }
}

LCHeuristic4()

void LCHeuristic4	(	const CFList &	oldBiFactors,
		const CFList *	oldAeval,
		const CFList &	contents,
		const CFList &	factors,
		const CanonicalForm &	testVars,
		int	lengthAeval,
		CFList *&	leadingCoeffs,
		CanonicalForm &	A,
		CanonicalForm &	LCmultiplier,
		bool &	foundMultiplier
	)

heuristic to remove factors of LCmultiplier from factors. More precisely checks if elements of contents divide LCmultiplier. Assumes LCHeuristic3 is run before it and was successful.

Parameters

[in]	oldBiFactors	bivariate factors without LCmultiplier distributed on them
[in]	oldAeval	bivariate factors wrt. different second vars
[in]	contents	content of factors
[in]	factors	result of LucksWangSparseHeuristic
[in]	testVars	product of second vars that occur among oldAeval
[in]	lengthAeval	length of oldAeval
[in,out]	leadingCoeffs	leading coeffs
[in,out]	A	poly
[in,out]	LCmultiplier	divisor of LC (A,1)
[in]	foundMultiplier	success?

Definition at line 2856 of file facFqFactorize.cc.

{
  int index=1;
  CFListIterator iter, iter2= factors;
  for (iter= contents; iter.hasItem(); iter++, iter2++, index++)
  {
    if (!iter.getItem().isOne() &&
        fdivides (iter.getItem(), LCmultiplier))
    {
      if (!isOnlyLeadingCoeff (iter2.getItem())) // factor is more than just leading coeff
      {
        int index2= 1;
        for (iter2= leadingCoeffs[lengthAeval-1]; iter2.hasItem();
              iter2++, index2++)
        {
          if (index2 == index)
          {
            iter2.getItem() /= iter.getItem();
            foundMultiplier= true;
            break;
          }
        }
        A /= iter.getItem();
        LCmultiplier /= iter.getItem();
        iter.getItem()= 1;
      }
      else if (fdivides (getVars (LCmultiplier), testVars))//factor consists of just leading coeff
      {
        Variable xx= Variable (2);
        CanonicalForm vars;
        vars= power (xx, degree (LC (getItem(oldBiFactors, index),1),
                                  xx));
        for (int i= 0; i < lengthAeval; i++)
        {
          if (oldAeval[i].isEmpty())
            continue;
          xx= oldAeval[i].getFirst().mvar();
          vars *= power (xx, degree (LC (getItem(oldAeval[i], index),1),
                                      xx));
        }
        if (myGetVars(content(getItem(leadingCoeffs[lengthAeval-1],index),1))
            /myGetVars (LCmultiplier) == vars)
        {
          int index2= 1;
          for (iter2= leadingCoeffs[lengthAeval-1]; iter2.hasItem();
                iter2++, index2++)
          {
            if (index2 == index)
            {
              iter2.getItem() /= LCmultiplier;
              foundMultiplier= true;
              break;
            }
          }
          A /= LCmultiplier;
          iter.getItem()= 1;
        }
      }
    }
  }
}

LCHeuristicCheck()

void LCHeuristicCheck	(	const CFList &	LCs,
		const CFList &	contents,
		CanonicalForm &	A,
		const CanonicalForm &	oldA,
		CFList &	leadingCoeffs,
		bool &	foundTrueMultiplier
	)

checks if prod(LCs)==LC (oldA,1) and if so divides elements of leadingCoeffs by elements in contents, sets A to oldA and sets foundTrueMultiplier to true

Parameters

[in]	LCs	leading coeffs computed
[in]	contents	content of factors
[in,out]	A	oldA*LCmultiplier^m
[in]	oldA	some poly
[in,out]	leadingCoeffs	leading coefficients
[in,out]	foundTrueMultiplier	success?

Definition at line 2762 of file facFqFactorize.cc.

{
  CanonicalForm pLCs= prod (LCs);
  if (fdivides (pLCs, LC (oldA,1)) && (LC(oldA,1)/pLCs).inCoeffDomain()) // check if the product of the lead coeffs of the primitive factors equals the lead coeff of the old A
  {
    A= oldA;
    CFListIterator iter2= leadingCoeffs;
    for (CFListIterator iter= contents; iter.hasItem(); iter++, iter2++)
      iter2.getItem() /= iter.getItem();
    foundTrueMultiplier= true;
  }
}

lcmContent()

CanonicalForm lcmContent	(	const CanonicalForm &	A,
		CFList &	contentAi
	)

compute the LCM of the contents of A wrt to each variable occuring in A.

Returns

lcmContent returns the LCM of the contents of A wrt to each variable occuring in A.

Parameters

[in]	A	a compressed multivariate poly
[in,out]	contentAi	an empty list, returns a list of the contents of A wrt to each variable occuring in A starting from A.mvar().

Definition at line 965 of file facFqFactorize.cc.

{
  int i= A.level();
  CanonicalForm buf= A;
  contentAi.append (content (buf, i));
  buf /= contentAi.getLast();
  contentAi.append (content (buf, i - 1));
  CanonicalForm result= lcm (contentAi.getFirst(), contentAi.getLast());
  for (i= i - 2; i > 0; i--)
  {
    contentAi.append (content (buf, i));
    buf /= contentAi.getLast();
    result= lcm (result, contentAi.getLast());
  }
  return result;
}

leadingCoeffReconstruction()

CFList leadingCoeffReconstruction	(	const CanonicalForm &	F,
		const CFList &	factors,
		const CFList &	M
	)

obtain factors of F by reconstructing their leading coeffs

Returns

returns the reconstructed factors

See also

factorRecombination()

Parameters

[in]	F	poly to be factored
[in]	factors	factors of f monic wrt Variable (1)
[in]	M	a list of powers of Variables

liftBoundAdaption()

int liftBoundAdaption	(	const CanonicalForm &	F,
		const CFList &	factors,
		bool &	success,
		const int	deg,
		const CFList &	MOD,
		const int	bound
	)

Lift bound adaption. Essentially an early factor detection but only the lift bound is adapted.

Returns

liftBoundAdaption returns an adapted lift bound.

See also

earlyFactorDetect(), earlyFactorDetection()

Parameters

[in]	F	a poly
[in]	factors	list of list of lifted factors that are monic wrt Variable (1)
[in,out]	success	indicates that no further lifting is necessary
[in]	deg	stage of Hensel lifting
[in]	MOD	a list of powers of Variables
[in]	bound	initial lift bound

Definition at line 447 of file facFqFactorize.cc.

{
  int adaptedLiftBound= 0;
  CanonicalForm buf= F;
  Variable y= F.mvar();
  Variable x= Variable (1);
  CanonicalForm LCBuf= LC (buf, x);
  CanonicalForm g, quot;
  CFList M= MOD;
  M.append (power (y, deg));
  int d= bound;
  int e= 0;
  int nBuf;
  for (CFListIterator i= factors; i.hasItem(); i++)
  {
    g= mulMod (i.getItem(), LCBuf, M);
    g /= myContent (g);
    if (fdivides (g, buf, quot))
    {
      nBuf= degree (g, y) + degree (LC (g, 1), y);
      d -= nBuf;
      e= tmax (e, nBuf);
      buf= quot;
      LCBuf= LC (buf, x);
    }
  }
  adaptedLiftBound= d;
 
  if (adaptedLiftBound < deg)
  {
    if (adaptedLiftBound < degree (F) + 1)
    {
      if (d == 1)
      {
        if (e + 1 > deg)
        {
          adaptedLiftBound= deg;
          success= false;
        }
        else
        {
          success= true;
          if (e + 1 < degree (F) + 1)
            adaptedLiftBound= deg;
          else
            adaptedLiftBound= e + 1;
        }
      }
      else
      {
        success= true;
        adaptedLiftBound= deg;
      }
    }
    else
    {
      success= true;
    }
  }
  return adaptedLiftBound;
}

myCompress()

CanonicalForm myCompress	(	const CanonicalForm &	F,
		CFMap &	N
	)

compress a polynomial s.t. 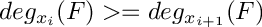and no gaps between the variables occur

Returns

a compressed poly with the above properties

Parameters

[in]	F	a poly
[in,out]	N	a map to decompress

Definition at line 133 of file facFqFactorize.cc.

{
  int n= F.level();
  int * degsf= NEW_ARRAY(int,n + 1);
  int ** swap= new int* [n + 1];
  for (int i= 0; i <= n; i++)
  {
    degsf[i]= 0;
    swap [i]= new int [3];
    swap [i] [0]= 0;
    swap [i] [1]= 0;
    swap [i] [2]= 0;
  }
  int i= 1;
  n= 1;
  degsf= degrees (F, degsf);
 
  CanonicalForm result= F;
  while ( i <= F.level() )
  {
    while( degsf[i] == 0 ) i++;
    swap[n][0]= i;
    swap[n][1]= size (LC (F,i));
    swap[n][2]= degsf [i];
    if (i != n)
      result= swapvar (result, Variable (n), Variable(i));
    n++; i++;
  }
 
  int buf1, buf2, buf3;
  n--;
 
  for (i= 1; i < n; i++)
  {
    for (int j= 1; j < n - i + 1; j++)
    {
      if (swap[j][1] > swap[j + 1][1])
      {
        buf1= swap [j + 1] [0];
        buf2= swap [j + 1] [1];
        buf3= swap [j + 1] [2];
        swap[j + 1] [0]= swap[j] [0];
        swap[j + 1] [1]= swap[j] [1];
        swap[j + 1] [2]= swap[j] [2];
        swap[j][0]= buf1;
        swap[j][1]= buf2;
        swap[j][2]= buf3;
        result= swapvar (result, Variable (j + 1), Variable (j));
      }
      else if (swap[j][1] == swap[j + 1][1] && swap[j][2] < swap[j + 1][2])
      {
        buf1= swap [j + 1] [0];
        buf2= swap [j + 1] [1];
        buf3= swap [j + 1] [2];
        swap[j + 1] [0]= swap[j] [0];
        swap[j + 1] [1]= swap[j] [1];
        swap[j + 1] [2]= swap[j] [2];
        swap[j][0]= buf1;
        swap[j][1]= buf2;
        swap[j][2]= buf3;
        result= swapvar (result, Variable (j + 1), Variable (j));
      }
    }
  }
 
  for (i= n; i > 0; i--)
  {
    if (i != swap[i] [0])
      N.newpair (Variable (i), Variable (swap[i] [0]));
  }
 
  for (i= F.level(); i >=0 ; i--)
    delete [] swap[i];
  delete [] swap;
 
  DELETE_ARRAY(degsf);
 
  return result;
}

precomputeLeadingCoeff()

CFList precomputeLeadingCoeff	(	const CanonicalForm &	LCF,
		const CFList &	LCFFactors,
		const Variable &	alpha,
		const CFList &	evaluation,
		CFList *&	differentSecondVarLCs,
		int	lSecondVarLCs,
		Variable &	y
	)

computes a list l of length length(LCFFactors)+1 of polynomials such that prod (l)=LCF, note that the first entry of l may be non constant. Intended to be used to precompute coefficients of a polynomial f from its bivariate factorizations.

Returns

see above

Parameters

[in]	LCF	a multivariate poly
[in]	LCFFactors	a list of univariate factors of LCF of level 2
[in]	alpha	algebraic var.
[in]	evaluation	an evaluation point having lSecondVarLCs+1 components
[in]	differentSecondVarLCs	LCs of factors of f wrt different second variables
[in]	lSecondVarLCs	length of the above
[in,out]	y	if y.level() is not 1 on output the second variable has been changed to y

Definition at line 1478 of file facFqFactorize.cc.

{
  y= Variable (1);
  if (LCF.inCoeffDomain())
  {
    CFList result;
    for (int i= 1; i <= LCFFactors.length() + 1; i++)
      result.append (1);
    return result;
  }
 
  CFMap N, M;
  CFArray dummy= CFArray (2);
  dummy [0]= LCF;
  dummy [1]= Variable (2);
  compress (dummy, M, N);
  CanonicalForm F= M (LCF);
  if (LCF.isUnivariate())
  {
    CFList result;
    int LCFLevel= LCF.level();
    bool found= false;
    if (LCFLevel == 2)
    {
    //bivariate leading coefficients are already the true leading coefficients
      result= LCFFactors;
      found= true;
    }
    else
    {
      CFListIterator j;
      for (int i= 0; i < lSecondVarLCs; i++)
      {
        for (j= differentSecondVarLCs[i]; j.hasItem(); j++)
        {
          if (j.getItem().level() == LCFLevel)
          {
            found= true;
            break;
          }
        }
        if (found)
        {
          result= differentSecondVarLCs [i];
          break;
        }
      }
      if (!found)
        result= LCFFactors;
    }
    if (found)
      result.insert (Lc (LCF));
    else
      result.insert (LCF);
 
    return result;
  }
 
  CFList factors= LCFFactors;
 
  for (CFListIterator i= factors; i.hasItem(); i++)
    i.getItem()= M (i.getItem());
 
  CanonicalForm sqrfPartF;
  CFFList * bufSqrfFactors= new CFFList [factors.length()];
  CFList evalSqrfPartF, bufFactors;
  CFArray evalPoint= CFArray (evaluation.length() - 1);
  CFArray buf= CFArray (evaluation.length());
  CFArray swap= CFArray (evaluation.length());
  CFListIterator iter= evaluation;
  CanonicalForm vars=getVars (LCF)*Variable (2);
  for (int i= evaluation.length() +1; i > 1; i--, iter++)
  {
    buf[i-2]=iter.getItem();
    if (degree (vars, i) > 0)
      swap[M(Variable (i)).level()-1]=buf[i-2];
  }
  buf= swap;
  for (int i= 0; i < evaluation.length() - 1; i++)
    evalPoint[i]= buf[i+1];
 
  int pass= testFactors (F, factors, alpha, sqrfPartF,
                         bufFactors, bufSqrfFactors, evalSqrfPartF, evalPoint);
 
  bool foundDifferent= false;
  Variable z, x= y;
  int j= 0;
  if (!pass)
  {
    int lev= 0;
    // LCF is non-constant here
    CFList bufBufFactors;
    CanonicalForm bufF;
    for (int i= 0; i < lSecondVarLCs; i++)
    {
      if (!differentSecondVarLCs [i].isEmpty())
      {
        bool allConstant= true;
        for (iter= differentSecondVarLCs[i]; iter.hasItem(); iter++)
        {
          if (!iter.getItem().inCoeffDomain())
          {
            allConstant= false;
            y= Variable (iter.getItem().level());
            lev= M(y).level();
          }
        }
        if (allConstant)
          continue;
 
        bufFactors= differentSecondVarLCs [i];
        for (iter= bufFactors; iter.hasItem(); iter++)
          iter.getItem()= swapvar (iter.getItem(), x, y);
        bufF= F;
        z= Variable (lev);
        bufF= swapvar (bufF, x, z);
        bufBufFactors= bufFactors;
        evalPoint= CFArray (evaluation.length() - 1);
        for (int k= 1; k < evaluation.length(); k++)
        {
          if (N (Variable (k+1)).level() != y.level())
            evalPoint[k-1]= buf[k];
          else
            evalPoint[k-1]= buf[0];
        }
        pass= testFactors (bufF, bufBufFactors, alpha, sqrfPartF, bufFactors,
                           bufSqrfFactors, evalSqrfPartF, evalPoint);
        if (pass)
        {
          foundDifferent= true;
          F= bufF;
          CFList l= factors;
          for (iter= l; iter.hasItem(); iter++)
            iter.getItem()= swapvar (iter.getItem(), x, y);
          differentSecondVarLCs [i]= l;
          j= i;
          break;
        }
        if (!pass && i == lSecondVarLCs - 1)
        {
          CFList result;
          result.append (LCF);
          for (int j= 1; j <= factors.length(); j++)
            result.append (1);
          result= distributeContent (result, differentSecondVarLCs, lSecondVarLCs);
          y= Variable (1);
          delete [] bufSqrfFactors;
          return result;
        }
      }
    }
  }
  if (!pass)
  {
    CFList result;
    result.append (LCF);
    for (int j= 1; j <= factors.length(); j++)
      result.append (1);
    result= distributeContent (result, differentSecondVarLCs, lSecondVarLCs);
    y= Variable (1);
    delete [] bufSqrfFactors;
    return result;
  }
  else
    factors= bufFactors;
 
  bufFactors= factors;
 
  CFMap MM, NN;
  dummy [0]= sqrfPartF;
  dummy [1]= 1;
  compress (dummy, MM, NN);
  sqrfPartF= MM (sqrfPartF);
  CanonicalForm varsSqrfPartF= getVars (sqrfPartF);
  for (CFListIterator iter= factors; iter.hasItem(); iter++)
    iter.getItem()= MM (iter.getItem());
 
  CFList evaluation2;
  for (int i= 2; i <= varsSqrfPartF.level(); i++)
    evaluation2.insert (evalPoint[NN (Variable (i)).level()-2]);
 
  CFList interMedResult;
  CanonicalForm oldSqrfPartF= sqrfPartF;
  sqrfPartF= shift2Zero (sqrfPartF, evalSqrfPartF, evaluation2);
  if (factors.length() > 1)
  {
    CanonicalForm LC1= LC (oldSqrfPartF, 1);
    CFList leadingCoeffs;
    for (int i= 0; i < factors.length(); i++)
      leadingCoeffs.append (LC1);
 
    CFList LC1eval= evaluateAtEval (LC1, evaluation2, 2);
    CFList oldFactors= factors;
    for (CFListIterator i= oldFactors; i.hasItem(); i++)
      i.getItem() *= LC1eval.getFirst()/Lc (i.getItem());
 
    bool success= false;
    CanonicalForm oldSqrfPartFPowLC= oldSqrfPartF*power(LC1,factors.length()-1);
    CFList heuResult;
    if (size (oldSqrfPartFPowLC)/getNumVars (oldSqrfPartFPowLC) < 500 &&
        LucksWangSparseHeuristic (oldSqrfPartFPowLC,
                                  oldFactors, 2, leadingCoeffs, heuResult))
    {
      interMedResult= recoverFactors (oldSqrfPartF, heuResult);
      if (oldFactors.length() == interMedResult.length())
        success= true;
    }
    if (!success)
    {
      LC1= LC (evalSqrfPartF.getFirst(), 1);
 
      CFArray leadingCoeffs= CFArray (factors.length());
      for (int i= 0; i < factors.length(); i++)
        leadingCoeffs[i]= LC1;
 
      for (CFListIterator i= factors; i.hasItem(); i++)
        i.getItem() *= LC1 (0,2)/Lc (i.getItem());
      factors.insert (1);
 
      CanonicalForm
      newSqrfPartF= evalSqrfPartF.getFirst()*power (LC1, factors.length() - 2);
 
      int liftBound= degree (newSqrfPartF,2) + 1;
 
      CFMatrix M= CFMatrix (liftBound, factors.length() - 1);
      CFArray Pi;
      CFList diophant;
      nonMonicHenselLift12 (newSqrfPartF, factors, liftBound, Pi, diophant, M,
                            leadingCoeffs, false);
 
      if (sqrfPartF.level() > 2)
      {
        int* liftBounds= new int [sqrfPartF.level() - 1];
        bool noOneToOne= false;
        CFList *leadingCoeffs2= new CFList [sqrfPartF.level()-2];
        LC1= LC (evalSqrfPartF.getLast(), 1);
        CFList LCs;
        for (int i= 0; i < factors.length(); i++)
          LCs.append (LC1);
        leadingCoeffs2 [sqrfPartF.level() - 3]= LCs;
        for (int i= sqrfPartF.level() - 1; i > 2; i--)
        {
          for (CFListIterator j= LCs; j.hasItem(); j++)
            j.getItem()= j.getItem() (0, i + 1);
          leadingCoeffs2 [i - 3]= LCs;
        }
        sqrfPartF *= power (LC1, factors.length()-1);
 
        int liftBoundsLength= sqrfPartF.level() - 1;
        for (int i= 0; i < liftBoundsLength; i++)
          liftBounds [i]= degree (sqrfPartF, i + 2) + 1;
        evalSqrfPartF= evaluateAtZero (sqrfPartF);
        evalSqrfPartF.removeFirst();
        factors= nonMonicHenselLift (evalSqrfPartF, factors, leadingCoeffs2,
                 diophant, Pi, liftBounds, sqrfPartF.level() - 1, noOneToOne);
        delete [] leadingCoeffs2;
        delete [] liftBounds;
      }
      for (CFListIterator iter= factors; iter.hasItem(); iter++)
        iter.getItem()= reverseShift (iter.getItem(), evaluation2);
 
      interMedResult=
      recoverFactors (reverseShift(evalSqrfPartF.getLast(),evaluation2),
                      factors);
    }
  }
  else
  {
    CanonicalForm contF=content (oldSqrfPartF,1);
    factors= CFList (oldSqrfPartF/contF);
    interMedResult= recoverFactors (oldSqrfPartF, factors);
  }
 
  for (CFListIterator iter= interMedResult; iter.hasItem(); iter++)
    iter.getItem()= NN (iter.getItem());
 
  CFList result;
  CFFListIterator k;
  for (int i= 0; i < LCFFactors.length(); i++)
  {
    CanonicalForm tmp= 1;
    for (k= bufSqrfFactors[i]; k.hasItem(); k++)
    {
      int pos= findItem (bufFactors, k.getItem().factor());
      if (pos)
        tmp *= power (getItem (interMedResult, pos), k.getItem().exp());
    }
    result.append (tmp);
  }
 
  for (CFListIterator i= result; i.hasItem(); i++)
  {
    F /= i.getItem();
    if (foundDifferent)
      i.getItem()= swapvar (i.getItem(), x, z);
    i.getItem()= N (i.getItem());
  }
 
  if (foundDifferent)
  {
    CFList l= differentSecondVarLCs [j];
    for (CFListIterator i= l; i.hasItem(); i++)
      i.getItem()= swapvar (i.getItem(), y, z);
    differentSecondVarLCs [j]= l;
    F= swapvar (F, x, z);
  }
 
  result.insert (N (F));
 
  result= distributeContent (result, differentSecondVarLCs, lSecondVarLCs);
 
  if (!result.getFirst().inCoeffDomain())
  {
    // prepare input for recursion
    if (foundDifferent)
    {
      for (CFListIterator i= result; i.hasItem(); i++)
        i.getItem()= swapvar (i.getItem(), Variable (2), y);
      CFList l= differentSecondVarLCs [j];
      for (CFListIterator i= l; i.hasItem(); i++)
        i.getItem()= swapvar (i.getItem(), y, z);
      differentSecondVarLCs [j]= l;
    }
 
    F= result.getFirst();
    int level= 0;
    if (foundDifferent)
    {
      level= y.level() - 2;
      for (int i= y.level(); i > 1; i--)
      {
        if (degree (F,i) > 0)
        {
          if (y.level() == 3)
            level= 0;
          else
            level= i-3;
        }
      }
    }
lcretry:
    if (lSecondVarLCs - level > 0)
    {
      CFList evaluation2= evaluation;
      int j= lSecondVarLCs+2;
      CanonicalForm swap;
      CFListIterator i;
      for (i= evaluation2; i.hasItem(); i++, j--)
      {
        if (j==y.level())
        {
          swap= i.getItem();
          i.getItem()= evaluation2.getLast();
          evaluation2.removeLast();
          evaluation2.append (swap);
        }
      }
 
      CFList newLCs= differentSecondVarLCs[level];
      if (newLCs.isEmpty())
      {
        if (degree (F, level+3) > 0)
        {
          delete [] bufSqrfFactors;
          return result; //TODO handle this case
        }
        level=level+1;
        goto lcretry;
      }
      i= newLCs;
      CFListIterator iter= result;
      iter++;
      CanonicalForm quot;
      for (;iter.hasItem(); iter++, i++)
      {
        swap= iter.getItem();
        if (degree (swap, level+3) > 0)
        {
          int count= evaluation.length()+1;
          for (CFListIterator iter2= evaluation2; iter2.hasItem(); iter2++,
                                                                    count--)
          {
            if (count != level+3)
              swap= swap (iter2.getItem(), count);
          }
          if (fdivides (swap, i.getItem(), quot))
            i.getItem()= quot;
        }
      }
      CFList * differentSecondVarLCs2= new CFList [lSecondVarLCs - level - 1];
      for (int j= level+1; j < lSecondVarLCs; j++)
      {
        if (degree (F, j+3) > 0)
        {
          if (!differentSecondVarLCs[j].isEmpty())
          {
            differentSecondVarLCs2[j - level - 1]= differentSecondVarLCs[j];
            i= differentSecondVarLCs2[j-level - 1];
            iter=result;
            iter++;
            for (;iter.hasItem(); iter++, i++)
            {
              swap= iter.getItem();
              if (degree (swap, j+3) > 0)
              {
                int count= evaluation.length()+1;
                for (CFListIterator iter2= evaluation2; iter2.hasItem();iter2++,
                                                                        count--)
                {
                  if (count != j+3)
                    swap= swap (iter2.getItem(), count);
                }
                if (fdivides (swap, i.getItem(), quot))
                  i.getItem()= quot;
              }
            }
          }
        }
      }
 
      for (int j= 0; j < level+1; j++)
        evaluation2.removeLast();
      Variable dummyvar= Variable (1);
 
      CanonicalForm newLCF= result.getFirst();
      newLCF=swapvar (newLCF, Variable (2), Variable (level+3));
      for (i=newLCs; i.hasItem(); i++)
        i.getItem()= swapvar (i.getItem(), Variable (2), Variable (level+3));
      for (int j= 1; j < lSecondVarLCs-level;j++)
      {
        for (i= differentSecondVarLCs2[j-1]; i.hasItem(); i++)
          i.getItem()= swapvar (i.getItem(), Variable (2+j),
                                             Variable (level+3+j));
        newLCF= swapvar (newLCF, Variable (2+j), Variable (level+3+j));
      }
 
      CFList recursiveResult=
      precomputeLeadingCoeff (newLCF, newLCs, alpha, evaluation2,
                              differentSecondVarLCs2, lSecondVarLCs - level - 1,
                              dummyvar);
 
      if (dummyvar.level() != 1)
      {
        for (i= recursiveResult; i.hasItem(); i++)
          i.getItem()= swapvar (i.getItem(), Variable (2), dummyvar);
      }
      for (i= recursiveResult; i.hasItem(); i++)
      {
        for (int j= lSecondVarLCs-level-1; j > 0; j--)
          i.getItem()=swapvar (i.getItem(), Variable (2+j),
                                      Variable (level+3+j));
        i.getItem()= swapvar (i.getItem(), Variable (2), Variable (level+3));
      }
 
      if (recursiveResult.getFirst() == result.getFirst())
      {
        delete [] bufSqrfFactors;
        delete [] differentSecondVarLCs2;
        return result;
      }
      else
      {
        iter=recursiveResult;
        i= result;
        i.getItem()= iter.getItem();
        i++;
        iter++;
        for (; i.hasItem(); i++, iter++)
          i.getItem() *= iter.getItem();
        delete [] differentSecondVarLCs2;
      }
    }
  }
  else
    y= Variable (1);
 
  delete [] bufSqrfFactors;
 
  return result;
}

prepareLeadingCoeffs()

void prepareLeadingCoeffs	(	CFList *&	LCs,
		CanonicalForm &	A,
		CFList &	Aeval,
		int	n,
		const CFList &	leadingCoeffs,
		const CFList &	biFactors,
		const CFList &	evaluation
	)

normalize precomputed leading coefficients such that leading coefficients evaluated at evaluation in K^(n-2) equal the leading coeffs wrt Variable(1) of bivariate factors and change A and Aeval accordingly

Parameters

[in,out]	LCs
[in,out]	A
[in,out]	Aeval
[in]	n	level of poly to be factored
[in]	leadingCoeffs	precomputed leading coeffs
[in]	biFactors	bivariate factors
[in]	evaluation	evaluation point

Definition at line 2381 of file facFqFactorize.cc.

{
  CFList l= leadingCoeffs;
  LCs [n-3]= l;
  CFListIterator j;
  CFListIterator iter= evaluation;
  for (int i= n - 1; i > 2; i--, iter++)
  {
    for (j= l; j.hasItem(); j++)
      j.getItem()= j.getItem() (iter.getItem(), i + 1);
    LCs [i - 3]= l;
  }
  l= LCs [0];
  for (CFListIterator i= l; i.hasItem(); i++)
    i.getItem()= i.getItem() (iter.getItem(), 3);
  CFListIterator ii= biFactors;
  CFList normalizeFactor;
  for (CFListIterator i= l; i.hasItem(); i++, ii++)
    normalizeFactor.append (Lc (LC (ii.getItem(), 1))/Lc (i.getItem()));
  for (int i= 0; i < n-2; i++)
  {
    ii= normalizeFactor;
    for (j= LCs [i]; j.hasItem(); j++, ii++)
      j.getItem() *= ii.getItem();
  }
 
  Aeval= evaluateAtEval (A, evaluation, 2);
 
  CanonicalForm hh= 1/Lc (Aeval.getFirst());
 
  for (iter= Aeval; iter.hasItem(); iter++)
    iter.getItem() *= hh;
 
  A *= hh;
}

recombination()

CFList recombination	(	const CFList &	factors1,
		const CFList &	factors2,
		int	s,
		int	thres,
		const CanonicalForm &	evalPoint,
		const Variable &	x
	)

recombination of bivariate factors factors1 s. t. the result evaluated at evalPoint coincides with factors2

Parameters

[in]	factors1	list of bivariate factors
[in]	factors2	list univariate factors
[in]	s	algorithm starts checking subsets of size s
[in]	thres	threshold for the size of subsets which are checked
[in]	evalPoint	evaluation point
[in]	x	second variable of bivariate factors

Definition at line 2113 of file facFqFactorize.cc.

{
  CFList T, S;
 
  T= factors1;
  CFList result;
  CanonicalForm buf;
  int * v= new int [T.length()];
  for (int i= 0; i < T.length(); i++)
    v[i]= 0;
  bool nosubset= false;
  CFArray TT;
  TT= copy (factors1);
  int recombinations= 0;
  while (T.length() >= 2*s && s <= thres)
  {
    while (nosubset == false)
    {
      if (T.length() == s)
      {
        delete [] v;
        if (recombinations == factors2.length() - 1)
          result.append (prod (T));
        else
          result= Union (result, T);
        return result;
      }
      S= subset (v, s, TT, nosubset);
      if (nosubset) break;
      buf= prodEval (S, evalPoint, x);
      buf /= Lc (buf);
      if (find (factors2, buf))
      {
        recombinations++;
        T= Difference (T, S);
        result.append (prod (S));
        TT= copy (T);
        indexUpdate (v, s, T.length(), nosubset);
        if (nosubset) break;
      }
    }
    s++;
    if (T.length() < 2*s || T.length() == s)
    {
      if (recombinations == factors2.length() - 1)
        result.append (prod (T));
      else
        result= Union (result, T);
      delete [] v;
      return result;
    }
    for (int i= 0; i < T.length(); i++)
      v[i]= 0;
    nosubset= false;
  }
 
  delete [] v;
  if (T.length() < 2*s)
  {
    result= Union (result, T);
    return result;
  }
 
  return result;
}

refineBiFactors()

void refineBiFactors	(	const CanonicalForm &	A,
		CFList &	biFactors,
		CFList *const &	factors,
		const CFList &	evaluation,
		int	minFactorsLength
	)

refine a bivariate factorization of A with l factors to one with minFactorsLength if possible

Parameters

[in]	A	some poly
[in,out]	biFactors	list of bivariate to be refined, returns refined factors
[in]	factors	list of bivariate factorizations of A wrt different second variables
[in]	evaluation	the evaluation point
[in]	minFactorsLength	the minimal number of factors

Definition at line 2334 of file facFqFactorize.cc.

{
  CFListIterator iter, iter2;
  CanonicalForm evalPoint;
  int i;
  Variable v;
  Variable y= Variable (2);
  CFList list;
  bool leaveLoop= false;
  for (int j= 0; j < A.level() - 2; j++)
  {
    if (Aeval[j].length() == minFactorsLength)
    {
      i= A.level();
 
      for (iter= evaluation; iter.hasItem(); iter++, i--)
      {
        for (iter2= Aeval[j]; iter2.hasItem(); iter2++)
        {
          if (i == iter2.getItem().level())
          {
            evalPoint= iter.getItem();
            leaveLoop= true;
            break;
          }
        }
        if (leaveLoop)
        {
          leaveLoop= false;
          break;
        }
      }
 
      v= Variable (i);
      list= buildUniFactors (Aeval[j], evalPoint, v);
 
      biFactors= recombination (biFactors, list, 1,
                                biFactors.length() - list.length() + 1,
                                evaluation.getLast(), y);
      return;
    }
  }
}

sortByUniFactors()

void sortByUniFactors	(	CFList *&	Aeval,
		int	AevalLength,
		CFList &	uniFactors,
		CFList &	biFactors,
		const CFList &	evaluation
	)

sort bivariate factors in Aeval such that their corresponding univariate factors coincide with uniFactors, uniFactors and biFactors may get recombined if necessary

Parameters

[in,out]	Aeval	array of bivariate factors
[in]	AevalLength	length of Aeval
[in,out]	uniFactors	univariate factors
[in,out]	biFactors	bivariate factors
[in]	evaluation	evaluation point

Definition at line 2250 of file facFqFactorize.cc.

{
  CanonicalForm evalPoint;
  int i;
  CFListIterator iter, iter2;
  Variable v;
  CFList LCs, buf;
  CFArray l;
  int pos, index, checklength;
  bool leaveLoop=false;
recurse:
  for (int j= 0; j < AevalLength; j++)
  {
    if (!Aeval[j].isEmpty())
    {
      i= evaluation.length() + 1;
      for (iter= evaluation; iter.hasItem(); iter++, i--)
      {
        for (iter2= Aeval[j]; iter2.hasItem(); iter2++)
        {
          if (i == iter2.getItem().level())
          {
            evalPoint= iter.getItem();
            leaveLoop= true;
            break;
          }
        }
        if (leaveLoop)
        {
          leaveLoop= false;
          break;
        }
      }
 
      v= Variable (i);
      if (Aeval[j].length() > uniFactors.length())
        Aeval[j]= recombination (Aeval[j], uniFactors, 1,
                                 Aeval[j].length() - uniFactors.length() + 1,
                                 evalPoint, v);
 
      checklength= biFactors.length();
      Aeval[j]= checkOneToOne (Aeval[j], uniFactors, biFactors, evalPoint, v);
      if (checklength > biFactors.length())
      {
        uniFactors= buildUniFactors (biFactors, evaluation.getLast(),
                                     Variable (2));
        goto recurse;
      }
 
      buf= buildUniFactors (Aeval[j], evalPoint, v);
      l= CFArray (uniFactors.length());
      index= 1;
      for (iter= buf; iter.hasItem(); iter++, index++)
      {
        pos= findItem (uniFactors, iter.getItem());
        if (pos)
          l[pos-1]= getItem (Aeval[j], index);
      }
      buf= conv (l);
      Aeval [j]= buf;
 
      buf= buildUniFactors (Aeval[j], evalPoint, v);
    }
  }
}

TIMING_DEFINE_PRINT()

TIMING_DEFINE_PRINT

(

fac_fq_squarefree

)

const &

Factorization over a finite field.

Returns

multiFactorize returns a factorization of F

See also

biFactorize(), extFactorize()

Variable Documentation

info

const ExtensionInfo& info

< [in] sqrfree poly

< [in] info about extension

Definition at line 37 of file facFqFactorize.h.