facFqBivarUtil.cc File Reference

This file provides utility functions for bivariate factorization. More...

#include "config.h"
#include "timing.h"
#include "cf_map.h"
#include "cf_map_ext.h"
#include "templates/ftmpl_functions.h"
#include "ExtensionInfo.h"
#include "cf_algorithm.h"
#include "cf_factory.h"
#include "cf_util.h"
#include "imm.h"
#include "cf_iter.h"
#include "facFqBivarUtil.h"
#include "cfNewtonPolygon.h"
#include "facHensel.h"
#include "facMul.h"
#include "FLINTconvert.h"

Go to the source code of this file.

Macros
#define	slong   long

Functions
	TIMING_DEFINE_PRINT (fac_log_deriv_div) TIMING_DEFINE_PRINT(fac_log_deriv_mul) TIMING_DEFINE_PRINT(fac_log_deriv_pre) void append(CFList &factors1
void	decompress (CFList &factors, const CFMap &N)
	decompress a list of polys factors using the map N More...
void	decompress (CFFList &factors, const CFMap &N)
	as above More...
void	decompress (CFAFList &factors, const CFMap &N)
	as above More...
void	appendSwapDecompress (CFList &factors1, const CFList &factors2, const CFList &factors3, const bool swap1, const bool swap2, const CFMap &N)
	first swap Variables in factors1 if necessary, then append factors2 and factors3 on factors1 and finally decompress factors1 More...
void	swapDecompress (CFList &factors, const bool swap, const CFMap &N)
	swap Variables in factors, then decompress factors More...
static bool	GFInExtensionHelper (const CanonicalForm &F, const int number)
static bool	FqInExtensionHelper (const CanonicalForm &F, const CanonicalForm &gamma, const CanonicalForm &delta, CFList &source, CFList &dest)
bool	isInExtension (const CanonicalForm &F, const CanonicalForm &gamma, const int k, const CanonicalForm &delta, CFList &source, CFList &dest)
	tests if F is not contained in a subfield defined by gamma (Fq case) or k (GF case) More...
CanonicalForm	mapDown (const CanonicalForm &F, const ExtensionInfo &info, CFList &source, CFList &dest)
	map a poly into a subfield of the current field, no testing is performed! More...
void	appendTestMapDown (CFList &factors, const CanonicalForm &f, const ExtensionInfo &info, CFList &source, CFList &dest)
	test if g is in a subfield of the current field, if so map it down and append it to factors More...
void	appendMapDown (CFList &factors, const CanonicalForm &g, const ExtensionInfo &info, CFList &source, CFList &dest)
	map g down into a subfield of the current field and append it to factors More...
void	normalize (CFList &factors)
	normalize factors, i.e. make factors monic More...
void	normalize (CFFList &factors)
	as above More...
CFList	subset (int index[], const int &s, const CFArray &elements, bool &noSubset)
	extract a subset given by index of size s from elements, if there is no subset we have not yet considered noSubset is set to true. index encodes the next subset, e.g. if s= 3, elements= {a,b,c,d}, index= {1, 2, 4, 0}, then subset= {a,c,d}. index is of size elements.size(). More...
CFArray	copy (const CFList &list)
	write elements of list into an array More...
void	indexUpdate (int index[], const int &subsetSize, const int &setSize, bool &noSubset)
	update index More...
int	subsetDegree (const CFList &S)
	compute the sum of degrees in Variable(1) of elements in S More...
CFFList	multiplicity (CanonicalForm &F, const CFList &factors)
	determine multiplicity of the factors More...
CFArray	logarithmicDerivative (const CanonicalForm &F, const CanonicalForm &G, int l, CanonicalForm &Q)
	compute the coefficients of the logarithmic derivative of G mod Variable (2)^l over Fq More...
CFArray	logarithmicDerivative (const CanonicalForm &F, const CanonicalForm &G, int l, int oldL, const CanonicalForm &oldQ, CanonicalForm &Q)
	compute the coefficients of the logarithmic derivative of G mod Variable (2)^l over Fq with oldQ= F/G mod Variable (2)^oldL More...
void	writeInMatrix (CFMatrix &M, const CFArray &A, const int column, const int startIndex)
	write A into M starting at row startIndex More...
CFArray	getCoeffs (const CanonicalForm &F, const int k)
	extract coefficients of for where is a variable of level 1 More...
CFArray	getCoeffs (const CanonicalForm &F, const int k, const Variable &alpha)
	extract coefficients of for where is a variable of level 1 More...
CFArray	getCoeffs (const CanonicalForm &G, const int k, const int l, const int degMipo, const Variable &alpha, const CanonicalForm &evaluation, const mat_zz_p &M)
	extract coefficients of for where is a variable of level 1 More...
CFArray	getCoeffs (const CanonicalForm &G, const int k, const int l, const int degMipo, const Variable &alpha, const CanonicalForm &evaluation, const nmod_mat_t M)
	extract coefficients of for where is a variable of level 1 More...
int *	computeBounds (const CanonicalForm &F, int &n, bool &isIrreducible)
	compute bounds for logarithmic derivative as described in K. Belabas, M. van Hoeij, J. Klüners, and A. Steel, Factoring polynomials over global fields More...
int *	computeBoundsWrtDiffMainvar (const CanonicalForm &F, int &n, bool &isIrreducible)
	as above just wrt to the other variable More...
int	substituteCheck (const CanonicalForm &F, const Variable &x)
	check if a substitution x^n->x is possible More...
static int	substituteCheck (const CanonicalForm &F, const CanonicalForm &G)
int	recSubstituteCheck (const CanonicalForm &F, const int d)
int	substituteCheck (const CFList &L)
	checks if a substitution x^n->x is possible More...
void	subst (const CanonicalForm &F, CanonicalForm &A, const int d, const Variable &x)
	substitute x^d by x in F More...
CanonicalForm	reverseSubst (const CanonicalForm &F, const int d, const Variable &x)
	reverse a substitution x^d->x More...
void	reverseSubst (CFList &L, const int d, const Variable &x)
	reverse a substitution x^d->x More...

Variables
const CFList &	factors2

Detailed Description

This file provides utility functions for bivariate factorization.

Author

Martin Lee

Definition in file facFqBivarUtil.cc.

Macro Definition Documentation

slong

#define slong   long

Function Documentation

appendMapDown()

void appendMapDown	(	CFList &	factors,
		const CanonicalForm &	g,
		const ExtensionInfo &	info,
		CFList &	source,
		CFList &	dest
	)

map g down into a subfield of the current field and append it to factors

See also

mapDown(), appendTestMapDown()

Parameters

[in,out]	factors	a list of polys
[in]	g	a poly
[in]	info	information about extension
[in,out]	source

See also

mapDown()

Parameters

[in,out]

dest

See also

mapDown()

Definition at line 267 of file facFqBivarUtil.cc.

{
  int k= info.getGFDegree();
  Variable beta= info.getBeta();
  Variable alpha= info.getAlpha();
  CanonicalForm gamma= info.getGamma();
  CanonicalForm delta= info.getDelta();
  if (k > 1)
    factors.append (GFMapDown (g, k));
  else if (k == 1)
    factors.append (g);
  else if (!k && beta == Variable (1))
    factors.append (g);
  else if (!k && beta != Variable (1))
    factors.append (mapDown (g, delta, gamma, alpha, source, dest));
  return;
}

appendSwapDecompress()

void appendSwapDecompress	(	CFList &	factors1,
		const CFList &	factors2,
		const CFList &	factors3,
		const bool	swap1,
		const bool	swap2,
		const CFMap &	N
	)

first swap Variables in factors1 if necessary, then append factors2 and factors3 on factors1 and finally decompress factors1

Parameters

[in,out]	factors1	a list of polys
[in]	factors2	a list of polys
[in]	factors3	a list of polys
[in]	swap1	indicates the need to swap
[in]	swap2	indicates the need to swap
[in]	N	a map

Definition at line 70 of file facFqBivarUtil.cc.

{
  Variable x= Variable (1);
  Variable y= Variable (2);
  for (CFListIterator i= factors1; i.hasItem(); i++)
  {
    if (swap1)
    {
      if (!swap2)
        i.getItem()= swapvar (i.getItem(), x, y);
    }
    else
    {
      if (swap2)
        i.getItem()= swapvar (i.getItem(), y, x);
    }
    i.getItem()= N (i.getItem());
  }
  for (CFListIterator i= factors2; i.hasItem(); i++)
    factors1.append (N (i.getItem()));
  for (CFListIterator i= factors3; i.hasItem(); i++)
    factors1.append (N (i.getItem()));
  return;
}

appendTestMapDown()

void appendTestMapDown	(	CFList &	factors,
		const CanonicalForm &	f,
		const ExtensionInfo &	info,
		CFList &	source,
		CFList &	dest
	)

test if g is in a subfield of the current field, if so map it down and append it to factors

See also

mapDown(), isInExtension()

Parameters

[in,out]	factors	a list of polys
[in]	f	a poly
[in]	info	information about extension
[in,out]	source

See also

mapDown()

Parameters

[in,out]

dest

See also

mapDown()

Definition at line 223 of file facFqBivarUtil.cc.

{
  int k= info.getGFDegree();
  Variable beta= info.getBeta();
  Variable alpha= info.getAlpha();
  CanonicalForm delta= info.getDelta();
  CanonicalForm gamma= info.getGamma();
  CanonicalForm g= f;
  int degMipoBeta=0;
  if (!k && beta.level() == 1)
    degMipoBeta= 1;
  else if (!k && beta.level() != 1)
    degMipoBeta= degree (getMipo (beta));
  if (k > 1)
  {
    if (!isInExtension (g, gamma, k, delta, source, dest))
    {
      g= GFMapDown (g, k);
      factors.append (g);
    }
  }
  else if (k == 1)
  {
    if (!isInExtension (g, gamma, k, delta, source, dest))
      factors.append (g);
  }
  else if (!k && beta == Variable (1))
  {
    if (degree (g, alpha) < degMipoBeta)
      factors.append (g);
  }
  else if (!k && beta != Variable (1))
  {
    if (!isInExtension (g, gamma, k, delta, source, dest))
    {
      g= mapDown (g, delta, gamma, alpha, source, dest);
      factors.append (g);
    }
  }
  return;
}

computeBounds()

int * computeBounds	(	const CanonicalForm &	F,
		int &	n,
		bool &	isIrreducible
	)

compute bounds for logarithmic derivative as described in K. Belabas, M. van Hoeij, J. Klüners, and A. Steel, Factoring polynomials over global fields

Returns

computeBounds returns bounds as described above

Parameters

[in]	F	compressed bivariate polynomial
[in,out]	n	length of output
[in,out]	isIrreducible	check if poly is irreducible

Definition at line 768 of file facFqBivarUtil.cc.

{
  n= degree (F, 1);
  int* result= new int [n];
  int sizeOfNewtonPolygon;
  int** newtonPolyg= newtonPolygon (F, sizeOfNewtonPolygon);
 
  isIrreducible= false;
  if (sizeOfNewtonPolygon == 3)
  {
    bool check1=
        (newtonPolyg[0][0]==0 || newtonPolyg[1][0]==0 || newtonPolyg[2][0]==0);
    if (check1)
    {
      bool check2=
        (newtonPolyg[0][1]==0 || newtonPolyg[1][1]==0 || newtonPolyg[2][0]==0);
      if (check2)
      {
        int p=getCharacteristic();
        int d=1;
        char bufGFName='Z';
        bool GF= (CFFactory::gettype()==GaloisFieldDomain);
        if (GF)
        {
          d= getGFDegree();
          bufGFName=gf_name;
        }
        setCharacteristic(0);
        CanonicalForm tmp= gcd (newtonPolyg[0][0],newtonPolyg[0][1]);  // maybe it's better to use plain intgcd
        tmp= gcd (tmp, newtonPolyg[1][0]);
        tmp= gcd (tmp, newtonPolyg[1][1]);
        tmp= gcd (tmp, newtonPolyg[2][0]);
        tmp= gcd (tmp, newtonPolyg[2][1]);
        isIrreducible= (tmp==1);
        if (GF)
          setCharacteristic (p, d, bufGFName);
        else
          setCharacteristic(p);
      }
    }
  }
 
  int minX, minY, maxX, maxY;
  minX= newtonPolyg [0] [0];
  minY= newtonPolyg [0] [1];
  maxX= minX;
  maxY= minY;
  int indZero= 0;
  for (int i= 1; i < sizeOfNewtonPolygon; i++)
  {
    if (newtonPolyg[i][1] == 0)
    {
      if (newtonPolyg[indZero][1] == 0)
      {
        if (newtonPolyg[indZero][0] < newtonPolyg[i][0])
          indZero= i;
      }
      else
        indZero= i;
    }
    if (minX > newtonPolyg [i] [0])
      minX= newtonPolyg [i] [0];
    if (maxX < newtonPolyg [i] [0])
      maxX= newtonPolyg [i] [0];
    if (minY > newtonPolyg [i] [1])
      minY= newtonPolyg [i] [1];
    if (maxY < newtonPolyg [i] [1])
      maxY= newtonPolyg [i] [1];
  }
 
  int slopeNum, slopeDen, constTerm;
  bool negativeSlope=false;
  if (indZero != sizeOfNewtonPolygon - 1)
  {
    slopeNum= newtonPolyg[indZero+1][0]-newtonPolyg[indZero][0];
    slopeDen= newtonPolyg[indZero+1][1];
    constTerm= newtonPolyg[indZero][0];
  }
  else
  {
    slopeNum= newtonPolyg[0][0]-newtonPolyg[indZero][0];
    slopeDen= newtonPolyg[0][1];
    constTerm= newtonPolyg[indZero][0];
  }
  if (slopeNum < 0)
  {
    slopeNum= -slopeNum;
    negativeSlope= true;
  }
  int k= 0;
  int* point= new int [2];
  for (int i= 0; i < n; i++)
  {
    if (((indZero+1) < sizeOfNewtonPolygon && (i+1) > newtonPolyg[indZero+1][1])
        || ((indZero+1) >= sizeOfNewtonPolygon && (i+1) > newtonPolyg[0][1]))
    {
      if (indZero + 1 != sizeOfNewtonPolygon)
        indZero++;
      else
        indZero= 0;
      if (indZero != sizeOfNewtonPolygon - 1)
      {
        slopeNum= newtonPolyg[indZero+1][0]-newtonPolyg[indZero][0];
        slopeDen= newtonPolyg[indZero+1][1]-newtonPolyg[indZero][1];
        constTerm= newtonPolyg[indZero][0];
      }
      else
      {
        slopeNum= newtonPolyg[0][0]-newtonPolyg[indZero][0];
        slopeDen= newtonPolyg[0][1]-newtonPolyg[indZero][1];
        constTerm= newtonPolyg[indZero][0];
      }
      if (slopeNum < 0)
      {
        negativeSlope= true;
        slopeNum= - slopeNum;
        k= (int) -(((long) slopeNum*((i+1)-newtonPolyg[indZero][1])+slopeDen-1)/
                   slopeDen) + constTerm;
      }
      else
        k= (int) (((long) slopeNum*((i+1)-newtonPolyg[indZero][1])) / slopeDen)
                  + constTerm;
    }
    else
    {
      if (negativeSlope)
        k= (int) -(((long) slopeNum*((i+1)-newtonPolyg[indZero][1])+slopeDen-1)/
                   slopeDen) + constTerm;
      else
        k= (int) ((long) slopeNum*((i+1)-newtonPolyg[indZero][1])) / slopeDen
                  + constTerm;
    }
    if (i + 1 > maxY || i + 1 < minY)
    {
      result [i]= 0;
      continue;
    }
    point [0]= k;
    point [1]= i + 1;
    if (!isInPolygon (newtonPolyg, sizeOfNewtonPolygon, point) && k > 0)
      k= 0;
    result [i]= k;
  }
 
  delete [] point;
 
  for (int i= 0; i < sizeOfNewtonPolygon; i++)
    delete [] newtonPolyg[i];
  delete [] newtonPolyg;
 
  return result;
}

computeBoundsWrtDiffMainvar()

int * computeBoundsWrtDiffMainvar	(	const CanonicalForm &	F,
		int &	n,
		bool &	isIrreducible
	)

as above just wrt to the other variable

Returns

computeBounds returns bounds as described above

Parameters

[in]	F	compressed bivariate polynomial
[in,out]	n	length of output
[in,out]	isIrreducible	check if poly is irreducible

Definition at line 922 of file facFqBivarUtil.cc.

{
  n= degree (F, 2);
  int* result= new int [n];
  int sizeOfNewtonPolygon;
  int** newtonPolyg= newtonPolygon (F, sizeOfNewtonPolygon);
 
  isIrreducible= false;
  if (sizeOfNewtonPolygon == 3)
  {
    bool check1=
        (newtonPolyg[0][0]==0 || newtonPolyg[1][0]==0 || newtonPolyg[2][0]==0);
    if (check1)
    {
      bool check2=
        (newtonPolyg[0][1]==0 || newtonPolyg[1][1]==0 || newtonPolyg[2][0]==0);
      if (check2)
      {
        int p=getCharacteristic();
        int d=1;
        char bufGFName='Z';
        bool GF= (CFFactory::gettype()==GaloisFieldDomain);
        if (GF)
        {
          d= getGFDegree();
          bufGFName=gf_name;
        }
        setCharacteristic(0);
        CanonicalForm tmp= gcd (newtonPolyg[0][0],newtonPolyg[0][1]);
        tmp= gcd (tmp, newtonPolyg[1][0]);
        tmp= gcd (tmp, newtonPolyg[1][1]);
        tmp= gcd (tmp, newtonPolyg[2][0]);
        tmp= gcd (tmp, newtonPolyg[2][1]);
        isIrreducible= (tmp==1);
        if (GF)
          setCharacteristic (p, d, bufGFName);
        else
          setCharacteristic(p);
      }
    }
  }
 
  int swap;
  for (int i= 0; i < sizeOfNewtonPolygon; i++)
  {
    swap= newtonPolyg[i][1];
    newtonPolyg[i][1]=newtonPolyg[i][0];
    newtonPolyg[i][0]= swap;
  }
 
  sizeOfNewtonPolygon= polygon(newtonPolyg, sizeOfNewtonPolygon);
 
  int minX, minY, maxX, maxY;
  minX= newtonPolyg [0] [0];
  minY= newtonPolyg [0] [1];
  maxX= minX;
  maxY= minY;
  int indZero= 0;
  for (int i= 1; i < sizeOfNewtonPolygon; i++)
  {
    if (newtonPolyg[i][1] == 0)
    {
      if (newtonPolyg[indZero][1] == 0)
      {
        if (newtonPolyg[indZero][0] < newtonPolyg[i][0])
          indZero= i;
      }
      else
        indZero= i;
    }
    if (minX > newtonPolyg [i] [0])
      minX= newtonPolyg [i] [0];
    if (maxX < newtonPolyg [i] [0])
      maxX= newtonPolyg [i] [0];
    if (minY > newtonPolyg [i] [1])
      minY= newtonPolyg [i] [1];
    if (maxY < newtonPolyg [i] [1])
      maxY= newtonPolyg [i] [1];
  }
 
  int slopeNum, slopeDen, constTerm;
  bool negativeSlope=false;
  if (indZero != sizeOfNewtonPolygon - 1)
  {
    slopeNum= newtonPolyg[indZero+1][0]-newtonPolyg[indZero][0];
    slopeDen= newtonPolyg[indZero+1][1];
    constTerm= newtonPolyg[indZero][0];
  }
  else
  {
    slopeNum= newtonPolyg[0][0]-newtonPolyg[indZero][0];
    slopeDen= newtonPolyg[0][1];
    constTerm= newtonPolyg[indZero][0];
  }
  if (slopeNum < 0)
  {
    slopeNum= -slopeNum;
    negativeSlope= true;
  }
  int k= 0;
 
  int* point= new int [2];
  for (int i= 0; i < n; i++)
  {
    if (((indZero+1) < sizeOfNewtonPolygon && (i+1) > newtonPolyg[indZero+1][1])
        || ((indZero+1) >= sizeOfNewtonPolygon && (i+1) > newtonPolyg[0][1]))
    {
      if (indZero + 1 != sizeOfNewtonPolygon)
        indZero++;
      else
        indZero= 0;
      if (indZero != sizeOfNewtonPolygon - 1)
      {
        slopeNum= newtonPolyg[indZero+1][0]-newtonPolyg[indZero][0];
        slopeDen= newtonPolyg[indZero+1][1]-newtonPolyg[indZero][1];
        constTerm= newtonPolyg[indZero][0];
      }
      else
      {
        slopeNum= newtonPolyg[0][0]-newtonPolyg[indZero][0];
        slopeDen= newtonPolyg[0][1]-newtonPolyg[indZero][1];
        constTerm= newtonPolyg[indZero][0];
      }
      if (slopeNum < 0)
      {
        negativeSlope= true;
        slopeNum= - slopeNum;
        k= (int) -(((long) slopeNum*((i+1)-newtonPolyg[indZero][1])+slopeDen-1)/
                   slopeDen) + constTerm;
      }
      else
        k= (int) (((long) slopeNum*((i+1)-newtonPolyg[indZero][1])) / slopeDen)
                  + constTerm;
    }
    else
    {
      if (negativeSlope)
        k= (int) -(((long) slopeNum*((i+1)-newtonPolyg[indZero][1])+slopeDen-1)/
                   slopeDen) + constTerm;
      else
        k= (int) ((long) slopeNum*((i+1)-newtonPolyg[indZero][1])) / slopeDen
                  + constTerm;
    }
    if (i + 1 > maxY || i + 1 < minY)
    {
      result [i]= 0;
      continue;
    }
 
    point [0]= k;
    point [1]= i + 1;
    if (!isInPolygon (newtonPolyg, sizeOfNewtonPolygon, point) && k > 0)
      k= 0;
    result [i]= k;
  }
 
  delete [] point;
 
  for (int i= 0; i < sizeOfNewtonPolygon; i++)
    delete [] newtonPolyg[i];
  delete [] newtonPolyg;
 
  return result;
}

copy()

CFArray copy

(

const CFList &

list

)

write elements of list into an array

Returns

an array of polys

Parameters

[in]

list

a list of polys

Definition at line 364 of file facFqBivarUtil.cc.

{
  CFArray array= CFArray (list.length());
  int j= 0;
  for (CFListIterator i= list; i.hasItem(); i++, j++)
    array[j]= i.getItem();
  return array;
}

decompress() [1/3]

void decompress	(	CFAFList &	factors,
		const CFMap &	N
	)

as above

Parameters

[in,out]	factors	a list of factors
[in]	N	a map

Definition at line 63 of file facFqBivarUtil.cc.

{
  for (CFAFListIterator i= factors; i.hasItem(); i++)
    i.getItem()= CFAFactor (N (i.getItem().factor()), i.getItem().minpoly(),
                            i.getItem().exp());
}

decompress() [2/3]

void decompress	(	CFFList &	factors,
		const CFMap &	N
	)

as above

Parameters

[in,out]	factors	a list of factors
[in]	N	a map

Definition at line 57 of file facFqBivarUtil.cc.

{
  for (CFFListIterator i= factors; i.hasItem(); i++)
    i.getItem()= CFFactor (N (i.getItem().factor()), i.getItem().exp());
}

decompress() [3/3]

void decompress	(	CFList &	factors,
		const CFMap &	N
	)

decompress a list of polys factors using the map N

Parameters

[in,out]	factors	a list of polys
[in]	N	a map

Definition at line 51 of file facFqBivarUtil.cc.

{
  for (CFListIterator i= factors; i.hasItem(); i++)
    i.getItem()= N (i.getItem());
}

FqInExtensionHelper()

static bool FqInExtensionHelper ( const CanonicalForm &  F, const CanonicalForm &  gamma, const CanonicalForm &  delta, CFList &  source, CFList &  dest  )

inlinestatic

Definition at line 139 of file facFqBivarUtil.cc.

{
  bool result= false;
  if (F.inBaseDomain())
    return result;
  else if (F.inCoeffDomain())
  {
    if (!fdivides (gamma, F))
      return true;
    else
    {
      int pos= findItem (source, F);
      if (pos > 0)
        return false;
      Variable a;
      hasFirstAlgVar (F, a);
      int bound= ipower (getCharacteristic(), degree (getMipo (a)));
      CanonicalForm buf= 1;
      for (int i= 1; i < bound; i++)
      {
        buf *= gamma;
        if (buf == F)
        {
          source.append (buf);
          dest.append (power (delta, i));
          return false;
        }
      }
      return true;
    }
  }
  else
  {
    for (CFIterator i= F; i.hasTerms(); i++)
    {
      result= FqInExtensionHelper (i.coeff(), gamma, delta, source, dest);
      if (result == true)
        return result;
    }
  }
  return result;
}

getCoeffs() [1/4]

CFArray getCoeffs	(	const CanonicalForm &	F,
		const int	k
	)

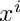
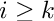
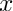
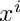
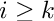
extract coefficients of for where is a variable of level 1

Returns

coefficients of for

See also

{getCoeffs (const CanonicalForm&, const int, const Variable&), getCoeffs (const CanonicalForm&, const int, const int, const int, const Variable&, const CanonicalForm&, const mat_zz_p&)}

Parameters

[in]	F	compressed bivariate poly over F_p
[in]	k	some int

Definition at line 599 of file facFqBivarUtil.cc.

{
  ASSERT (F.isUnivariate() || F.inCoeffDomain(), "univariate input expected");
  if (degree (F, 2) < k)
    return CFArray();
 
  CFArray result= CFArray (degree (F) - k + 1);
  CFIterator j= F;
  for (int i= degree (F); i >= k; i--)
  {
    if (j.exp() == i)
    {
      result [i - k]= j.coeff();
      j++;
      if (!j.hasTerms())
        return result;
    }
    else
      result[i - k]= 0;
  }
  return result;
}

getCoeffs() [2/4]

CFArray getCoeffs	(	const CanonicalForm &	F,
		const int	k,
		const Variable &	alpha
	)

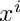
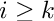
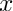
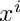
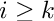
extract coefficients of for where is a variable of level 1

Returns

coefficients of for

See also

{getCoeffs (const CanonicalForm&, const int), getCoeffs (const CanonicalForm&, const int, const int, const int, const Variable&, const CanonicalForm&, const mat_zz_p&)}

Parameters

[in]	F	compressed bivariate poly over F_p(alpha)
[in]	k	some int
[in]	alpha	algebraic variable

Definition at line 622 of file facFqBivarUtil.cc.

{
  ASSERT (F.isUnivariate() || F.inCoeffDomain(), "univariate input expected");
  if (degree (F, 2) < k)
    return CFArray ();
 
  int d= degree (getMipo (alpha));
  CFArray result= CFArray ((degree (F) - k + 1)*d);
  CFIterator j= F;
  CanonicalForm buf;
  CFIterator iter;
  for (int i= degree (F); i >= k; i--)
  {
    if (j.exp() == i)
    {
      iter= j.coeff();
      for (int l= degree (j.coeff(), alpha); l >= 0; l--)
      {
        if (iter.exp() == l)
        {
          result [(i - k)*d + l]= iter.coeff();
          iter++;
          if (!iter.hasTerms())
            break;
        }
      }
      j++;
      if (!j.hasTerms())
        return result;
    }
    else
    {
      for (int l= 0; l < d; l++)
        result[(i - k)*d + l]= 0;
    }
  }
  return result;
}

getCoeffs() [3/4]

CFArray getCoeffs	(	const CanonicalForm &	F,
		const int	k,
		const int	l,
		const int	degMipo,
		const Variable &	alpha,
		const CanonicalForm &	evaluation,
		const mat_zz_p &	M
	)

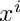
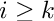
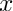
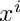
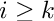
extract coefficients of for where is a variable of level 1

Returns

coefficients of for

See also

{getCoeffs (const CanonicalForm&, const int, const Variable& alpha), getCoeffs (const CanonicalForm&, const int)}

Parameters

[in]	G	compressed bivariate poly
[in]	k	some int
[in]	l	precision
[in]	degMipo	degree of minimal poly
[in]	alpha	algebraic variable
[in]	evaluation	evaluation point
[in]	M	bases change matrix

Definition at line 663 of file facFqBivarUtil.cc.

{
  ASSERT (G.isUnivariate() || G.inCoeffDomain(), "univariate input expected");
  CanonicalForm F= G (G.mvar() - evaluation, G.mvar());
  if (F.isZero())
    return CFArray ();
 
  Variable y= Variable (2);
  F= F (power (y, degMipo), y);
  F= F (y, alpha);
  zz_pX NTLF= convertFacCF2NTLzzpX (F);
  NTLF.rep.SetLength (l*degMipo);
  NTLF.rep= M*NTLF.rep;
  NTLF.normalize();
  F= convertNTLzzpX2CF (NTLF, y);
 
  if (degree (F, 2) < k)
    return CFArray();
 
  CFArray result= CFArray (degree (F) - k + 1);
 
  CFIterator j= F;
  for (int i= degree (F); i >= k; i--)
  {
    if (j.exp() == i)
    {
      result [i - k]= j.coeff();
      j++;
      if (!j.hasTerms())
        return result;
    }
    else
      result[i - k]= 0;
  }
  return result;
}

getCoeffs() [4/4]

CFArray getCoeffs	(	const CanonicalForm &	F,
		const int	k,
		const int	l,
		const int	degMipo,
		const Variable &	alpha,
		const CanonicalForm &	evaluation,
		const nmod_mat_t	M
	)

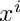
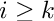
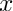
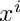
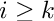
extract coefficients of for where is a variable of level 1

Returns

coefficients of for

See also

{getCoeffs (const CanonicalForm&, const int, const Variable& alpha), getCoeffs (const CanonicalForm&, const int)}

Parameters

[in]	G	compressed bivariate poly
[in]	k	some int
[in]	l	precision
[in]	degMipo	degree of minimal poly
[in]	alpha	algebraic variable
[in]	evaluation	evaluation point
[in]	M	bases change matrix

Definition at line 705 of file facFqBivarUtil.cc.

{
  ASSERT (G.isUnivariate() || G.inCoeffDomain(), "univariate input expected");
  CanonicalForm F= G (G.mvar() - evaluation, G.mvar());
  if (F.isZero())
    return CFArray ();
 
  Variable y= Variable (2);
  F= F (power (y, degMipo), y);
  F= F (y, alpha);
 
  nmod_poly_t FLINTF;
  nmod_mat_t MFLINTF, mulResult;
  nmod_mat_init (MFLINTF, l*degMipo, 1, getCharacteristic());
  nmod_mat_init (mulResult, l*degMipo, 1, getCharacteristic());
 
  convertFacCF2nmod_poly_t (FLINTF, F);
 
#ifndef slong
#define slong long
#endif
  slong i;
 
  for (i= 0; i < FLINTF->length; i++)
    nmod_mat_entry (MFLINTF, i, 0)= FLINTF->coeffs[i];
 
  for (; i < MFLINTF->r; i++)
    nmod_mat_entry (MFLINTF, i, 0)= 0;
 
  nmod_mat_mul (mulResult, M, MFLINTF);
 
  F= 0;
  for (i= 0; i < mulResult->r; i++)
    F += CanonicalForm ((long) nmod_mat_entry (mulResult, i, 0))*power (y, i);
 
  nmod_mat_clear (MFLINTF);
  nmod_mat_clear (mulResult);
  nmod_poly_clear(FLINTF);
 
  if (degree (F, 2) < k)
    return CFArray();
 
  CFArray result= CFArray (degree (F) - k + 1);
 
  CFIterator j= F;
  for (int i= degree (F); i >= k; i--)
  {
    if (j.exp() == i)
    {
      result [i - k]= j.coeff();
      j++;
      if (!j.hasTerms())
        return result;
    }
    else
      result[i - k]= 0;
  }
  return result;
}

GFInExtensionHelper()

static bool GFInExtensionHelper ( const CanonicalForm &  F, const int  number  )

inlinestatic

Definition at line 111 of file facFqBivarUtil.cc.

{
  if (F.isOne()) return false;
  InternalCF* buf;
  int exp;
  bool result= false;
  if (F.inBaseDomain())
  {
    buf= F.getval();
    exp= imm2int (buf);
    if (exp%number != 0)
      return true;
    else
      return result;
  }
  else
  {
    for (CFIterator i= F; i.hasTerms(); i++)
    {
      result= GFInExtensionHelper (i.coeff(), number);
      if (result == true)
        return result;
    }
  }
  return result;
}

indexUpdate()

void indexUpdate	(	int	index[],
		const int &	subsetSize,
		const int &	setSize,
		bool &	noSubset
	)

update index

Parameters

[in,out]	index	an array encoding a subset of size subsetSize
[in]	subsetSize	size of the subset
[in]	setSize	size of the given set
[in,out]	noSubset	if there is no subset we have not yet considered noSubset is true

Definition at line 373 of file facFqBivarUtil.cc.

{
  noSubset= false;
  if (subsetSize > setSize)
  {
    noSubset= true;
    return;
  }
  int * v= new int [setSize];
  for (int i= 0; i < setSize; i++)
    v[i]= index[i];
  if (subsetSize == 1)
  {
    v[0]= v[0] - 1;
    if (v[0] >= setSize)
    {
      noSubset= true;
      delete [] v;
      return;
    }
  }
  else
  {
    if (v[subsetSize - 1] - v[0] + 1 == subsetSize && v[0] > 1)
    {
      if (v[0] + subsetSize - 1 > setSize)
      {
        noSubset= true;
        delete [] v;
        return;
      }
      v[0]= v[0] - 1;
      for (int i= 1; i < subsetSize - 1; i++)
        v[i]= v[i - 1] + 1;
      v[subsetSize - 1]= v[subsetSize - 2];
    }
    else
    {
      if (v[0] + subsetSize - 1 > setSize)
      {
        noSubset= true;
        delete [] v;
        return;
      }
      for (int i= 1; i < subsetSize - 1; i++)
        v[i]= v[i - 1] + 1;
      v[subsetSize - 1]= v[subsetSize - 2];
    }
  }
  for (int i= 0; i < setSize; i++)
    index[i]= v[i];
  delete [] v;
}

isInExtension()

bool isInExtension	(	const CanonicalForm &	F,
		const CanonicalForm &	gamma,
		const int	k,
		const CanonicalForm &	delta,
		CFList &	source,
		CFList &	dest
	)

tests if F is not contained in a subfield defined by gamma (Fq case) or k (GF case)

Returns

isInExtension returns true if F is not contained in a subfield defined by gamma (Fq case) or k (GF case), false else

See also

appendTestMapDown()

Parameters

[in]	F	a poly over F_p (alpha)=Fq or GF(p^l)
[in]	gamma	a primitive element defining a subfield of Fq if we are not over some GF
	k	some int k such that k divides l if we are not over some Fq
[in]	delta	image of gamma
[in,out]	source	list of preimages
[in,out]	dest	list of images

Definition at line 184 of file facFqBivarUtil.cc.

{
  bool result;
  if (CFFactory::gettype() == GaloisFieldDomain)
  {
    int p= getCharacteristic();
    int orderFieldExtension= ipower (p, getGFDegree()) - 1;
    int order= ipower (p, k) - 1;
    int number= orderFieldExtension/order;
    result= GFInExtensionHelper (F, number);
    return result;
  }
  else
  {
    result= FqInExtensionHelper (F, gamma, delta, source, dest);
    return result;
  }
}

logarithmicDerivative() [1/2]

CFArray logarithmicDerivative	(	const CanonicalForm &	F,
		const CanonicalForm &	G,
		int	l,
		CanonicalForm &	Q
	)

compute the coefficients of the logarithmic derivative of G mod Variable (2)^l over Fq

Returns

an array of coefficients of the logarithmic derivative of G mod Variable (2)^l

Parameters

[in]	F	a bivariate poly
[in]	G	a factor of F
[in]	l	lifting precision
[in,out]	Q	F/G

Definition at line 459 of file facFqBivarUtil.cc.

{
  Variable x= Variable (2);
  Variable y= Variable (1);
  CanonicalForm xToL= power (x, l);
  CanonicalForm q,r;
  CanonicalForm logDeriv;
 
  TIMING_START (fac_log_deriv_div);
  q= newtonDiv (F, G, xToL);
  TIMING_END_AND_PRINT (fac_log_deriv_div, "time for division in logderiv1: ");
 
  TIMING_START (fac_log_deriv_mul);
  logDeriv= mulMod2 (q, deriv (G, y), xToL);
  TIMING_END_AND_PRINT (fac_log_deriv_mul, "time to multiply in logderiv1: ");
 
  if (degree (logDeriv, x) == 0)
  {
    Q= q;
    return CFArray();
  }
 
  int j= degree (logDeriv, y) + 1;
  CFArray result= CFArray (j);
  CFIterator ii;
  for (CFIterator i= logDeriv; i.hasTerms() && !logDeriv.isZero(); i++)
  {
    if (i.coeff().inCoeffDomain())
      result[0] += i.coeff()*power (x,i.exp());
    else
    {
      for (ii= i.coeff(); ii.hasTerms(); ii++)
        result[ii.exp()] += ii.coeff()*power (x,i.exp());
    }
  }
  Q= q;
  return result;
}

logarithmicDerivative() [2/2]

CFArray logarithmicDerivative	(	const CanonicalForm &	F,
		const CanonicalForm &	G,
		int	l,
		int	oldL,
		const CanonicalForm &	oldQ,
		CanonicalForm &	Q
	)

compute the coefficients of the logarithmic derivative of G mod Variable (2)^l over Fq with oldQ= F/G mod Variable (2)^oldL

Returns

an array of coefficients of the logarithmic derivative of G mod Variable (2)^l

Parameters

[in]	F	bivariate poly truncated at Variable(2)^l
[in]	G	a factor of F
[in]	l	lifting precision
[in]	oldL	old precision
[in]	oldQ	F/G mod Variable(2)^oldL
[in,out]	Q	F/G

Definition at line 501 of file facFqBivarUtil.cc.

{
  Variable x= Variable (2);
  Variable y= Variable (1);
  CanonicalForm xToL= power (x, l);
  CanonicalForm xToOldL= power (x, oldL);
  CanonicalForm xToLOldL= power (x, l-oldL);
  CanonicalForm q,r;
  CanonicalForm logDeriv;
 
  CanonicalForm bufF;
  TIMING_START (fac_log_deriv_pre);
  if ((oldL > 100 && l - oldL < 50) || (oldL < 100 && l - oldL < 30))
  {
    bufF= F;
    CanonicalForm oldF= mulMod2 (G, oldQ, xToL);
    bufF -= oldF;
    bufF= div (bufF, xToOldL);
  }
  else
  {
    //middle product style computation of [G*oldQ]^{l}_{oldL}
    CanonicalForm G3= div (G, xToOldL);
    CanonicalForm Up= mulMod2 (G3, oldQ, xToLOldL);
    CanonicalForm xToOldL2= power (x, (oldL+1)/2);
    CanonicalForm G2= mod (G, xToOldL);
    CanonicalForm G1= div (G2, xToOldL2);
    CanonicalForm G0= mod (G2, xToOldL2);
    CanonicalForm oldQ1= div (oldQ, xToOldL2);
    CanonicalForm oldQ0= mod (oldQ, xToOldL2);
    CanonicalForm Mid;
    if (oldL % 2 == 1)
      Mid= mulMod2 (G1, oldQ1*x, xToLOldL);
    else
      Mid= mulMod2 (G1, oldQ1, xToLOldL);
    //computation of Low might be faster using a real middle product?
    CanonicalForm Low= mulMod2 (G0, oldQ1, xToOldL)+mulMod2 (G1, oldQ0, xToOldL);
    Low= div (Low, power (x, oldL/2));
    Low= mod (Low, xToLOldL);
    Up += Mid + Low;
    bufF= div (F, xToOldL);
    bufF -= Up;
  }
  TIMING_END_AND_PRINT (fac_log_deriv_pre, "time to preprocess: ");
 
  TIMING_START (fac_log_deriv_div);
  if (l-oldL > 0)
    q= newtonDiv (bufF, G, xToLOldL);
  else
    q= 0;
  q *= xToOldL;
  q += oldQ;
  TIMING_END_AND_PRINT (fac_log_deriv_div, "time for div in logderiv2: ");
 
  TIMING_START (fac_log_deriv_mul);
  logDeriv= mulMod2 (q, deriv (G, y), xToL);
  TIMING_END_AND_PRINT (fac_log_deriv_mul, "time for mul in logderiv2: ");
 
  if (degree (logDeriv, x) == 0)
  {
    Q= q;
    return CFArray();
  }
 
  int j= degree (logDeriv,y) + 1;
  CFArray result= CFArray (j);
  CFIterator ii;
  for (CFIterator i= logDeriv; i.hasTerms() && !logDeriv.isZero(); i++)
  {
    if (i.coeff().inCoeffDomain())
      result[0] += i.coeff()*power (x,i.exp());
    else
    {
      for (ii= i.coeff(); ii.hasTerms(); ii++)
        result[ii.exp()] += ii.coeff()*power (x,i.exp());
    }
  }
  Q= q;
  return result;
}

mapDown()

CanonicalForm mapDown	(	const CanonicalForm &	F,
		const ExtensionInfo &	info,
		CFList &	source,
		CFList &	dest
	)

map a poly into a subfield of the current field, no testing is performed!

Returns

mapDown returns F mapped into a subfield of the current field

See also

appendTestMapDown(), appendMapDown()

Parameters

[in]	F	a poly
[in]	info	information about the sub- and current field
[in,out]	source	in case we are over some F_p (alpha) and want to map down into F_p (beta) source contains powers of the primitive element of F_p (alpha)
[in,out]	dest	as source but contains the corresponding powers of the primitive element of F_p (beta)

Definition at line 206 of file facFqBivarUtil.cc.

{
  int k= info.getGFDegree();
  Variable beta= info.getAlpha();
  CanonicalForm primElem= info.getGamma();
  CanonicalForm imPrimElem= info.getDelta();
  if (k > 1)
    return GFMapDown (F, k);
  else if (k == 1)
    return F;
  if (/*k==0 &&*/ beta == Variable (1))
    return F;
  else /*if (k==0 && beta != Variable (1))*/
    return mapDown (F, imPrimElem, primElem, beta, source, dest);
}

multiplicity()

CFFList multiplicity	(	CanonicalForm &	F,
		const CFList &	factors
	)

determine multiplicity of the factors

Returns

a list of factors of F with their multiplicity

Parameters

[in]	F	a poly
[in]	factors	a list of factors of F

Definition at line 436 of file facFqBivarUtil.cc.

{
  if (F.inCoeffDomain())
    return CFFList (CFFactor (F, 1));
  CFFList result;
  int multi= 0;
  CanonicalForm quot;
  for (CFListIterator i= factors; i.hasItem(); i++)
  {
    while (fdivides (i.getItem(), F, quot))
    {
      multi++;
      F= quot;
    }
    if (multi > 0)
      result.append (CFFactor (i.getItem(), multi));
    multi= 0;
  }
  return result;
}

normalize() [1/2]

void normalize

(

CFFList &

factors

)

as above

Parameters

[in,out]

factors

a list of factors

Definition at line 297 of file facFqBivarUtil.cc.

{
  CanonicalForm lcinv;
  for (CFFListIterator i= factors; i.hasItem(); i++)
  {
    lcinv= 1/ Lc (i.getItem().factor());
    i.getItem()= CFFactor (i.getItem().factor()*lcinv,
                           i.getItem().exp());
  }
  return;
}

normalize() [2/2]

void normalize

(

CFList &

factors

)

normalize factors, i.e. make factors monic

Parameters

[in,out]

factors

a list of polys

Definition at line 286 of file facFqBivarUtil.cc.

{
  CanonicalForm lcinv;
  for (CFListIterator i= factors; i.hasItem(); i++)
  {
    lcinv= 1/Lc (i.getItem());
    i.getItem() *= lcinv;
  }
  return;
}

recSubstituteCheck()

int recSubstituteCheck	(	const CanonicalForm &	F,
		const int	d
	)

Definition at line 1205 of file facFqBivarUtil.cc.

{
  if (F.inCoeffDomain())
    return 0;
  Variable x= Variable (1);
  if (degree (F, x) <= 1)
    return 0;
  CanonicalForm f= swapvar (F, F.mvar(), x);
  int sizef= 0;
  for (CFIterator i= f; i.hasTerms(); i++, sizef++)
  {
    if (i.exp() == 1)
      return 0;
  }
  int * expf= new int [sizef];
  int j= 0;
  for (CFIterator i= f; i.hasTerms(); i++, j++)
  {
    expf [j]= i.exp();
  }
 
  int indf= sizef - 1;
  if (expf[indf] == 0)
    indf--;
 
  if ((d%expf [indf] != 0 && expf[indf]%d != 0) || (expf[indf] == 1))
  {
    delete [] expf;
    return 0;
  }
 
  int result;
  if (d%expf [indf] == 0)
    result= expf[indf];
  else
    result= d;
  for (int i= indf - 1; i >= 0; i--)
  {
    if (expf [i]%result != 0)
    {
      delete [] expf;
      return 0;
    }
  }
 
  delete [] expf;
  return result;
}

reverseSubst() [1/2]

void reverseSubst	(	CFList &	L,
		const int	d,
		const Variable &	x
	)

reverse a substitution x^d->x

Parameters

[in,out]	L	a list of polys, returns the given list with x replaced by x^d
[in]	d	an integer > 0
[in]	x	a Variable

Definition at line 1309 of file facFqBivarUtil.cc.

{
  for (CFListIterator i= L; i.hasItem(); i++)
    i.getItem()= reverseSubst (i.getItem(), d, x);
}

reverseSubst() [2/2]

CanonicalForm reverseSubst	(	const CanonicalForm &	F,
		const int	d,
		const Variable &	x
	)

reverse a substitution x^d->x

Returns

a poly with x replaced by x^d

Parameters

[in]	F	a poly
[in]	d	an integer > 0
[in]	x	a Variable

Definition at line 1295 of file facFqBivarUtil.cc.

{
  if (d <= 1)
    return F;
  if (degree (F, x) <= 0)
    return F;
  CanonicalForm f= swapvar (F, x, F.mvar());
  CanonicalForm result= 0;
  for (CFIterator i= f; i.hasTerms(); i++)
    result += i.coeff()*power (f.mvar(), d*i.exp());
  return swapvar (result, x, F.mvar());
}

subset()

CFList subset	(	int	index[],
		const int &	s,
		const CFArray &	elements,
		bool &	noSubset
	)

extract a subset given by index of size s from elements, if there is no subset we have not yet considered noSubset is set to true. index encodes the next subset, e.g. if s= 3, elements= {a,b,c,d}, index= {1, 2, 4, 0}, then subset= {a,c,d}. index is of size elements.size().

Returns

subset returns a list of polys of length s if there is a subset we have not yet considered.

Parameters

[in,out]	index	an array encoding the next subset
[in]	s	size of the subset
[in]	elements	an array of polys
[in,out]	noSubset	if there is no subset we have not yet considered noSubset is true

Definition at line 309 of file facFqBivarUtil.cc.

{
  int r= elements.size();
  int i= 0;
  CFList result;
  noSubset= false;
  if (index[s - 1] == 0)
  {
    while (i < s)
    {
      index[i]= i + 1;
      result.append (elements[i]);
      i++;
    }
    return result;
  }
  int buf;
  int k;
  bool found= false;
  if (index[s - 1] == r)
  {
    if (index[0] == r - s + 1)
    {
      noSubset= true;
      return result;
    }
    else {
      while (found == false)
      {
        if (index[s - 2 - i] < r - i - 1)
          found= true;
        i++;
      }
      buf= index[s - i - 1];
      k= 0;
      while (s - i - 1 + k < s)
      {
        index[s - i - 1 + k]= buf + k + 1;
        k++;
      }
    }
    for (int j= 0; j < s; j++)
      result.append (elements[index[j] - 1]);
    return result;
  }
  else
  {
    index[s - 1] += 1;
    for (int j= 0; j < s; j++)
      result.append (elements[index[j] - 1]);
    return result;
  }
}

subsetDegree()

int subsetDegree

(

const CFList &

S

)

compute the sum of degrees in Variable(1) of elements in S

Returns

subsetDegree returns the sum of degrees in Variable(1) of elements in S

Parameters

[in]

S

a list of polys

Definition at line 428 of file facFqBivarUtil.cc.

{
  int result= 0;
  for (CFListIterator i= S; i.hasItem(); i++)
    result += degree (i.getItem(), Variable (1));
  return result;
}

subst()

void subst	(	const CanonicalForm &	F,
		CanonicalForm &	A,
		const int	d,
		const Variable &	x
	)

substitute x^d by x in F

Parameters

[in]	F	a polynomial
[in,out]	A	returns F with x^d replaced by x
	d	d > 1 such that a substitution x^d -> x [in] is possible
[in]	x	a Variable

Definition at line 1275 of file facFqBivarUtil.cc.

{
  if (d <= 1)
  {
    A= F;
    return;
  }
  if (degree (F, x) <= 0)
  {
    A= F;
    return;
  }
  CanonicalForm C= 0;
  CanonicalForm f= swapvar (F, x, F.mvar());
  for (CFIterator i= f; i.hasTerms(); i++)
    C += i.coeff()*power (f.mvar(), i.exp()/ d);
  A= swapvar (C, x, F.mvar());
}

substituteCheck() [1/3]

static int substituteCheck ( const CanonicalForm &  F, const CanonicalForm &  G  )

static

Definition at line 1126 of file facFqBivarUtil.cc.

{
  if (F.inCoeffDomain() || G.inCoeffDomain())
    return 0;
  Variable x= Variable (1);
  if (degree (F, x) <= 1 || degree (G, x) <= 1)
    return 0;
  CanonicalForm f= swapvar (F, F.mvar(), x);
  CanonicalForm g= swapvar (G, G.mvar(), x);
  int sizef= 0;
  int sizeg= 0;
  for (CFIterator i= f; i.hasTerms(); i++, sizef++)
  {
    if (i.exp() == 1)
      return 0;
  }
  for (CFIterator i= g; i.hasTerms(); i++, sizeg++)
  {
    if (i.exp() == 1)
      return 0;
  }
  int * expf= new int [sizef];
  int * expg= new int [sizeg];
  int j= 0;
  for (CFIterator i= f; i.hasTerms(); i++, j++)
  {
    expf [j]= i.exp();
  }
  j= 0;
  for (CFIterator i= g; i.hasTerms(); i++, j++)
  {
    expg [j]= i.exp();
  }
 
  int indf= sizef - 1;
  int indg= sizeg - 1;
  if (expf[indf] == 0)
    indf--;
  if (expg[indg] == 0)
    indg--;
 
  if ((expg[indg]%expf [indf] != 0 && expf[indf]%expg[indg] != 0) ||
      (expg[indg] == 1 && expf[indf] == 1))
  {
    delete [] expg;
    delete [] expf;
    return 0;
  }
 
  int result;
  if (expg [indg]%expf [indf] == 0)
    result= expf[indf];
  else
    result= expg[indg];
  for (int i= indf - 1; i >= 0; i--)
  {
    if (expf [i]%result != 0)
    {
      delete [] expf;
      delete [] expg;
      return 0;
    }
  }
 
  for (int i= indg - 1; i >= 0; i--)
  {
    if (expg [i]%result != 0)
    {
      delete [] expf;
      delete [] expg;
      return 0;
    }
  }
 
  delete [] expg;
  delete [] expf;
  return result;
}

substituteCheck() [2/3]

int substituteCheck	(	const CanonicalForm &	F,
		const Variable &	x
	)

check if a substitution x^n->x is possible

Returns

an integer n > 1, if a substitution described as above is possible else n <= 1

Parameters

[in]	F	a polynomial
[in]	x	some variable

Definition at line 1089 of file facFqBivarUtil.cc.

{
  if (F.inCoeffDomain())
    return 0;
  if (degree (F, x) < 0)
    return 0;
  CanonicalForm f= swapvar (F, F.mvar(), x);
  int sizef= 0;
  for (CFIterator i= f; i.hasTerms(); i++, sizef++)
  {
    if (i.exp() == 1)
      return 0;
  }
  int * expf= new int [sizef];
  int j= 0;
  for (CFIterator i= f; i.hasTerms(); i++, j++)
    expf [j]= i.exp();
 
  int indf= sizef - 1;
  if (expf[indf] == 0)
    indf--;
 
  int result= expf[indf];
  for (int i= indf - 1; i >= 0; i--)
  {
    if (expf [i]%result != 0)
    {
      delete [] expf;
      return 0;
    }
  }
 
  delete [] expf;
  return result;
}

substituteCheck() [3/3]

int substituteCheck

(

const CFList &

L

)

checks if a substitution x^n->x is possible

Returns

an integer n > 1, if a substitution described as above is possible else n <= 1

Parameters

[in]

L

a list of univariate polys

Definition at line 1254 of file facFqBivarUtil.cc.

{
  ASSERT (L.length() > 1, "expected a list of at least two elements");
  if (L.length() < 2)
    return 0;
  CFListIterator i= L;
  i++;
  int result= substituteCheck (L.getFirst(), i.getItem());
  if (result <= 1)
    return result;
  i++;
  for (;i.hasItem(); i++)
  {
    result= recSubstituteCheck (i.getItem(), result);
    if (result <= 1)
      return result;
  }
  return result;
}

swapDecompress()

void swapDecompress	(	CFList &	factors,
		const bool	swap,
		const CFMap &	N
	)

swap Variables in factors, then decompress factors

Parameters

[in,out]	factors	a list of polys
[in]	swap	indicates the need to swap
[in]	N	a map

Definition at line 97 of file facFqBivarUtil.cc.

{
  Variable x= Variable (1);
  Variable y= Variable (2);
  for (CFListIterator i= factors; i.hasItem(); i++)
  {
    if (swap)
      i.getItem()= swapvar (i.getItem(), x, y);
    i.getItem()= N (i.getItem());
  }
  return;
}

TIMING_DEFINE_PRINT()

TIMING_DEFINE_PRINT

(

fac_log_deriv_div

)

&

writeInMatrix()

void writeInMatrix	(	CFMatrix &	M,
		const CFArray &	A,
		const int	column,
		const int	startIndex
	)

write A into M starting at row startIndex

Parameters

[in,out]	M	some matrix
[in]	A	array of polys
[in]	column	column in which A is written
[in]	startIndex	row in which to start

Definition at line 586 of file facFqBivarUtil.cc.

{
  ASSERT (A.size () - startIndex >= 0, "wrong starting index");
  ASSERT (A.size () - startIndex <= M.rows(), "wrong starting index");
  ASSERT (column > 0 && column <= M.columns(), "wrong column");
  if (A.size() - startIndex <= 0) return;
  int j= 1;
  for (int i= startIndex; i < A.size(); i++, j++)
    M (j, column)= A [i];
}

Variable Documentation

factors2

const CFList& factors2

Initial value:

{
  for (CFListIterator i= factors2; i.hasItem(); i++)
  {
    if (!i.getItem().inCoeffDomain())
      factors1.append (i.getItem());
  }
  return

Definition at line 41 of file facFqBivarUtil.cc.