facBivar.h File Reference

bivariate factorization over Q(a) More...

#include "cf_assert.h"
#include "timing.h"
#include "facFqBivarUtil.h"
#include "DegreePattern.h"
#include "cf_util.h"
#include "facFqSquarefree.h"
#include "cf_map.h"
#include "cf_algorithm.h"
#include "cfNewtonPolygon.h"
#include "fac_util.h"

Go to the source code of this file.

Functions
	TIMING_DEFINE_PRINT (fac_bi_sqrf) TIMING_DEFINE_PRINT(fac_bi_factor_sqrf) CFList biFactorize(const CanonicalForm &F
CFList	ratBiSqrfFactorize (const CanonicalForm &G, const Variable &v=Variable(1))
	factorize a squarefree bivariate polynomial over . More...
CFFList	ratBiFactorize (const CanonicalForm &G, const Variable &v=Variable(1), bool substCheck=true)
	factorize a bivariate polynomial over More...
CFList	conv (const CFFList &L)
	convert a CFFList to a CFList by dropping the multiplicity More...
modpk	coeffBound (const CanonicalForm &f, int p, const CanonicalForm &mipo)
	compute p^k larger than the bound on the coefficients of a factor of f over Q (mipo) More...
void	findGoodPrime (const CanonicalForm &f, int &start)
	find a big prime p from our tables such that no term of f vanishes mod p More...
modpk	coeffBound (const CanonicalForm &f, int p)
	compute p^k larger than the bound on the coefficients of a factor of f over Z More...

Variables
const Variable &	v
	< [in] a sqrfree bivariate poly More...

Detailed Description

bivariate factorization over Q(a)

Author

Martin Lee

Definition in file facBivar.h.

Function Documentation

coeffBound() [1/2]

modpk coeffBound	(	const CanonicalForm &	f,
		int	p
	)

compute p^k larger than the bound on the coefficients of a factor of f over Z

Parameters

[in]	f	poly over Z
[in]	p	some positive integer

coeffBound() [2/2]

modpk coeffBound	(	const CanonicalForm &	f,
		int	p,
		const CanonicalForm &	mipo
	)

compute p^k larger than the bound on the coefficients of a factor of f over Q (mipo)

Parameters

[in]	f	poly over Z[a]
[in]	p	some positive integer
[in]	mipo	minimal polynomial with denominator 1

Definition at line 97 of file facBivar.cc.

{
    int * degs = degrees( f );
    int M = 0, i, k = f.level();
    CanonicalForm K= 1;
    for ( i = 1; i <= k; i++ )
    {
        M += degs[i];
        K *= degs[i] + 1;
    }
    DELETE_ARRAY(degs);
    K /= power (CanonicalForm (2), k/2);
    K *= power (CanonicalForm (2), M);
    int N= degree (mipo);
    CanonicalForm b;
    b= 2*power (maxNorm (f), N)*power (maxNorm (mipo), 4*N)*K*
       power (CanonicalForm (2), N)*
       power (CanonicalForm (N+1), 4*N);
    b /= power (abs (lc (mipo)), N);
 
    CanonicalForm B = p;
    k = 1;
    while ( B < b ) {
        B *= p;
        k++;
    }
    return modpk( p, k );
}

conv()

CFList conv

(

const CFFList &

L

)

convert a CFFList to a CFList by dropping the multiplicity

Parameters

[in]

L

a CFFList

Definition at line 126 of file facBivar.cc.

{
  CFList result;
  for (CFFListIterator i= L; i.hasItem(); i++)
    result.append (i.getItem().factor());
  return result;
}

findGoodPrime()

void findGoodPrime	(	const CanonicalForm &	f,
		int &	start
	)

find a big prime p from our tables such that no term of f vanishes mod p

Parameters

[in]	f	poly over Z or Z[a]
[in,out]	start	index of big prime in cf_primetab.h

Definition at line 61 of file facBivar.cc.

{
  if (! f.inBaseDomain() )
  {
    CFIterator i = f;
    for(;;)
    {
      if  ( i.hasTerms() )
      {
        findGoodPrime(i.coeff(),start);
        if (0==cf_getBigPrime(start)) return;
        if((i.exp()!=0) && ((i.exp() % cf_getBigPrime(start))==0))
        {
          start++;
          i=f;
        }
        else  i++;
      }
      else break;
    }
  }
  else
  {
    if (f.inZ())
    {
      if (0==cf_getBigPrime(start)) return;
      while((!f.isZero()) && (mod(f,cf_getBigPrime(start))==0))
      {
        start++;
        if (0==cf_getBigPrime(start)) return;
      }
    }
  }
}

ratBiFactorize()

CFFList ratBiFactorize ( const CanonicalForm &  G, const Variable &  v = Variable (1), bool  substCheck = true  )

inline

factorize a bivariate polynomial over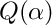

Returns

ratBiFactorize returns a list of monic factors with multiplicity, the first element is the leading coefficient.

Parameters

[in]	G	a bivariate poly
[in]	v	algebraic variable
[in]	substCheck	enables substitute check

Definition at line 129 of file facBivar.h.

{
  CFMap N;
  CanonicalForm F= compress (G, N);
 
  if (substCheck)
  {
    bool foundOne= false;
    int * substDegree= new int [F.level()];
    for (int i= 1; i <= F.level(); i++)
    {
      substDegree[i-1]= substituteCheck (F, Variable (i));
      if (substDegree [i-1] > 1)
      {
        foundOne= true;
        subst (F, F, substDegree[i-1], Variable (i));
      }
    }
    if (foundOne)
    {
      CFFList result= ratBiFactorize (F, v, false);
      CFFList newResult, tmp;
      CanonicalForm tmp2;
      newResult.insert (result.getFirst());
      result.removeFirst();
      for (CFFListIterator i= result; i.hasItem(); i++)
      {
        tmp2= i.getItem().factor();
        for (int j= 1; j <= F.level(); j++)
        {
          if (substDegree[j-1] > 1)
            tmp2= reverseSubst (tmp2, substDegree[j-1], Variable (j));
        }
        tmp= ratBiFactorize (tmp2, v, false);
        tmp.removeFirst();
        for (CFFListIterator j= tmp; j.hasItem(); j++)
          newResult.append (CFFactor (j.getItem().factor(),
                                      j.getItem().exp()*i.getItem().exp()));
      }
      decompress (newResult, N);
      delete [] substDegree;
      return newResult;
    }
    delete [] substDegree;
  }
 
  CanonicalForm LcF= Lc (F);
  CanonicalForm contentX= content (F, 1);
  CanonicalForm contentY= content (F, 2);
  F /= (contentX*contentY);
  CFFList contentXFactors, contentYFactors;
  if (v.level() != 1)
  {
    contentXFactors= factorize (contentX, v);
    contentYFactors= factorize (contentY, v);
  }
  else
  {
    contentXFactors= factorize (contentX);
    contentYFactors= factorize (contentY);
  }
  if (contentXFactors.getFirst().factor().inCoeffDomain())
    contentXFactors.removeFirst();
  if (contentYFactors.getFirst().factor().inCoeffDomain())
    contentYFactors.removeFirst();
  decompress (contentXFactors, N);
  decompress (contentYFactors, N);
  CFFList result, resultRoot;
  if (F.inCoeffDomain())
  {
    result= Union (contentXFactors, contentYFactors);
    if (isOn (SW_RATIONAL))
    {
      normalize (result);
      if (v.level() == 1)
      {
        for (CFFListIterator i= result; i.hasItem(); i++)
        {
          LcF /= power (bCommonDen (i.getItem().factor()), i.getItem().exp());
          i.getItem()= CFFactor (i.getItem().factor()*
                       bCommonDen(i.getItem().factor()), i.getItem().exp());
        }
      }
      result.insert (CFFactor (LcF, 1));
    }
    return result;
  }
 
  mpz_t * M=new mpz_t [4];
  mpz_init (M[0]);
  mpz_init (M[1]);
  mpz_init (M[2]);
  mpz_init (M[3]);
 
  mpz_t * S=new mpz_t [2];
  mpz_init (S[0]);
  mpz_init (S[1]);
 
  F= compress (F, M, S);
  TIMING_START (fac_bi_sqrf);
  CFFList sqrfFactors= sqrFree (F);
  TIMING_END_AND_PRINT (fac_bi_sqrf,
                       "time for bivariate sqrf factors over Q: ");
  for (CFFListIterator i= sqrfFactors; i.hasItem(); i++)
  {
    TIMING_START (fac_bi_factor_sqrf);
    CFList tmp= ratBiSqrfFactorize (i.getItem().factor(), v);
    TIMING_END_AND_PRINT (fac_bi_factor_sqrf,
                          "time to factor bivariate sqrf factors over Q: ");
    for (CFListIterator j= tmp; j.hasItem(); j++)
    {
      if (j.getItem().inCoeffDomain()) continue;
      result.append (CFFactor (N (decompress (j.getItem(), M, S)),
                               i.getItem().exp()));
    }
  }
  result= Union (result, contentXFactors);
  result= Union (result, contentYFactors);
  if (isOn (SW_RATIONAL))
  {
    normalize (result);
    if (v.level() == 1)
    {
      for (CFFListIterator i= result; i.hasItem(); i++)
      {
        LcF /= power (bCommonDen (i.getItem().factor()), i.getItem().exp());
        i.getItem()= CFFactor (i.getItem().factor()*
                     bCommonDen(i.getItem().factor()), i.getItem().exp());
      }
    }
    result.insert (CFFactor (LcF, 1));
  }
 
  mpz_clear (M[0]);
  mpz_clear (M[1]);
  mpz_clear (M[2]);
  mpz_clear (M[3]);
  delete [] M;
 
  mpz_clear (S[0]);
  mpz_clear (S[1]);
  delete [] S;
 
  return result;
}

ratBiSqrfFactorize()

CFList ratBiSqrfFactorize ( const CanonicalForm &  G, const Variable &  v = Variable (1)  )

inline

factorize a squarefree bivariate polynomial over .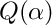

@ return ratBiSqrfFactorize returns a list of monic factors, the first element is the leading coefficient.

Parameters

[in]	G	a bivariate poly
[in]	v	algebraic variable

Definition at line 47 of file facBivar.h.

{
  CFMap N;
  CanonicalForm F= compress (G, N);
  CanonicalForm contentX= content (F, 1); //erwarte hier primitiven input: primitiv über Z bzw. Z[a]
  CanonicalForm contentY= content (F, 2);
  F /= (contentX*contentY);
  CFFList contentXFactors, contentYFactors;
  if (v.level() != 1)
  {
    contentXFactors= factorize (contentX, v);
    contentYFactors= factorize (contentY, v);
  }
  else
  {
    contentXFactors= factorize (contentX);
    contentYFactors= factorize (contentY);
  }
  if (contentXFactors.getFirst().factor().inCoeffDomain())
    contentXFactors.removeFirst();
  if (contentYFactors.getFirst().factor().inCoeffDomain())
    contentYFactors.removeFirst();
  if (F.inCoeffDomain())
  {
    CFList result;
    for (CFFListIterator i= contentXFactors; i.hasItem(); i++)
      result.append (N (i.getItem().factor()));
    for (CFFListIterator i= contentYFactors; i.hasItem(); i++)
      result.append (N (i.getItem().factor()));
    if (isOn (SW_RATIONAL))
    {
      normalize (result);
      result.insert (Lc (G));
    }
    return result;
  }
 
  mpz_t * M=new mpz_t [4];
  mpz_init (M[0]);
  mpz_init (M[1]);
  mpz_init (M[2]);
  mpz_init (M[3]);
 
  mpz_t * S=new mpz_t [2];
  mpz_init (S[0]);
  mpz_init (S[1]);
 
  F= compress (F, M, S);
  CFList result= biFactorize (F, v);
  for (CFListIterator i= result; i.hasItem(); i++)
    i.getItem()= N (decompress (i.getItem(), M, S));
  for (CFFListIterator i= contentXFactors; i.hasItem(); i++)
    result.append (N(i.getItem().factor()));
  for (CFFListIterator i= contentYFactors; i.hasItem(); i++)
    result.append (N (i.getItem().factor()));
  if (isOn (SW_RATIONAL))
  {
    normalize (result);
    result.insert (Lc (G));
  }
 
  mpz_clear (M[0]);
  mpz_clear (M[1]);
  mpz_clear (M[2]);
  mpz_clear (M[3]);
  delete [] M;
 
  mpz_clear (S[0]);
  mpz_clear (S[1]);
  delete [] S;
 
  return result;
}

TIMING_DEFINE_PRINT()

TIMING_DEFINE_PRINT

(

fac_bi_sqrf

)

const &

Returns

biFactorize returns a list of factors of F. If F is not monic its leading coefficient is not outputted.

Variable Documentation

v

const Variable& v

< [in] a sqrfree bivariate poly

< [in] some algebraic variable

Definition at line 38 of file facBivar.h.