 |
My Project
|
 |
My Project
|
Factorization over algebraic function fields. More...
#include "canonicalform.h"Go to the source code of this file.
Functions | |
| CanonicalForm | alg_gcd (const CanonicalForm &, const CanonicalForm &, const CFList &) |
| CFFList | facAlgFunc2 (const CanonicalForm &f, const CFList &as) |
| factorize a polynomial f that is irreducible over the ground field modulo an extension given by an irreducible characteristic set as, f is assumed to be integral, i.e. | |
| CFFList | facAlgFunc (const CanonicalForm &f, const CFList &as) |
| factorize a polynomial f modulo an extension given by an irreducible characteristic set as, f is assumed to be integral, i.e. | |
Factorization over algebraic function fields.
Definition in file facAlgFunc.h.
| CanonicalForm alg_gcd | ( | const CanonicalForm & | fff, |
| const CanonicalForm & | ggg, | ||
| const CFList & | as | ||
| ) |
Definition at line 61 of file facAlgFunc.cc.
| CFFList facAlgFunc | ( | const CanonicalForm & | f, |
| const CFList & | as | ||
| ) |
factorize a polynomial f modulo an extension given by an irreducible characteristic set as, f is assumed to be integral, i.e. ![$ f\in K[x_1,\ldots,x_n]/(as) $](form_32.png)
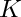
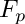
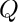
factorize a polynomial f modulo an extension given by an irreducible characteristic set as, f is assumed to be integral, i.e. ![$ f\in K[x_1,\ldots,x_n]/(as) $](form_32.png)
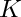
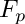
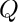
| [in] | f | univariate poly |
| [in] | as | irreducible characteristic set |
Definition at line 1043 of file facAlgFunc.cc.
| CFFList facAlgFunc2 | ( | const CanonicalForm & | f, |
| const CFList & | as | ||
| ) |
factorize a polynomial f that is irreducible over the ground field modulo an extension given by an irreducible characteristic set as, f is assumed to be integral, i.e. ![$ f\in K[x_1,\ldots,x_n]/(as) $](form_32.png)
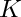
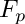
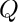
factorize a polynomial f that is irreducible over the ground field modulo an extension given by an irreducible characteristic set as, f is assumed to be integral, i.e. ![$ f\in K[x_1,\ldots,x_n]/(as) $](form_32.png)
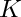
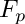
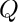
| [in] | f | univariate poly |
| [in] | as | irreducible characteristic set |
Definition at line 905 of file facAlgFunc.cc.