 |
My Project
|
 |
My Project
|
This file provides functions to factorize polynomials over alg. More...
#include "config.h"#include "cf_assert.h"#include "debug.h"#include "cf_generator.h"#include "cf_iter.h"#include "cf_util.h"#include "cf_algorithm.h"#include "templates/ftmpl_functions.h"#include "cf_map.h"#include "cfModResultant.h"#include "cfCharSets.h"#include "facAlgFunc.h"#include "facAlgFuncUtil.h"Go to the source code of this file.
Functions | |
| void | out_cf (const char *s1, const CanonicalForm &f, const char *s2) |
| cf_algorithm.cc - simple mathematical algorithms. More... | |
| CanonicalForm | alg_content (const CanonicalForm &f, const CFList &as) |
| CanonicalForm | alg_gcd (const CanonicalForm &fff, const CanonicalForm &ggg, const CFList &as) |
| static CanonicalForm | resultante (const CanonicalForm &f, const CanonicalForm &g, const Variable &v) |
| static CFFList | norm (const CanonicalForm &f, const CanonicalForm &PPalpha, CFGenerator &myrandom, CanonicalForm &s, CanonicalForm &g, CanonicalForm &R, bool proof) |
| compute the norm R of f over PPalpha, g= f (x-s*alpha) if proof==true, R is squarefree and if in addition getCharacteristic() > 0 the squarefree factors of R are returned. Based on Trager's sqrf_norm algorithm. More... | |
| static CFFList | sqrfNorm (const CanonicalForm &f, const CanonicalForm &PPalpha, const Variable &Extension, CanonicalForm &s, CanonicalForm &g, CanonicalForm &R) |
| see norm, R is guaranteed to be squarefree Based on Trager's sqrf_norm algorithm. More... | |
| static CFList | simpleExtension (CFList &backSubst, const CFList &Astar, const Variable &Extension, bool &isFunctionField, CanonicalForm &R) |
| static CFFList | Trager (const CanonicalForm &F, const CFList &Astar, const Variable &vminpoly, const CFList &as, bool isFunctionField) |
| Trager's algorithm, i.e. convert to one field extension and factorize over this field extension. More... | |
| CFList | mapIntoPIE (CFFList &varsMapLevel, CanonicalForm &lcmVars, const CFList &AS) |
| map elements in AS into a PIE | |
| CFFList | SteelTrager (const CanonicalForm &f, const CFList &AS) |
| algorithm of A. Steel described in "Conquering Inseparability: Primary
decomposition and multivariate factorization over algebraic function fields
of positive characteristic" with the following modifications: we use characteristic sets in IdealOverSubfield and Trager's primitive element algorithm instead of FGLM More... | |
| CFFList | facAlgFunc2 (const CanonicalForm &f, const CFList &as) |
| factorize a polynomial that is irreducible over the ground field modulo an extension given by an irreducible characteristic set More... | |
| CFFList | facAlgFunc (const CanonicalForm &f, const CFList &as) |
| factorize a polynomial modulo an extension given by an irreducible characteristic set More... | |
This file provides functions to factorize polynomials over alg.
function fields
ABSTRACT: Descriptions can be found in B. Trager "Algebraic Factoring and Rational Function Integration" and A. Steel "Conquering Inseparability: Primary decomposition and multivariate factorization over algebraic function fields of positive characteristic"
Definition in file facAlgFunc.cc.
| CanonicalForm alg_content | ( | const CanonicalForm & | f, |
| const CFList & | as | ||
| ) |
Definition at line 42 of file facAlgFunc.cc.
| CanonicalForm alg_gcd | ( | const CanonicalForm & | fff, |
| const CanonicalForm & | ggg, | ||
| const CFList & | as | ||
| ) |
Definition at line 61 of file facAlgFunc.cc.
| CFFList facAlgFunc | ( | const CanonicalForm & | f, |
| const CFList & | as | ||
| ) |
factorize a polynomial modulo an extension given by an irreducible characteristic set
factorize a polynomial f modulo an extension given by an irreducible characteristic set as, f is assumed to be integral, i.e. ![$ f\in K[x_1,\ldots,x_n]/(as) $](form_32.png)
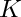
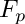
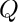
| [in] | f | univariate poly |
| [in] | as | irreducible characteristic set |
Definition at line 1043 of file facAlgFunc.cc.
| CFFList facAlgFunc2 | ( | const CanonicalForm & | f, |
| const CFList & | as | ||
| ) |
factorize a polynomial that is irreducible over the ground field modulo an extension given by an irreducible characteristic set
factorize a polynomial f that is irreducible over the ground field modulo an extension given by an irreducible characteristic set as, f is assumed to be integral, i.e. ![$ f\in K[x_1,\ldots,x_n]/(as) $](form_32.png)
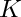
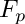
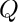
| [in] | f | univariate poly |
| [in] | as | irreducible characteristic set |
Definition at line 905 of file facAlgFunc.cc.
| CFList mapIntoPIE | ( | CFFList & | varsMapLevel, |
| CanonicalForm & | lcmVars, | ||
| const CFList & | AS | ||
| ) |
map elements in AS into a PIE 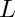
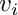
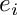
![$ L=K(\sqrt[p^{e_1}]{v_1}, \ldots, \sqrt[p^{e_n}]{v_n}) $](form_31.png)
Definition at line 609 of file facAlgFunc.cc.
|
static |
compute the norm R of f over PPalpha, g= f (x-s*alpha) if proof==true, R is squarefree and if in addition getCharacteristic() > 0 the squarefree factors of R are returned. Based on Trager's sqrf_norm algorithm.
Definition at line 206 of file facAlgFunc.cc.
| void out_cf | ( | const char * | s1, |
| const CanonicalForm & | f, | ||
| const char * | s2 | ||
| ) |
cf_algorithm.cc - simple mathematical algorithms.
Hierarchy: mathematical algorithms on canonical forms
A "mathematical" algorithm is an algorithm which calculates some mathematical function in contrast to a "structural" algorithm which gives structural information on polynomials.
Compare these functions to the functions in ‘cf_ops.cc’, which are structural algorithms.
Definition at line 99 of file cf_factor.cc.
|
static |
Definition at line 179 of file facAlgFunc.cc.
|
static |
Definition at line 313 of file facAlgFunc.cc.
|
static |
see norm, R is guaranteed to be squarefree Based on Trager's sqrf_norm algorithm.
Definition at line 287 of file facAlgFunc.cc.
| CFFList SteelTrager | ( | const CanonicalForm & | f, |
| const CFList & | AS | ||
| ) |
algorithm of A. Steel described in "Conquering Inseparability: Primary decomposition and multivariate factorization over algebraic function fields of positive characteristic" with the following modifications: we use characteristic sets in IdealOverSubfield and Trager's primitive element algorithm instead of FGLM
Definition at line 759 of file facAlgFunc.cc.
|
static |
Trager's algorithm, i.e. convert to one field extension and factorize over this field extension.
Definition at line 430 of file facAlgFunc.cc.